INTRODUCCIÓN
El flujo simultáneo de dos y tres fases, es un fenómeno que suele presentarse a lo largo de la vida de productiva de los yacimientos de hidrocarburos, tanto en su etapa de explotación primaria, como en las etapas de recobro secundario y mejorado, donde se evidencia con mayor frecuencia.
El conocimiento de las permeabilidades relativas es fundamental para el correcto modelado de este fenómeno, por esto, diversas metodologías experimentales han sido propuestas para la estimación de esta propiedad. Dentro de estas, las que involucran el uso de experimentos de inyección de fluidos en estado no-estacionario son frecuentemente usadas, debido al poco tiempo que requieren para su ejecución. La información obtenida de estos ensayos se analiza e interpreta para estimar cuales son las permeabilidades relativas que reproducen el comportamiento observado en el laboratorio.
Aunque la estimación de permeabilidades relativas para los casos de dos fases ha sido ampliamente estudiada, menores esfuerzos se realizan para estimar el comportamiento de esta propiedad en los casos de flujo de tres fases, principalmente, por la dificultad existente para interpretar la información experimental obtenida. El presente trabajo expone el desarrollo de una nueva metodología para la determinación experimental de las permeabilidades relativas de dos y tres fases por medio del enfoque de ajuste histórico. Un algoritmo para el ajuste automático es propuesto y se valida por medio de su aplicación con datos experimentales.
DESARROLLO DEL
ALGORITMO PARA
ESTIMACIÓN DE
PERMEABILIDADES
RELATIVAS POR AJUSTE
HISTÓRICO AUTOMÁTICO
Para el desarrollo del algoritmo de estimación, es necesaria la implementación de un código de simulación numérica del experimento, y uno de optimización numérica, el cual permite el ajuste automático de esta simulación con la información experimental.
De acuerdo con lo anterior, las permeabilidades relativas deben definirse como funciones de las saturaciones de las fases, de manera, que el ajuste entre lo simulado y lo observado se busca cambiando los parámetros de dichas funciones. Como se menciona en trabajos previos (Helset, Norvdtvedt, Skjæveland y Virnovsky, 1998) (Nordtvedt, et al., 1997), las representaciones funcionales seleccionadas para describir las permeabilidades relativas, son importantes debido a que definen, el número de parámetros a usar para buscar el ajuste, y la flexibilidad que tienen las curvas y superficies a estimar. Un número mayor de parámetros, generalmente, permite mayor flexibilidad para que las curvas puedan describir mejor las permeabilidades relativas, pero incrementa el número de variables a optimizar y por lo tanto los tiempos de computo (Kreig y Watson, 1986).
Para este caso, en el sistema de dos fases se propone usar el modelo propuesto por Corey (Corey, 1954) (Brooks y Corey, 1964), el cual representa la permeabilidad relativa como una potencia de las saturación normalizada, tal como se muestra en las ecuaciones de la (1) a la (3).
Donde:
· Krow es la permeabilidad relativa del aceite en el sistema agua-aceite
· Krw es la permeabilidad relativa del agua
· Krg es la permeabilidad relativa del gas • Sw es la saturación de agua
· Swc es la saturación de agua irreducible
· Sorw es la saturación residual de aceite
Para el sistema de tres fases se debe definir una función con parámetros ajustables para describir la permeabilidad relativa. Para este caso, se propone una modificación del modelo de Stone II (Stone, 1970), en la cual se agregan dos exponentes que actúan cómo parámetros de ajuste de estas superficies. El modelo propuesto se muestra en la ecuación (4).
Donde,
· Kro* es la permeabilidad relativa máxima del aceite
· ( medida a saturación de agua irreducible )
· Krog es la permeabilidad relativa del aceite en el sistema gas-aceite
· Krg es la permeabilidad relativa del gas
· t1 y t2 son los parámetros de ajuste agregados
Similarmente, una modificación a la curva de permeabilidad relativa del agua es propuesta para el caso en el cual el gas se encuentra en el medio poroso. El enfoque propuesto asume que la presencia de gas puede afectar la saturación irreducible de agua, y por lo tanto el rango móvil de fluidos, para modelar esto, se toma como nuevo parámetro la saturación de agua irreducible al gas (Swcg), con esta nueva información, se escala la curva de permeabilidad relativa del agua conocida del sistema agua-aceite, para obtener su equivalente en el sistema tres fases, por medio de la ecuación (5).
ALGORITMO DE SIMULACIÓN DE LOS EXPERIMENTOS
Para aplicar el enfoque de ajuste histórico, es necesaria la simulación de los experimentos realizados, con este fin, se desarrolla un motor numérico en Matlab especializado en coreflooding, el cual modela flujo multifásico (tres fases) unidimensional, de fluidos totalmente inmiscibles, en una roca homogénea cilíndrica que se mantiene horizontal. El modelo de simulación se construye en base a la ecuación de continuidad y la ley de Darcy, se usa como base lo expresado por Aziz y Settari (1979) y por Ertekin et al. (2001), se utiliza el método de solución simultánea (SS) y el método de Newton-Rhapson.
Es importante señalar que, a diferencia de la mayoría de simuladores comerciales, los cuales estiman la permeabilidad relativa del aceite en tres fases, a partir de los modelos de predicción, la herramienta desarrollada la estima de acuerdo a la función propuesta y los parámetros establecidos anteriormente. Las permeabilidades relativas del agua y del gas se obtienen directamente de las tablas dependientes de su propia saturación, de acuerdo a lo expresado por diversos autores (Oak, 1990) (Tarek, 2001) (Ertekin, et al., 2001). Para comprobar el correcto funcionamiento del simulador programado, se comparan los resultados obtenidos por éste, con los obtenidos por el simulador comercial IMEX-CMG y el simulador Sendra (especializado en la simulación de experimentos) para un par de casos genéricos. El primero consiste en una inyección de agua a tasa constante, en una roca tipo tapón que se encuentra inicialmente a saturación de agua irreducible, para este caso se comparan los resultados obtenidos entre Sendra y el simulador desarrollado.
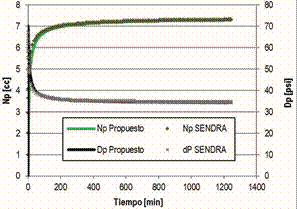
Figura 1. Comparación de resultados del simulador desarrollado con IMEX-CMG
para el caso trifásico
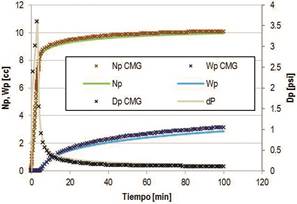
Figura 2. Comparación de resultados del simulador desarrollado con IMEX-CMG
para el caso trifásico
Note en la Figura 1, que se evidencia que existe un buen ajuste entre los resultados obtenidos con ambas herramientas, de manera que se puede afirmar que el simulador propuesto trabaja de manera correcta para el caso de dos fases.
Por otro lado, el segundo caso de comparación consiste en una inyección de 0.3 volúmenes porosos de agua, seguida de una inyección de gas a tasa constante, de manera que se presentará flujo de tres fases. La comparación se realiza para en esta ocasión con el software IMEX-GMG. La comparación del aceite y agua producidos, y del diferencial de presión obtenido por ambas herramientas se muestra en la Figura 2, Note que se obtiene un ajuste bueno para todas las variables, de manera que se puede afirmar que la función de simulación de flujo de tres fases funciona correctamente en la herramienta propuesta.
ALGORITMO DE AJUSTE AUTOMÁTICO
Para la estimación de los parámetros que permiten el ajuste entre lo experimental y lo simulado, y la consecuente estimación de las permeabilidades relativas, se propone un algoritmo de ajuste histórico automático, el cual consiste en dar solución a un problema de optimización numérica que busca minimizar la diferencia entre lo simulado y lo experimental, la cual se cuantifica por medio de la definición de una función objetivo, tal como se muestra en las expresiones (6) y (7).
Donde,
· Obj es la función a minimizar y que cuantifica numéricamente la diferencia entre lo experimental y lo simulado,
·
 es
el vector que contiene los parámetros de las funciones de permeabilidad
relativa,
es
el vector que contiene los parámetros de las funciones de permeabilidad
relativa,
· es el vector que contiene los datos medidos en el laboratorio experimentalmente (producción total de aceite, diferencial de presión, etc.),
· es el vector de datos simulados (dependiente de
· ),
·
 i es el subíndice que denota los
elementos de y , • n es el número total
de datos leídos,
i es el subíndice que denota los
elementos de y , • n es el número total
de datos leídos,
· j es el subíndice que denota el conjunto de datos se usa (ej. La producción acumulada de aceite y el de diferencial de presión son conjuntos de datos),
· k es el número de conjuntos de datos que se usan en el cálculo.
Para la minimización de la función objetivo seleccionada, se usa optimización numérica basada en el método de descenso optimal (Chapra y Canale, 2002), el cual consiste en suponer un valor inicial para los variables de diseño (los parámetros a optimizar) y encontrar la dirección en la cual la función presenta su mayor pendiente, y luego realizar una optimización unidimensional en esa dirección para estimar el desplazamiento que genera el mayor descenso, el proceso se repite hasta alcanzar un mínimo en la función. La Figura 3 muestra un esquema de cómo funciona este método para un caso de dos parámetros a estimar.
Figura 3. Esquema del método de máximo descenso
La dirección en la cual se debe mover la búsqueda para obtener el máximo descenso es contra-gradiente, por esto es necesario estimar el gradiente, lo que se hace numéricamente por medio de diferencias finitas centrales.
Una vez identificada esta dirección, se procede a determinar cuánto se debe avanzar para que se obtenga el máximo descenso, es decir, la magnitud del desplazamiento, la cual se nota como h, de esta manera el problema se convierte en una optimización unidimensional, donde la única variable de diseño a optimizar es h, para lo cual se recurre al método de sección aurea.
Es importante señalar los métodos de optimización de gradiente han sido usados eficazmente por diversos autores para estimar permeabilidades relativas (Fassihi, 1989) (Grattoni y Bidner, 1990) (Chavent, Jaffré y Jan, 1998) ( Nordtvedt, et al., 1997).
Los correspondientes algoritmos de optimización son implementados en Matlab y validados por medio de experimentos sintéticos realizados utilizando simulaciones, en las cuales los parámetros de las permeabilidades relativas son conocidos. Los resultados obtenidos muestran que los parámetros determinados coinciden con los usados en las simulaciones, por lo tanto, se puede inferir que, los métodos de optimización funcionan adecuadamente.
Como resultado se obtiene una herramienta que permite trabajar tres casos diferentes: 1) Inyección de agua en una roca saturada de aceite y agua irreducible. 2) Inyección de gas en una roca saturada de aceite y agua irreducible. 3) Inyección de gas en una roca saturada de agua y aceite móviles (caso tres fases).
Para los casos bifásicos, la herramienta permite optimizar cuatro parámetros: dos de curvatura (exponentes de Corey), la saturación residual de aceite y la permeabilidad relativa de la fase desplazante a dicha saturación. Para el caso de tres fases, además de los 8 parámetros de ambos casos de dos fases, se permite la optimización de los exponentes propuestos para modificar el modelo de Stone II (t1, t2) y la saturación irreducible de agua al gas (Swcg), para un total de once parámetros.
El programa desarrollado cuenta con una interfaz de usuario intuitiva y amigable, y diversas facilidades como la generación de diagramas ternarios. La Figura 4 muestra una captura de una de las ventanas de trabajo.
Figura 4. Captura de la interfaz de trabajo para el caso de tres fases
DESARROLLO EXPERIMENTAL
Con el fin de probar el desempeño del algoritmo desarrollado, se realizan dos conjuntos de experimentos, en cada conjunto se utilizan la misma roca y fluidos, para realizar tres desplazamientos diferentes, uno aguaaceite, uno gas-aceite (y agua irreducible) y uno de tres fases; se obtiene un total de seis experimentos.
Como diferencia principal entre el primer y el segundo conjunto de experimentos, se tiene que, en el desplazamiento de tres fases del primero, la inyección de gas para el experimento de tres fases, se inicia al alcanzar la saturación residual de aceite, mientras que, en el segundo conjunto, se inicia la inyección de gas después de inyectar 0.15 volúmenes porosos de agua, de manera que se obtiene un protocolo experimental similar al expuesto por Akhlaghina et al (2014).
Los desplazamientos del primer conjunto se realizan a tasas de 0.5cc/min para el desplazamiento con agua y de 1 cc/min para los desplazamientos con gas, mientras que, en el segundo conjunto se utilizan tasa de dos 2 cc/min para todos los desplazamientos. Las propiedades de las rocas utilizadas se muestran en la Tabla 1.
Tabla 1. Propiedades la roca utilizada en los experimentos
|
Propiedad |
Roca 1 |
Roca 2 |
|
Litología |
Arenisca |
Arenisca |
|
Longitud (cm) |
16.93 |
7.583 |
|
Diámetro (cm) |
3.812 |
3.7795 |
|
Permeabilidad al aire (mD) |
4.34 |
480 |
|
Porosidad por saturación (%) |
15.67 |
23.35 |
|
Volumen poroso (cc) |
30.28 |
19.86 |
APLICACIÓN DEL
ALGORITMO Y ESTIMACIÓN
DE PERMEABILIDADES RELATIVAS
La herramienta desarrollada se aplica sobre los experimentos realizados con el fin de determinar permeabilidades relativas de dos y tres fases. Los resultados obtenidos para dos fases se comparan con los obtenidos con el software Sendra, una herramienta diseñada para la estimación de permeabilidades relativas de dos fases, mediante el ajuste automático de la simulación de los experimentos.
La Figura 5 muestra los resultados del experimento de inyección de agua del primer conjunto (Exp 1), y el ajuste de la simulación obtenido con la herramienta desarrollada (estimado) y con Sendra. Similarmente, las curvas obtenidas en cada caso se muestran en la Figura 6.
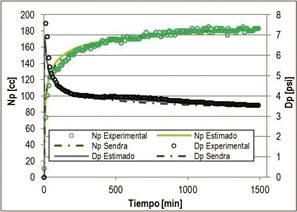
Figura 5. Comparación de ajuste con dos herramientas diferentes
para el Exp 1
herramientas diferentes para el experimento Exp 1
Observe que, las dos herramientas obtuvieron resultados prácticamente idénticos en este caso, lo que comprueba el correcto funcionamiento del algoritmo de estimación para el caso agua-aceite.
Un análisis similar al anterior se realiza con el desplazamiento gas-aceite del primer conjunto (Exp 2). El ajuste obtenido se muestra en la Figura 7, mientras que las curvas obtenidas se muestran en la Figura 8. Note que, nuevamente, los resultados obtenidos por ambos programas son muy similares, lo que confirma el buen funcionamiento del algoritmo propuesto, en casos gas-aceite. permeabilidades relativas de tres fases. Los resultados del ajuste obtenido se muestran en la Figura 9.
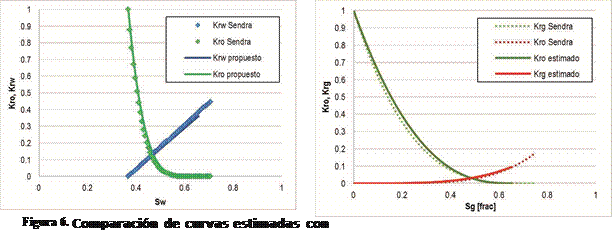
Figura 8. Comparación de curvas estimadas por medio de dos herramientas para el
experimento Exp 2
Por otro lado, se realiza la simulación de este experimento utilizando el enfoque clásico de yacimientos, en donde se asume que las permeabilidades relativas del agua y el gas son las mismas en dos y tres fases, y que las permeabilidades relativas del aceite en tres fases se pueden estimar por medio de un modelo de predicción a partir de las conocidas de dos fases (en este caso se usa el modelo de clásico de Stone II). La comparación de los resultados experimentales con los de la simulación cuando se usa el modelo clásico de Stone II, se muestra en la Figura 10.
después de la estimación de permeabilidades relativas
relativa agua-aceite estimadas para Exp 3, con las estimadas para Exp 1.
Figura 12. Comparación de curvas de permeabilidad relativa gas-aceite estimadas para Exp 3, con las estimadas para Exp
2 (Eje Y ampliado)
Observe que, existen cambios significativos entre las permeabilidades relativas estimadas para los experimentos de dos fases y las estimadas para el de tres fases, tanto para el agua y el gas, como para el aceite.
De acuerdo con lo anterior, se puede afirmar que, las permeabilidades relativas obtenidas con la metodología propuesta, permiten modelar el fenómeno del flujo en tres fases de una manera mucho más acertada que el enfoque clásico usado en yacimientos, principalmente, porque no se cumple la permeabilidad relativa del agua y el gas permanezca igual en tres fases que en dos fases; y adicionalmente, porque el modelo predictivo está lejos de poder describir las permeabilidades relativas del aceite en tres fases.
El mismo análisis realizado para los experimentos realizados con la primera roca, se repite con el segundo juego de experimentos, con el fin de reconfirmar los resultados obtenidos.
El ajuste mostrado para el experimento de inyección de agua (Exp 4), el cual se muestra en la Figura 15 y las curvas mostradas en la Figura 16, permiten reconfirmar que, la herramienta desarrollada tiene un desempeño similar a Sendra en los casos bifásicos.
Figura 15. Comparación de ajuste con dos herramientas diferentes para el experimento Exp 4
Figura 16. Comparación de curvas estimadas con dos herramientas diferentes para el experimento Exp 4
Por otro lado, el ajuste obtenido para el experimento Exp 6 (experimento de tres fases, Ver Figura 17), permite confirmar que el algoritmo propuesto es capaz de buscar las permeabilidades relativas tales que, se logra el ajuste entre lo experimental y lo simulado, mientras que los resultados expuestos en la Figura 18, donde se comparan los resultados de la simulación utilizando el modelo de Stone II, con los datos experimentales, evidencia que, aunque se reproducen de manera acertada, la producción de aceite y el diferencial de presión, nuevamente el recobro de agua fue sobrestimado.
Figura 17. Ajuste de la simulación del experimento Exp 6 después de la estimación de permeabilidades relativas
Figura 18. Ajuste de la simulación del experimento Exp 6 usando el modelo clásico de Stone II
Las permeabilidades relativas tres fases estimadas para la segunda roca, en comparación con las de dos fases, se muestran en la Figura 19 y la Figura 20. Note que, al igual que para la primera roca, la permeabilidad relativa del agua muestra una disminución, cuando se inicia el flujo de tres fases; es importante señalar que, en ambos experimentos de tres fases (Exp 3 y Exp 6), la saturación de agua primero aumenta durante la inyección de agua, para posteriormente disminuir con la inyección de gas, mientras que en los experimentos de inyección de agua (Exp 1 y Exp 4), la saturación de agua sólo incrementa, lo que indica que es posible que la fase salmuera esté exhibiendo un comportamiento asociado con fenómenos de histéresis, note que, la forma de las dos curvas encaja con la descripción de Killough (Killough, 1976) de la histéresis en permeabilidades relativas.
Figura 19. Comparación de curvas de permeabilidad relativa agua-aceite estimadas para Exp 6, con las estimadas para Exp 4 (Eje Y ampliado )
Figura 20. Comparación de curvas de permeabilidad relativa gas-aceite estimadas para Exp 6, con las estimadas para Exp
5 (Eje Y ampliado )
Por otro lado, para ambas rocas, la permeabilidad relativa del gas mostró un incremento en tres fases, con respecto a la estimada en dos fases, esto es un indicativo de que, en estos casos, la curva del gas tiende a presentar mayores valores, cuando la saturación de agua inicial al proceso de inyección de gas aumenta. Lo anterior es coherente con lo expresado por Pérez (2008) (Pérez, Santos y Zapata, 2008), quien afirma que para los experimentos de estado no-estacionario, la saturación inicial de las fases tiene efecto sobre las curvas estimadas.
Finalmente, las isopermas de permeabilidad relativa del aceite estimadas con el algoritmo propuesto y con el modelo de Stone II se muestran en la Figura 21 y la Figura 22, observe que, para ambas rocas, las superficies tienden a presentar mayor movilidad cuando la saturación de gas aumenta, y que las curvas son cóncavas hacia el vértice de la saturación de aceite, tal como las estimadas por Oak (1990), lo anterior es indicativo de que, para estos casos, la presencia de gas favorece la movilidad del crudo y la recuperación del mismo.
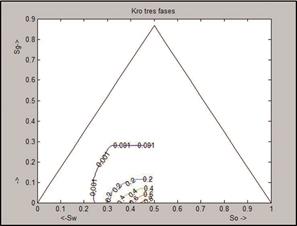
Figura 21. Líneas isopermas de permeabilidad de
aceite, estimadas para el Exp 3
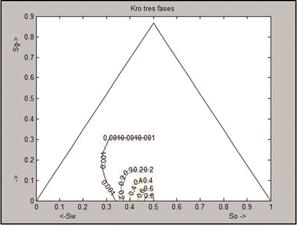
Figura 22. Curvas Isopermas de permeabilidad relativa
del aceite estimadas por medio del modelo de Stone II y de la información
de Exp 4 y Exp 5
CONCLUSIONES
Respecto a la metodología desarrollada en esta investigación, se encuentra que tanto el procedimiento de análisis, como el diseño de los montajes experimentales, fueron adecuados para la estimación de permeabilidades relativas de dos y tres fases, lo cual se pudo evidenciar en las simulaciones de los experimentos, las cuales reproducen correctamente los resultados observados en laboratorio, cuando se ingresan las curvas estimadas en cada caso, esto valida que las permeabilidades relativas estimadas, son adecuadas para describir el fenómeno observado. Como resultados se obtiene un código funcional en Matlab que realiza el ajuste automático de las simulaciones de los experimentos, determina permeabilidades relativas y genera diagramas ternarios de isopermas.
En lo relacionado con el enfoque clásico encontrado en la literatura para simular los desplazamientos de tres fases, en el cual, las curvas de agua y gas son las mismas para dos y tres fases, mientras que la permeabilidad del aceite se obtiene por un modelo de predictivo que usa la información de los sistemas agua-aceite y gas aceite (en esta investigación se usa Stone II), se encuentra que este tratamiento no es adecuado, ya que no permite en ninguno de los dos casos estudiados, reproducir el comportamiento de tres fases observado en el laboratorio. De manera general, el modelo de Stone II describió de forma aproximada el recobro de aceite, pero sobrestimo el recobro de agua.
Por otro lado, respecto a la predicción del diferencial de presión, el modelo de Stone II logra predecir correctamente el diferencial para el segundo conjunto de experimentos, pero falla considerablemente para el primer caso, esto confirma que este tipo de tratamiento al modelar el flujo de tres fases, no siempre funciona adecuadamente y en lo posible debe verificarse con ensayos como los planteados en este proyecto.
En lo referente a la comparación de las curvas estimadas para dos y tres fases, se encuentra que, hay cambios de unas respecto a las otras, por ejemplo, la curva de permeabilidad relativa encontrada para dos fases, en ambos conjuntos de experimentos, no permite reproducir el flujo observado en el caso de tres fases, sino que es necesario estimar una curva nueva. La comparación de estas curvas permite inferir que, el agua está siendo afectada por el fenómeno de histéresis, debido a que el cambio encontrado encaja con la descripción de Killough (1976), para un proceso de imbibición-drenaje, donde la permeabilidad relativa del agua se hace menor en el segundo ciclo (inyección de gas), cuando la dirección del proceso cambia y la saturación de ésta comienza a disminuir, lo que explica por qué, el modelo de Stone II sobre estima la producción de agua; también es posible que la disminución de la permeabilidad del agua se genere debido a la presencia de gas que dificulta su movimiento, sin estar directamente relacionada con la histéresis.
Finalmente, las curvas de gas estimadas permiten observar, en ambos casos, que la permeabilidad relativa de éste, tiende a ser mayor en tres fases, que en dos fases, de manera que incrementa cuando la saturación inicial de agua aumenta.
AGRADECIMIENTOS
Los autores quieren agradecer al Grupo de Investigación de Modelamiento de Hidrocarburos, a la Escuela de Ingeniería de Petróleos y al Laboratorio de Análisis Petrofísicos y Daño a la Formación de la Universidad Industrial de Santander (UIS), y al Laboratorio de Análisis Petrofísicos Especiales del Instituto Colombiano del Petróleo (ICP) y al Ingeniero Carlos Amaya por su constante apoyo a esta investigación.
REFERENCIAS