Revista
Fuentes: El Reventón Energético
Vol. 15 Nº 2 de 2017 - Jul/Dic - pp 71/78
PRESSURE AND PRESSURE
DERIVATIVE ANALYSIS FOR
ASYMMETRY FINITE-CONDUCTIVITY FRACTURED VERTICAL WELLS

Freddy Humberto Escobar1*; Cristhian
Eduardo Caicedo2; Alfredo Ghisays-Ruiz1
1Escuela de Ingeniería de Petróleos.
Universidad Surcolombiana (USCO). Avenida Pastrana-Cra 1. Huila, Colombia.
2 Escuela de
Física. Universidad del Atlántico. Km 7 antigua vía Puerto Colombia,
Barranquilla, Colombia.
*E-mail:
fescobar@usco.edu.co
ABSTRACT
Many researchers have
developed equations to characterize hydraulic fractures assuming they are
symmetrical with respect to the well, since symmetrical fractures are less
likely to occur. Therefore, since there is no direct analytical methodology
that allows an adequate interpretation using the pressure derivative function
to determine the fracture asymmetry, the position of the well with respect to
the fracture, fracture conductivity and half-fracture length. For this reason,
the TDS methodology that uses characteristic lines and points found in the
pressure and derivative log-log graphs is presented here to develop analytical
equations used to determine in a simple, practical and exact way the
aforementioned parameters. The technique was satisfactorily verified with synthetic problems.
Keywords: Fracture
Conductivity, Transient Pressure Analysis, TDS Technique, Fractured Wells.
ANALISIS
DE PRESIÓN Y DERIVADA DE PRESIÓN
PARA
POZOS FRACTURADOS ASIMÉTRICAMENTE CON FRACTURA DE CONDUCTIVIDAD FINITA
RESUMEN
Muchos investigadores han desarrollado ecuaciones para caracterizar
fracturas hidráulicas asumiendo que éstas son simétricas con respecto al pozo
puesto que las fracturas simétricas son menos probable que ocurran. Por lo
tanto, puesto que no existe una metodología analítica directa que permita una
adecuada interpretación utilizando la derivada de presión para determinar la
asimetría de la fractura, la posición del pozo con respecto a la fractura, la
conductividad de fractura y la longitud media de la misma. Por ello, aquí se
presenta la metodología TDS
que utiliza líneas y puntos característicos hallados en los gráficos loglog
de presión y derivada para desarrollar ecuaciones analíticas usadas para
determinar en forma simple, práctica y exacta los parámetros
anteriormente mencionados. La técnica se verificó satisfactoriamente con
problemas sintéticos.
Palabras clave: Conductividad
de fractura, análisis de pruebas de presión, Técnica TDS, Pozos fracturados.
Cita: Escobar, F.H., Caicedo,
C.E. y Ghisays-Ruz, A. (2017). Pressure
and pressure derivate analysis for asymmetry finiteconductivity fractured
vertical wells. Revista Fuentes:
El reventón energético, 15 (2), 71-78.
DOI: http://dx.doi.org/10.18273/revfue.v15n2-2017006
INTRODUCTION
The first fractured wells
began in 1860 and explosive materials such as nitroglycerin were used.
Subsequently began to use acids, leaving aside such materials, and finally in
1947 is studied the possibility of using water and only until 1952 in the
Soviet Union appears the first well fractured hydraulically. This technique
makes it possible to increase the hydrocarbon extraction from reservoirs with
low permeability, although lately it has been used in more permeable
formations, and has been so important that in year 2015, approximately, 60% of
the extraction wells in use used this technique.
Most of the published work
on the behavior of the pressure transient in fractured wells considers that the
fracture is symmetrical with respect to the axis of the well. However, it has
been shown that this may be the less likely case in reality, hence the
importance of studying the asymmetry of fractures in vertical wells and how this influences pressure
behavior.
Cinco–Ley, Samaniego and
Dominguez (1978) developed a mathematical model to study the behavior of the
pressure transient in a fractured vertical well with finite conductivity. Also
Narasimhan and Palen (1979) briefly discussed the influence of fracture
asymmetry on the behavior of well pressure under a constant rate of production.
Later, Bennet, Rosato, Reynolds and Raghavan (1983) studied this problem and
defined the conditions under which the asymmetry would have a negligible
influence on the well response. The problem was solved numerically in these
studies. However, no practical means have been provided for evaluating fracture
parameters, such as asymmetry, among others, since most of the solutions use
type-curve matching, Rodriguez, Cinco-Ley and Samaniego (1992) and Resurreicao
and Fernando (1991), which is a basically a trial-and-error procedure involving
uncertainty and tedious work.
Basically the purpose of
this work is to develop a practical interpretation technique for asymmetric
fractures observing and studying the behavior of pseudolinear and radial flow regimes by observations on the pressure and pressure
derivative plot. This methodology of
interpretation is an extension of the TDS (Tiab’s Direct Synthesis)
Technique, Tiab (1995). This
technique has been widely used for several cases of fractured wells. The most
important works on fractured wells using TDS technique were given by Tiab (1994)
and Tiab, Azzougen, Escobar and Berumen (1999). A recent work on pseudolinear
flow in fractured wells was
presented by Escobar, Gonzalez, Hernandez and Hernandez (2016). Escobar, Zhao and Zhang
(2014b) provided TDS Technique for
hydraulically-fractured wells in bi-zonal gas reservoirs. Escobar, Castro and Mosquera (2014c) provided a
rate-transient analysis methodology
for fractured wells. Escobar, Montenegro and Bernal (2014d) worked on shale reservoirs under transient-rate analysis and later
Bernal, Escobar & Ghisays-Ruiz
(2014a) extended this work to pressure transient analysis. Escobar, Ghisays-Ruiz and
Bonilla (2014d)
provided a new elliptical flow regime model for fractured wells. Zhao, Escobar, Hernandez
and Zhang (2016) developed an interpretation technique for fractured wells in
gas composite reservoirs and the works of Tiab and Bettam (2007) and Escobar,
Zhao and Fahes (2015) focus on fractured wells in naturallyfractured
formations.
MATHEMATICAL FORMULATION
Mathematical model
The mathematical model
proposed by Rodriguez, et al (1992) is given below :
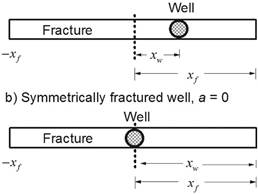
Figure 1. Schematic representation of fracture symmetry,
after
Rodriguez, et al. (1992).
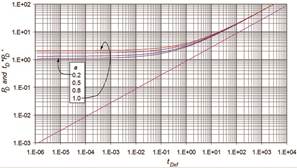
Figure 2. Dimensionless pressure and pressure derivative
behavior for a vertical fractured well with low fracture
conductivity, CfD = 1
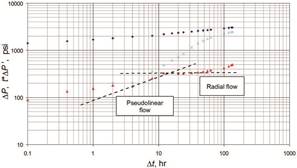
Figure 3. Pressure and pressure derivative against time
for an asymmetrically fractured well. Information from Bostic,
Agarwal and Carter (1980).
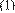
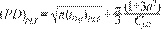
Which
pressure derivative was analytically taken:
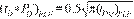
Suffix PLF stands for pseudolinear flow. The asymmetry factor “a” is a dimensionless parameter
defined as the ratio of
well position, xw, with the half-fracture length, xf. The asymmetry factor varies from
zero, in the case of a symmetrical fracture, to one, in the case of a well
located at the tip of the fracture. See Figure 1. The dimensionless pressure
and pressure derivative behavior obtained from Equations (1) and (2) are shown
in Figure 2. The impact of the asymmetry is observed there. As suggested by
equation (2), the asymmetry does not affect the pressure derivative curve;
then, a single curve is obtained for all cases. Such curve has a slope of ½ as
suggested by Equation (2). A typical case is presented by Bostic, et al (1980) in Figure 3 but because of
lacking of information
(gas gravity and wellbore radius) the problem was not solved here.
Dimensionless Parameters
The
dimensionless time, pressure and pressure derivative normally used in
transient-pressure analysis are given as:
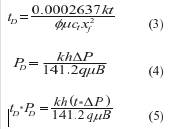
And the
dimensionless fracture conductivity, CincoLey, et
al (1978), is given by:
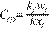

3. TDS TECHNIQUE FOR OIL
WELLS
Replacing
Equations (3) and (5) in Equation (2) and solving for the half-fracture length,
xf,
gives:
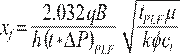
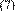
Division
of Equation (1) by (2) and replacement of Equations (3) to (5) on the resulting
expression leads to solve for the fracture asymmetry factor, a, so that:
Equation (8) includes a
correction factor introduced after the application of this equation.
Permeability and skin factors
can be estimated from, Tiab (1995);
Once
skin factor and the half-fractured length are known, the fractured conductivity
can be estimated from a correlation presented by Tiab (2003).
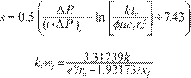

4. TDS TECHNIQUE FOR GAS
WELLS
The
dimensionless time for gas with rigorous time and pseudotime,
Agarwal (1979), are:
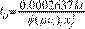
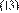
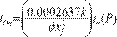
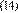
And the
pseudopressure and pseudopressure derivative are given by:
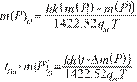

With
these dimensionless quantities Equations (7) and (8) become:

The
permeability and skin factor are found from, Nunez, Tiab and Escobar (2003) and
Escobar, Lopez and Cantillo (2007):
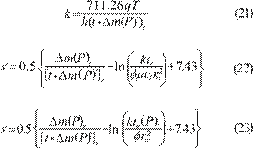
SYNTHETIC
EXAMPLES
Oil Example
A pressure test was
simulated for an oil reservoir with a hydraulically-fractured vertical well having finite conductivity. The input data is
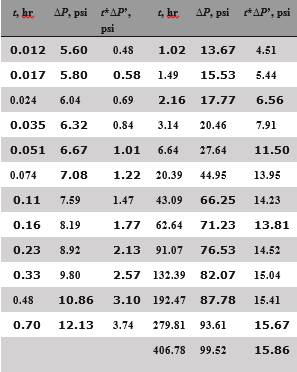
given in Table 1 and simulated results are presented in Table 2 and Figure 4. It is requested to estimate
permeability, asymmetry, half-fracture
length and fracture conductivity.
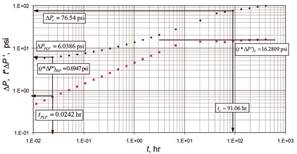
Figure 4. Pressure and pressure derivative against time
loglog plot for oil example.
Table 1. Well, reservoir and fluid data for the worked
examples.
|
Parameter
|
Oil Example
|
Gas Example
|
|
q
|
430 BPD
|
500 Mscf/D
|
|
B
|
1.12 bbl/STB
|
0.0107 bbl/SCF
|
|
µ (cp)
|
2.3
|
0.0107
|
|
h (ft)
|
80
|
50
|
|
xw (ft)
|
120
|
90
|
|
xf (ft)
|
400
|
500
|
|
|
0.18
|
0.07
|
|
ct (1/psi)
|
1x10-5
|
2x10-6
|
|
k (md)
|
60
|
0.01
|
|
T, °R
|
|
720
|
|
CfD
|
8
|
10
|
Table 2. Pressure and pressure derivative data for oil
example.
Estimate
fracture conductivity with Equation (6):
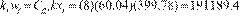
Finally,
find asymmetry with Equation (8):
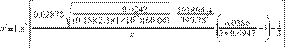
a = 0.3
The estimation of xf, a, and xw has an error of 0.06 %, 0 % and
0.08 %, respectively, with respect to the input data used to run the
simulation.
Gas Example
A pseudopressure test was
simulated for a gas reservoir drained by a
hydraulically-fractured finite-conductivity vertical well. The input data is given in Table
1 and simulated results are presented in Table 3 and Figure 5. Find
permeability, asymmetry, half-fracture length and fracture conductivity for
this test.
Solution. The following data were read from
Figure 5.
[t*∆m(Pꞌ)]r = 512114869 psi2/cp tPLF = 0.04107 hr
[t*∆m(Pꞌ)]PLF = 15020549.4 psi2/cp
[∆m(P)]PLF = 1.41x108 psi2/cp Find permeability with Equation (21):
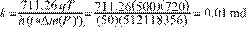
Find the half-fracture
length with Equation (17):
for gas example.
|
t,
hr
|
∆m(P), psi2/cp
|
t*∆m(P’),
psi2/cp
|
t,
hr
|
∆m(P), psi2/cp
|
t*∆m(P’),
psi2 /cp
|
|
0.028
|
1.36E+08
|
12457641.2
|
5.32
|
4.53E+08
|
170976262
|
|
0.041
|
1.41E+08
|
15020549.4
|
7.74
|
5.23E+08
|
206151177
|
|
0.060
|
1.47E+08
|
18110724.3
|
11.25
|
6.08E+08
|
248562620
|
|
0.087
|
1.54E+08
|
21836640.2
|
16.35
|
7.10E+08
|
299699362
|
|
0.126
|
1.63E+08
|
26329088.1
|
23.77
|
8.33E+08
|
361356456
|
|
0.183
|
1.74E+08
|
31745766.5
|
34.56
|
9.82E+08
|
435698253
|
|
0.267
|
1.87E+08
|
38276817.2
|
50.24
|
1.16E+09
|
422912933
|
|
0.388
|
2.03E+08
|
46151499.7
|
73.04
|
1.38E+09
|
428568437
|
|
0.564
|
2.22E+08
|
55646239.2
|
106.18
|
1.64E+09
|
456458589
|
|
0.819
|
2.45E+08
|
67094329.7
|
154.36
|
2.18E+09
|
413422131
|
|
1.19
|
2.73E+08
|
80897633.7
|
224.41
|
2.34E+09
|
434154181
|
|
1.73
|
3.06E+08
|
97540688.8
|
326.24
|
2.51E+09
|
456556408
|
|
2.52
|
3.46E+08
|
117607717
|
474.28
|
2.68E+09
|
472665728
|
|
3.66
|
3.94E+08
|
141803130
|
689.50
|
2.86E+09
|
484225857
|
Find fracture conductivity
with Equation (6)
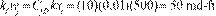
Determine the asymmetry with Equation (19):
a = 0.19
The estimation of xf, a, and xw has an error of 0 %, 5.3 % and 5.3
%, respectively, with respect to the input data used to run the simulation.
ANALYSIS
OF RESULTS
All the obtained results
match quite well with the input values used for running the simulations. In the
gas example the asymmetry factor value was 0.18 compared with 0.19 from the computations. Although, the difference looks so small, the
absolute error is 5.3 % which stills is valid in pressure transient analysis.
Notice that with actual data probably the fracture conductivity is unknown. If
so, it can be estimated with Equation (12). The oil example provided better
results compared to the gas example which may be due to the fact that the gas uses the pseudopressure function
which is an artificial function that may cause the error to be slightly
higher.
CONCLUSION
Equations for vertical
wells in oil and gas reservoirs were developed following the philosophy of the TDS Technique to characterize such
asymmetrically fractured wells parameters
as half-fracture length, well position and asymmetry factor. The
deviation error obtained from the exercise is very low.
REFERENCES
Agarwal, R. G. (1979).
“Real Gas Pseudo-Time” - A New Function For Pressure Buildup Analysis Of MHF
Gas Wells. Society of Petroleum
Engineers. doi:10.2118/8279-MS.
Bennett, C. O., Rosato, N.
D., Reynolds, A. C., & Raghavan, R. (1983). Influence of Fracture Heterogeneity
and Wing Length on the Response of Vertically Fractured Wells. Society of Petroleum Engineers, 23 (02).
doi:10.2118/9886-PA.
Bernal, K.M., Escobar,
F.H., & Ghisays-Ruiz, A. (2014a). Pressure and Pressure Derivative Analysis
for Hydraulically-Fractured Shale Formations Using the Concept of Induced
Permeability Field. Journal of
Engineering and Applied Sciences, Vol. 9 (10), 1952-1958. ISSN 1819-6608.
Cinco-Ley, H., Samaniego V., F., & Dominguez, A., N. (1978, August 1). Transient Pressure Behavior for a
Well With a Finite-Conductivity Vertical Fracture. SPE
Journal. 18(4), 253264. doi:10.2118/6014-PA.
Bostic, J. N., Agarwal, R.
G., & Carter, R. D. (1980). Combined Analysis of Postfracturing
Performance and Pressure
Buildup Data for Evaluating an MHF Gas Well. Society of Petroleum Engineers, 32 (10). doi:10.2118/8280-PA.
Escobar, F.H., Lopez, A.M.
& Cantillo, J.H. (2007). Effect of the Pseudotime Function on Gas Reservoir
Drainage Area Determination. CT&F – Ciencia, Tecnología y Futuro, 3 (3), 113-124. ISSN 0122-5383.
Escobar, F.H., Zhao, Y.L., & Zhang, L.H. (2014b). Interpretation of Pressure Tests in Hydraulically-Fractured
Wells in Bi-Zonal Gas Reservoirs. Ingeniería e Investigación Journal, 34 (4), 76-84. ISSN 0120-5609.
Escobar, F.H., Castro, J.R. & Mosquera, J.S. (2014c). Rate-Transient Analysis for Hydraulically
Fractured Vertical Oil and Gas Wells. Journal of Engineering and Applied Sciences,
9 (5), 739-749 . ISSN 1819-6608.
Escobar, F.H., Montenegro,
L.M. & Bernal, K.M. (2014d). Transient-Rate
Analysis For Hydraulically-Fractured Gas
Shale Wells Using The Concept Of Induced
Permeability Field”. Journal of
Engineering and Applied Sciences, 9 (8), 1244-1254. ISSN 1819-6608.
Escobar, F.H., Ghisays-Ruiz, A. & Bonilla, L.F. (2014e). New Model for Elliptical Flow Regime
in Hydraulically-Fractured Vertical
Wells in Homogeneous and
NaturallyFractured Systems. Journal of
Engineering and Applied Sciences, 9 (9), 1629-1636. ISSN 1819-6608.
Escobar, F.H., Zhao, Y.L. & Fahes, M. (2015). Characterization of the naturally fractured reservoir
parameters in infinite-conductivity hydraulically-fractured vertical wells by
transient pressure analysis. Journal
of Engineering and Applied Sciences, 10 (12), 5352-5362.
Escobar, F.H., Gonzalez, R.A., Hernandez, L.M. & Hernandez, C.M.
(2016). Pressure and Pressure
Derivative Analysis for Hydraulically Fractured Vertical Wells with Face Skin. Journal of Engineering and Applied Sciences,
11 (13), 8268-8273.
Narasimhan, T. N., & Palen, W. A. (1979). A Purely Numerical Approach For Analyzing Fluid
Flow To A Well Intercepting A Vertical Fracture. Society of Petroleum Engineers.
doi:10.2118/7983-MS.
Nunez, W., Tiab, D., & Escobar, F. H. (2003). Transient Pressure Analysis for a Vertical Gas
Well Intersected by a Finite-Conductivity Fracture. Society of Petroleum
Engineers.
doi:10.2118/80915-MS.
Resurreicao, C. E. S., & Fernando, R. (1991). Transient Rate Behavior of Finite-Conductivity
Asymmetrically Fractured Wells Producing at Constant Pressure. Society of Petroleum Engineers. doi:10.2118/22657-MS
Rodriguez, F., Cinco-Ley, H., & Samaniego-V., F. (1992). Evaluation of Fracture Asymmetry of
Finite-Conductivity Fractured Wells. Society
of Petroleum Engineers, 7 (02). doi:10.2118/20583-PA.
Tiab, D. (1994). Analysis
of Pressure Derivative without Type-Curve Matching: Vertically Fractured Wells
in Closed Systems. Journal of Petroleum Science and Engineering 11 (1994) 323-333.
This paper was originally presented as Tiab, D. (1993, January 1). Analysis of Pressure
and Pressure Derivative without TypeCurve Matching - III. Vertically Fractured
Wells in Closed Systems. Society of
Petroleum Engineers. doi:10.2118/26138-MS
Tiab, D. (1995). Analysis
of Pressure and Pressure Derivative without Type-Curve Matching:
I-Skin and Wellbore
Storage. Journal of Petroleum Science and Engineering, Vol. 12, pp.
171-181.Also Tiab, D. (1993, January 1). Analysis of Pressure and Pressure
Derivatives Without Type-Curve Matching: I-Skin and Wellbore Storage. Society of Petroleum Engineers. doi:
10.2118/25426-MS.
Tiab, D., Azzougen, A.,
Escobar, F. H., & Berumen, S. (1999, January 1). Analysis of Pressure Derivative
Data of
Finite-Conductivity Fractures by the
“Direct Synthesis” Technique. Society of Petroleum Engineers. doi:10.2118/52201-MS.
Tiab, D. (2003). Advances
in pressure transient analysis — TDS technique. Lecture Notes Manual. The University of Oklahoma, Norman, Oklahoma,
USA. 577p.
Tiab, D., & Bettam, Y.
(2007). Practical Interpretation of Pressure Tests of
Hydraulically Fractured
Wells in a Naturally Fractured Reservoir. Society of Petroleum Engineers. doi:10.2118/107013-MS.
Zhao, Y.L. Escobar, F.H., Hernandez, C.M., & Zhang, C.P. (2016).
Performance Analysis of a Vertical
Well with a
Finite-Conductivity Fracture in Gas Composite Reservoirs. ARPN Journal of Engineering and Applied
Science1819-6608, 11 (15), 8992-9003.
NOMENCLATURE
a
|
Asymmetry factor
|
B
|
Volume factor, for oil
the units are bbl/STB, for gas the units are bbl/SCF
|
ct
|
Total compressibility, 1/psi
|
CfD
|
Dimensionless fracture conductivity
|
h
|
Formation thickness, ft
|
k
|
Permeability, md
|
kfwf
|
Fracture conductivity, md-ft
|
q
|
Oil flow rate, BPD
|
qsc
|
Gas flow rate, Mscf/D
|
rw
|
Well radius, ft
|
PD
|
Dimensionless pressure
|
t
|
Time, hr
|
tD
|
Dimensionless time base
on well radius
|
tDA
|
Dimensionless time base
on area
|
tD*PD’
|
Dimensionless pressure derivative
|
t*∆P’
|
Pressure derivative, psi
|
∆P
|
Pressure change, psi
|
xf
|
Half-fracture length, ft
|
xw
|
Well position along the
fracture, ft
|
Suffixes
D Dimensionless
Dxf Dimensionless based on half-fracture length PLF Pseudolinear
r Radial w Well
![]()