1. INTRODUCCIÓN
El diseño y construcción de puentes ha ido
evolucionando exponencialmente hasta la actualidad. A pesar de que son los
parámetros subyacentes al proyecto de obra [1] [2] [3] [4] [5] [6] los que
definen la metodología estructural a utilizar, aún se observa que es posible la
elección entre varias tipologías estructurales y diseños para un mismo caso.
Entre ellas se encuentra la construcción por voladizos sucesivos in situ,
siendo esta la metodología abarcada en el presente estudio. Este método
constructivo se define como [7] la ejecución del tablero del puente avanzando
por tramos sucesivos, haciendo soportar a la parte ya construida el peso del
tramo en construcción. Cada tramo o dovela se une y funde al precedente cuando
adquiere una resistencia suficiente. Entonces se convierte en autoportante y
sirve de base de arranque para un nuevo tramo. El primero que utilizó esta
forma de diseño y construcción fue Freyssinet en 1928; sin embargo, fue
Baumgart en 1930 quien diseñó y construyó de esta manera el puente Herval en
Brasil. En Colombia [2] el primer uso de esta tipología se da en el puente
Currulao en Urabá (1962). En la figura 1 se muestran fotos del momento de su
ejecución.

Figura 1. Ejecución del puente Currulao
en Uraba (1962).
Fuente. Ingeniero. Mario Rodriguez –
Precomprimidos S.A.
En el cálculo y diseño estructural de un
puente, el proceso constructivo es algo inherente al modelo analítico, no puede
estudiarse y tratarse uno de ellos sin considerar el otro. En el método de
voladizos sucesivos no hay muchas posibilidades de variación de método en el
proceso constructivo, pero no ocurre así en el diseño; donde se han dado
variaciones significativas a lo largo de los años. Es por ello que en este
estudio se comparan las distintas teorías de predimensionamiento utilizadas en
las últimas décadas para entender la evolución de los puentes diseñados hasta
hoy. También se trata la variación del proceso constructivo en la historia;
que, aunque como se ha dicho es escasa, debe mencionarse.
2. TEORÍAS DE PREDIMENSIONAMIENTO
Se presentan 5 teorías [8][9][3] [10]11]
sobre el predimensionamiento, de las que se van a exponer tanto sus semejanzas
como sus diferencias. Mayoritariamente se centran en la sección transversal,
pero también dan consejos para la sección longitudinal del puente. Estas
teorías van desde el 1978 hasta la fecha.
En las figuras 2 y 3 se muestran los
parámetros geométricos que se van a tratar en el estudio de las distintas
teorías.
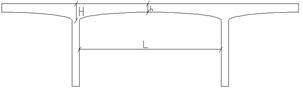
Figura 2. Vista de la sección
longitudinal de un puente típico donde se muestran las variables estudiadas.
Fuente.
Elaboración propia.
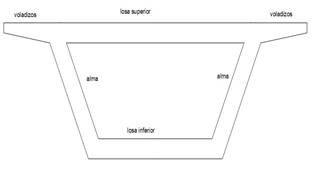
Figura 3. Vista de la sección
transversal donde se muestran las variables estudiadas. Fuente. Elaboración
propia.
2.1 Precast segmental box girder manual
(1978)
Este documento elaborado por los institutos
de pretensado y postensado de EE.UU (PTI y PCI) establece valores basados en
la experiencia, pero da información limitada y generalizada. Los valores que recoge
son relaciones y aproximaciones entre los parámetros mostrados en la figura 2 y
la figura 3. Estos valores se muestran a continuación:
•
Relación H/L: 1/18 – 1/20
•
Relación h/L: 1/40 – 1/50 • Voladizos: ¼ del
ancho del tablero.
•
Espesor losa superior:17.5cm-25cm
•
Alma: 25cm mínimo, recomendable 35cm
•
Espesor losa inferior: Mínimo 17.8cm
2.2 Construcción de puentes de hormigón pretensado
por voladizos sucesivos. Mathivat. (1980)
Esta teoría de predimensionamiento fue
desarrollada por J. Mathivat (1980) y trata sobre la experiencia del autor.
Establece algunas teorías elementales.
Entre ellas que es mejor pocas almas y
anchas, que muchas y estrechas, ya que así se ahorra material; o la validez de
cajones monocelulares para anchuras de tablero de hasta 12m. Se habla sobre
cizalladura y sobre el acero de refuerzo.
2.3 Setra (2003)
Fue desarrollado por un conjunto de
ingenieros franceses y resume la historia de este tipo de puentes tanto en
Francia como en el resto del mundo y además da directrices concretas sobre el
diseño de estos. Particularmente trata cada elemento por separado (losa
superior, losa inferior, almas, etc.) con sus respectivas recomendaciones para
su diseño particular.
Aporta a todo lo tratado en las anteriores
teorías el concepto de losa superior postensada, diseño del alma inclinada y
comportamiento del postensado en el proceso constructivo.
2.4 Puentes. Apuntes para su diseño, cálculo y
construcción. Manterola (2006)
Fue escrito por un ingeniero español [12]
con más de 200 diseños de puentes. Ofrece teorías basadas en su experiencia.
Corrobora algunas de las teorías
anteriores, como la de Mathivat. Contempla la opción de variar el espesor de la
losa inferior; descendiendo este conforme se aleja de los pilares.
2.5 Criterios para la optimización del predimensionamiento
de puentes en sección cajón.
Ariñez (2012)
Es de los estudios más actualizados [11] de
predimensionamiento de puentes de la tipología estudiada. Abarcan toda la
información hasta el momento (incluyendo diferentes normas) y la procesan
resultando, que las almas inclinadas son más eficientes que las rectas en
cantos pequeños, y al contrario en las grandes.
Se hace un aporte muy importante, y es que
establece que la relación óptima entre la luz (L) y el canto sobre pilares (H)
es 1/17, y que es mejor respetar este límite que aumentar espesores de los
elementos.
2.6 Comparativa de teorías de predimensionamiento
Se procede a comparar las distintas teorías
de predimensionamiento para unos mismos valores iniciales, que son los
siguientes:
•
Luz longitudinal (L)=100m
•
Ancho de tablero=12m
•
L/H=1/20
•
L/h=1/50
Operando según las distintas teorías
de predimiensionamiento, se obtienen valores de:
•
Espesor losa superior
•
Espesor losa inferior
•
Ancho de alma
•
Separación entre almas (S)
•
Espesor de voladizos
Además, se obtiene el área transversal
asociada a los puntos donde se define H y h, la relación entre ellas, y el
promedio de todas las teorías. También se analiza la relación entre estos
resultados. Estos resultados se muestran en la tabla 1.
Tabla 1 Resumen de comparativa
de teorías de predimensionamiento.
|
cm
|
Precast (1978)
|
Mathivat (1980)
|
SETRA
(2003)
|
Manterola (2006)
|
Ariñez (2012)
|
|
|
Losa sup
|
24
|
22
|
24
|
28
|
30
|
|
Losa inf
|
20
|
20
|
20
|
22
|
22
|
|
Almas
|
30
|
27
|
26
|
28
|
27
|
|
S
|
600
|
600
|
600
|
720
|
720
|
|
Voladizos
|
-
|
-
|
80
|
65
|
48
|
Promedio
|
|
AREA en H (m2)
|
5.45
|
5.08
|
5.79
|
6.82
|
7.03
|
6.034824
|
|
AREA en h (m2)
|
4.61
|
4.32
|
4.99
|
5.96
|
6.20
|
5.216664
|
|
Relación
|
1.18
|
1.17
|
1.16
|
1.14
|
1.13
|
|
Fuente. Elaboración propia.
Se aprecia que, con el paso del tiempo, se
ha tendido a aumentar el espesor de la losa superior, así como de la inferior.
Esto es debido a la importancia del concepto de losa de compresión. A la par
que se ha aumentado la separación S entre almas, se recortado el largo de los
voladizos, por lo que su espesor disminuye.
Además, debe mencionarse la tendencia de
las teorías más novedosas a arrojar resultados de área transversal en H y h más
altos que las teorías predecesoras, mientras que la relación entre ambas va
disminuyendo. Una de las causas de esta evolución es el constante desarrollo de
las normativas y acciones de diseño. Esto significa que, como se verá más
adelante; se tiende a que la curvatura de la sección longitudinal no sea hoy en
día tan pronunciada como lo era en los diseños antiguos.
3. PROCESO CONSTRUCTIVO
Los puentes en voladizos sucesivos se
construyen por etapas [2] [4] [13] [14] [15] [16]. Cada etapa corresponde a la
construcción de cada una de las dovelas que forman el puente, como se
representa esquemáticamente en la figura 4. Este proceso de construcción se
puede dividir en tres partes, según su orden de ejecución. Estas son
Operaciones Preliminares (Dovela de pila), Operaciones Básicas (Ejecución de
voladizos sucesivos) y
Operaciones Posteriores (Dovela de cierre).
La construcción por avance en voladizo
consiste en la ejecución de las dovelas (entre 3 y 5 metros de longitud) a
ambos lados de la pila, de forma simétrica. El vaciado se realiza con la ayuda
de los encofrados, que a su vez se apoyan en las dovelas anteriores mediante
cimbras para garantizar la continuidad del puente, por medio de cables de
postensado. Vaciando las dovelas sucesivamente sobre los carros, se va
avanzando desde las pilas hasta el centro del vano conectando mediante la
dovela clave con el último voladizo del grupo perteneciente a la pila contigua.
El inicio de todo el proceso se da con la
construcción de la dovela situada encima de la pila o también denominada dovela
“0” o dovela de pila. Esta dovela se construye con un encofrado montado sobre
la pila con longitud suficiente para que se puedan montar los carros de avance.
Esto se aprecia en la figura 5.
3.1 Operaciones Preliminares (Dovela de Pila)
Se vacía la dovela de la pila o dovela “0”.
Inicialmente se construye la losa inferior de la sección, montando su
formaleta, seguido del encofrado del alma y terminando con el acero de refuerzo
y vaciado de la losa superior. Finalmente se retira toda la formaleta. Se puede
concebir tanto quedando esta dovela empotrada en la pila, como simplemente
apoyada sobre ella.
Figura 5.
Vista de la ejecución de la dovela 0 en el viaducto de
Tenoya, en Tenerife (España).
Fuente.
https://elblogingenierocivil.wordpress.com/
3.2 Operaciones Básicas de Ciclo (Ejecución de
voladizos sucesivos)
3.2.1 Carro de avance.
El carro de avance es el medio más común
que se tiene para la construcción del puente por voladizos sucesivos. Sirve
para trasladar los encofrados y fundir las dovelas. Es la zona de trabajo de
los operarios. Se muestra en las figuras 6, 7 y 8.
El carro está formado por las vigas
metálicas principales, las vigas transversales, las vigas de rodadura, los
apoyos frontales y traseros, los pisos de trabajo y los elementos y plataformas
auxiliares.
Tras el montaje de la dovela de pila, se
incorpora a ella el primer carro para la construcción de la dovela 1. Una vez
finalizada el carro se desplaza para la construcción en voladizo de las dovelas
sucesivas de dicho tramo. Así se libera la cabeza de pila para que pueda
recibir al segundo carro que se ocupará de la construcción del tramo simétrico.
Una vez montado el carro de avance, se
hacen revisiones periódicas tanto en el avance del carro, como en el vaciado;
ya que en estos momentos son donde se dan las solicitaciones más críticas.
de-avance/
3.2.2 Ejecución de dovelas.
A continuación, se describen las
operaciones para ejecutar una dovela con vaciado in situ.
•
Avance y fijación del carro. Es el primer paso.
Comienza cuando el hormigón alcanza la resistencia necesaria para ser tensado y
puede soportar el carro de avance.
•
Colocación del acero de refuerzo inferior. Se
monta manualmente el acero de refuerzo de la losa inferior.
•
Formaleta. Se formaletea el resto de la sección.
•
Colocación del acero de refuerzo superior. Se
monta el acero de refuerzo de la losa superior y las vainas de los cables.
•
Nivelación del carro. Paso previo al vaciado.
•
Vaciado de la dovela. Durante el proceso, el
carro se sujeta en los gatos y se ancla al tablero. A medida que se va
reduciendo el canto, se deben desmontar los paneles sobrantes. Primero se
hormigona la losa inferior y se va ascendiendo para terminar con la losa
superior.
•
Desmontaje de la formaleta de las dovelas.
•
Curado del concreto. Debe evitarse la aparición
de fisuras.
•
Enfilado y tensado de los cables.
•
Inyección de las vainas.
3.3 Operaciones Posteriores (Dovela de cierre)
Finalizado el vaciado de las dos últimas
dovelas y antes de ejecutar la dovela de cierre, se procede a desmontar el
carro de avance.
A continuación, se vacía la dovela de
cierre, que es la encargada de unir los dos tramos que se han ido construyendo
por voladizos sucesivos. Este momento es importante porque se transforman dos
voladizos independientes entre sí en un vano que trabaja como una viga sustentada
en dos apoyos. Para ejecutar la dovela de cierre, se inmovilizan, con vigas
metálicas; los dos semivanos. Estos semivanos son independientes entre sí
porque provienen de distintas pilas. Así se puede utilizar la plataforma
inferior de uno de los carros como superficie de trabajo. Se utilizan
formaletas distintas a las anteriores; ya que estas son mucho más ligeras.
Finalmente, se realiza el tensado de
continuidad, produciéndose así la unión de los dos voladizos y convirtiéndolos
en una viga continúa preparada para absorber las cargas móviles estipuladas.
Dentro de la zona hueca del tablero se introducen los equipos de enhebrado de
cables de postensado. Después éstos se enfilan para posteriormente tensarlos y
darle continuidad a la estructura. Para introducir los cables se utilizan los
ductos que se han dejado en la losa superior para dicho propósito. Las vainas
de los cables de continuidad se inyectan también desde la losa superior del
tablero.
Finalmente se deben tapar los agujeros que
se dejan para el anclaje del carro de avance, así como la instalación de juntas
de dilatación si están proyectadas sobre el tablero.
3.4 Variante de construcción por voladizos sucesivos
Figura 9. Construcción por voladizos
sucesivos desde los estribos. Fuente. SETRA.
Hasta ahora sólo se ha contemplado la
construcción desde los pilares, pero hay una variante de esto. Cuando se debe
salvar un vano pequeño, que no requiere pilares; se construye desde los
estribos para unirse en el centro del vano como se muestra en la figura 9.
Para ello se colocan contrapesos en los
estribos que soportan el peso de lo que se está construyendo hasta ahora como
se muestra en la figura 10.
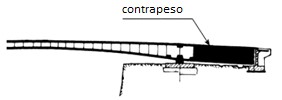
Figura 10. Vista de perfil de los
contrapesos que sujetan los voladizos. Fuente. SETRA.
3.5 Variación de momentos durante la construcción
Una de las características de este tipo de
construcción es que, durante su construcción, la estructura sufre diversas
solicitaciones que pueden llegar a contrarrestarse con el paso del tiempo.
3.5.1 Tensiones iniciales.
3.5.2 Tensiones al unirse al estribo.
Cuando toman continuidad uniéndose al
estribo aparecen los momentos positivos en la estructura como se muestra en la
figura 12.
Al darle continuidad a la totalidad de la
estructura se observa que el valor de los momentos negativos disminuye, los
momentos positivos aumentan y además aparecen éstos en la unión de los
voladizos como se muestra en la figura 12.

Figura 13. Momentos en la fase de unión
a los voladizos sucesivos. Fuente. Elaboración propia.
3.6 Evolución del proceso de diseño y constructivo
Desde los primeros cálculos y
construcciones de este tipo de puentes hasta hoy en día se han dado varios
tipos de culminación de obra [3]. Se muestran a continuación por orden
cronológico.
3.6.1 Puentes de primera generación. Este periodo abarca los años entre 1953 y 1964. Los tableros de este
tipo de puentes llamados de primera generación se construían unidos
monolíticamente tanto a los pilares como a los estribos. Además, los voladizos
entre ellos no se unían dándole continuidad, sino que se utilizaban las uniones
machihembradas.
En 1957 se construyó el puente Casey y el
puente Beaucaire con esta unión machihembrada. Este tipo de puentes han tenido
muchos problemas de deflexiones a lo largo de la historia; y por esta razón
estos dos puentes fueron demolidos en 1973 y 1995 respectivamente. A raíz de
estas experiencias han aparecido los denominados puentes de segunda generación.
3.6.2 Puentes de
segunda generación. Como los puentes de primera
generación sufrieron una deformación excesiva de sus elementos en voladizo con
el paso del tiempo, debido a una subestimación de los efectos de la fluencia
lenta del hormigón y la contracción, se evolucionó a lo que se denomina segunda
generación de puentes, que abarca desde el año 1965 al 1975. La diferencia
fundamental entre los puentes de ésta generación y de la primera es que se
contempla una estructura continua y monolítica; es decir, sin la unión machiembrada
entre los voladizos en mitad del tramo. Se muestra la diferencia en las figuras
14 y 15.
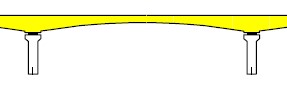
Figura 15. Detalle típico de la
continuidad de la estructura de los puentes de segunda generación. Fuente.
SETRA.
Este fue un período de enormes desarrollos
y regulaciones que cambiaban constantemente en base a la experiencia del
momento. También se aprecia como estos puentes de segunda generación aún
tuvieron que repararse y repotenciarse con el paso de los años. Todos los
progresos que se dieron allanaron el camino a la llamada tercera generación.
3.6.3 Puentes de tercera generación. Se denomina así a los puentes diseñados y construidos entre 1975 y
1982. La diferencia con las generaciones anteriores es que estos puentes ya
cuentan en el cálculo con la fluencia y el gradiente térmico, siendo estos
factores muy importantes en la vida útil de la estructura.
Por tanto, se consideran estructuras mejor
diseñadas que las anteriores y hoy en día no sufren los problemas que han
sufrido los puentes de otras generaciones.
Se aprecia que ya en esta generación se
tratan nuevas tecnologías de diseño como variar el tipo de hormigón o construir
luces no balanceadas.
3.6.4 Época actual.
En esta época ya se generalizan los
reglamentos de los cálculos estructurales; y además se introduce el concepto de
control de calidad. Por otra parte, se desarrolla el pretensado exterior.
4. SELECCIÓN DE PUENTES A ESTUDIAR
Se tiene datos de 124 puentes [17] [18]
[19] construidos en voladizos sucesivos in situ. Para considerar un puente como
válido en este estudio se ha debido obtener mínimo el valor de la luz principal
(L), el país al que pertenece y su fecha de diseño. Este grupo de datos se ha
clasificado a su vez siguiendo tres criterios:
•
Cronología
•
Luz libre
•
Países
A su vez, se ha estudiado según los
criterios anteriores; la relación entre la luz principal y el canto en apoyos y
el canto en el centro (L/H y L/h) así como la relación entre los dos cantos
(h/H).
Además, dentro de esos tres criterios la se
ha medido relación entre su luz principal (L) y las relaciones anteriores (L/H,
L/h y h/H). Estos resultados se comparan con los clásicos L/50 y L/20.
Seguidamente se presentan gráficas paramétricas donde se aprecian los campos de
aplicación de esta tipología.
4.1 Cronología
Se presentan los datos clasificados en
orden cronológico.
Esto es, se dividen los datos en tres
grupos. Estos son:
•
1960-1980 • 1980-2000
•
2000-2016
4.1.1 1960-1980.
Se tienen datos geométricos de 50 puentes
diseñados y construidos durante estos años, pertenecientes a 13 países (España,
Colombia, Francia, Alemania, Noruega, Japón, Suiza, EE. UU, Liberia, Palau,
Camerún, Serbia y Portugal). La luz principal (L) de estos puentes tienen
valores que oscilan entre 44 metros y 241 metros.
4.1.2 1980-2000.
Se tienen datos geométricos de 48 puentes
diseñados y construidos durante estos años, pertenecientes a 16 países (España,
Francia, Alemania, Noruega, Escocia, Bangladesh, Grecia, Suiza,
EE. UU, Suecia, Finlandia, Tailandia, Polonia, Croacia, Reino Unido y Vietnam).
La luz principal (L) de estos puentes tienen valores que oscilan entre 30
metros y 301 metros.
4.1.3 2000-2016.
Se tienen datos geométricos de 27 puentes
diseñados y construidos durante estos años, pertenecientes a 13 países (España,
Colombia, Francia, Alemania, Noruega, Bolivia, Turquía, Grecia, Malasia,
República Checa, Abu Dhabi y Australia). La luz principal (L) de estos puentes
tienen valores que oscilan entre 44 metros y 298 metros.
4.2 Luz libre
Se presentan los datos clasificados por
magnitud de luz libre. Se tiene valores de hasta 301 metros y se presentan
fraccionados en grupos de cada 50 metros. Estos son:
•
<50
•
50-100
•
100-150
•
150-200 • 200-250
•
250-301
4.2.1 <50m.
Se tienen datos geométricos de 4 puentes
con una luz libre inferior a 50 metros, pertenecientes a 3 países (Francia,
Alemania, Tailandia). Estos puentes fueron construidos entre los años 1977 y
2004.
4.2.2 50m-100m.
Se tienen datos geométricos de 44 puentes con
una luz libre de entre 50 metros y 100 metros, pertenecientes a 9 países
(España, Francia, Colombia, Alemania, Suiza, Malasia, Polonia, Croacia,
Portugal). Estos puentes fueron construidos entre los años 1957 y 2007.
4.2.3 100m-150m.
Se tienen datos geométricos de 46 puentes
con una luz libre de entre 100 metros y 150 metros, pertenecientes a 16 países
(España, Francia, Colombia, Alemania, Noruega, Bolivia, Bangladesh, Suiza, EE.
UU, Suecia, Liberia, Finlandia, Tailandia, República Checa, Camerún, Vietnam).
Estos puentes fueron construidos entre los años 1967 y 2011.
4.2.4 150m-200m.
Se tienen datos geométricos de 17 puentes
con una luz libre de entre 150 metros y 200 metros, pertenecientes a 8 países
(España, Francia, Colombia, Alemania, Noruega, Suiza, Abu Dhabi, Turquía).
Estos puentes fueron construidos entre los años 1968 y 2014.
4.2.5 200m-250m.
Se tienen datos geométricos de 11 puentes
con una luz libre de entre 200 metros y 250 metros, pertenecientes a 9 países
(Francia, Alemania, Escocia, Japón, Grecia, EE. UU, Palaus, Serbia, Reino
Unido). Estos puentes fueron construidos entre los años 1960 y 2004.
4.2.6 250m-301m.
Se tienen datos geométricos de 3 puentes
con una luz libre de entre 250 metros y 301 metros, siendo esta la luz mayor de
las estudiadas; pertenecientes a 2 países (Noruega y Australia). Estos puentes
fueron construidos entre los años 1998 y 2007.
4.3 Países
Se presentan los datos clasificados por el
país donde se haya construido. Se forman cuatro grupos pertenecientes cada uno
a una nación distinta, debido al volumen considerado de datos de ese país; y un
quinto grupo donde se engloban el resto de puentes del resto del mundo. Estos
son:
•
Alemania
•
Colombia
•
Francia
•
España
•
Resto del mundo
4.3.1 Alemania.
Se tienen datos geométricos de 12 puentes
en Alemania, con una luz libre (L) entre 40 metros a 208 metros.
Pertenecen al periodo temporal de los años
1960-2004.
4.3.2 Colombia.
Se tienen datos geométricos de 7 puentes en
Colombia, con una luz libre (L) entre 62 metros a 200 metros.
Pertenecen al periodo temporal de los años
1975-2007.
4.3.3 Francia.
Se tienen datos geométricos de 53 puentes
en Francia, con una luz libre (L) entre 30 metros a 242 metros.
Pertenecen al periodo temporal de los años
1960-2011.
4.3.4 España.
Se tienen datos geométricos de 15 puentes
en España, con una luz libre (L) entre 80 metros a 190 metros.
Pertenecen al periodo temporal de los años
1972-2014.
4.3.5 Resto del mundo.
Se tienen datos geométricos de 38 puentes
en Noruega,
Escocia, Japón, Bolivia, Bangladesh,
Turquía, Grecia, Suiza, EE. UU, Suecia, Liberia, Malasia, Finlandia, Palau,
Tailandia, Polonia, Croacia, República checa, serbia, Portugal, Camerún,
Portugal, Abu Dhabi, Australia, Reino Unido y Vietnam. Pertenecen al periodo
temporal de los años 1969-2008.
4.4 Árbol lógico
Se presenta en la figura 16 un árbol lógico
donde se sintetiza la forma en la que se han discretizado los datos tratados.
Figura 16. Árbol lógico referente a los datos de estudio.
Fuente. Elaboración propia.
5. ANÁLISIS ESTADÍSTICO
Se realiza un análisis estadístico de los
datos pertenecientes a los puentes presentados. Las operaciones a las que han
sido sometidos los grupos de datos son las siguientes, mostradas a continuación
en orden cronológico: • Desviación estándar (σ)
•
Descarte de los de fuera de rango
•
Regresión lineal y límites resultantes de
aplicación
•
Comparativa con los conceptos clásicos de L/20 y
L/50
A continuación, a modo de ejemplo
ilustrativo de lo anterior; se muestra este proceso para el grupo L/H, de los
años 1960-1980 dentro de la discretización cronológica de los datos.
5.1 Desviación estándar
En el grupo de datos de L/H de los años
1960-1980 de la discretización cronológica de los datos se aplica el
5.2 Descarte de los de fuera de rango
Continuando con el ejemplo de cómo se ha
estudiado este grupo de datos, se eliminan los puentes que la desviación
estándar (σ) ha dejado fuera de rango. En este caso, de los 50 puentes se van a
estudiar 43 y se dejan fuera de estudio 7.
5.3 Regresión lineal y límites resultantes de aplicación
Una vez eliminados los datos de los puentes
desechados por la desviación estándar σ se grafica la relación que se está
estudiando. Continuando con este ejemplo ilustrativo, se grafica en la figura
18 de forma paramétrica L/H de los 43 puentes considerados.
Además de eso se establece una recta de
regresión lineal de los datos. Con el valor de la desviación estándar σ se
fijan límites superior e inferior, quedando representado el rango de aplicación
de este grupo de datos.
(b) los límites superior e inferior del
rango estudiado aplicando la desviación estándar σ mencionada y la ecuación que
los describe, (c) la línea de regresión lineal y la ecuación que la describe y
(d) la correlación entre los datos estudiados. Fuente.
Elaboración propia.
5.4 Comparativa con los conceptos clásicos de L/20 y
L/50
Se ha hallado la relación entre el valor
estudiado y el valor L del puente. En este caso de ejemplo se estudia la
relación entre L/H y L. Como H corresponde al valor del canto del tablero en
los apoyos, se procede a compararlo con el correspondiente L/20.
En este caso se observa en la figura 19 que
los puentes estudiados varían su relación L vs L/H entre los valores de L/15.25
y L/21.90.
Se presenta a continuación el análisis de
resultados del estudio estadístico anterior. Se muestra según los tres
apartados ya comentados; Cronología, Luz libre y Países.
6.1 Cronología
Según la figura 20, los valores extremos de
la relación L vs L/H con el paso del tiempo se van alejando del clásico L/20.
El rango de amplitud variable de H en relación a L en 1980-2000 aumentó por su
límite superior, manteniendo el inferior en el mismo valor, y en la actualidad
(2000-2016) el límite superior ha descendido, pero el inferior también, como se
demuestra en la gráfica siguiente.
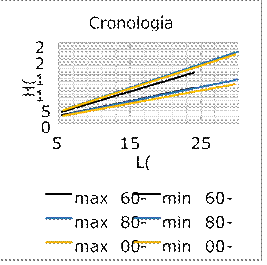
Figura 20. Gráfico de la variabilidad
del rango de H frente a L, donde se muestran los límite superior e inferior de
este valor en (a) los años 1960-1980, (b) los años 1980-2000, y (c) los años
2000-2016. Fuente. Elaboración propia.
Los valores extremos de la relación L vs
L/h, como se aprecia en la figura 21; con el paso del tiempo se van alejando
del clásico L/50. El rango de amplitud variable de h en relación a L en
1980-2000 aumentó tanto por su límite superior como por el inferior, y en la
actualidad (2000-2016) el rango de amplitud de h ha crecido. Esto es que ha
aumentado su límite superior y ha disminuido su límite inferior, como se
demuestra en la siguiente gráfica. Es importante mencionar que hoy en día se
manejan valores del rango L/68-L/30, muy lejos del clásico L/50.
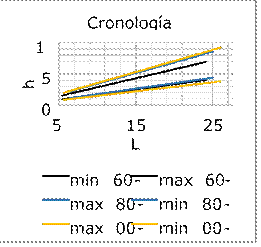
Figura 21. Gráfico de la variabilidad
del rango de h frente a L, donde se muestran los límite superior e inferior de
este valor en (a) los años 1960-1980, (b) los años 1980-2000, y (c) los años
2000-2016. Fuente. Elaboración propia.
Según se aprecia en la figura 22, los valores
extremos superiores de la relación L vs h/H con el paso del tiempo han ido
variando, pero no así los inferiores, que se consideran similares en las tres
épocas estudiadas. En la época de los años 1980-2000 el valor superior se
redujo, haciendo los valores de h y H más similares entre sí; pero finalmente
hoy en día puede considerarse (como se aprecia en la figura 21) que se ha
vuelto a los valores de la primera época estudiada (1960-1980).
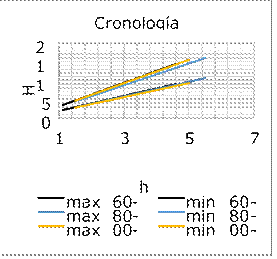
Figura 22. Gráfico de la variabilidad
del rango de H frente a h, donde se muestran los límite superior e inferior de
este valor en (a) los años 1960-1980, (b) los años 1980-2000, y (c) los años
2000-2016. Fuente. Elaboración propia.
A continuación, se exponen la figura 23, la
figura 24 y la figura 25, donde se muestran las gráficas de la tendencia de
variación del rango de las relaciones L/H, L/h y h/H respectivamente, a lo
largo de las épocas estudiadas.
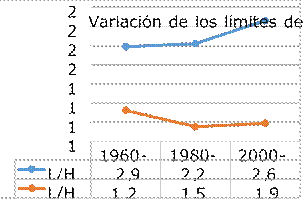
Figura 23. Gráfico de la evolución del
rango de L/H en las épocas estudiadas. Fuente. Elaboración propia.
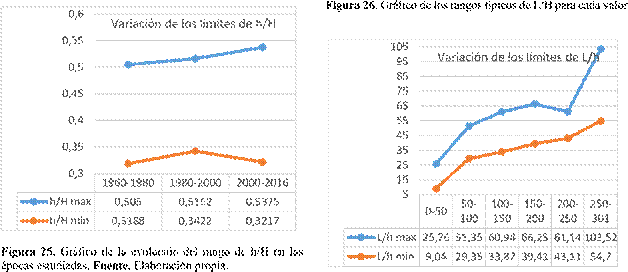
Puede concluirse que los rangos se van
ampliando conforme avanza la historia, ya que también ha ido cambiando la forma
de concebir este tipo de estructuras.
6.2
Luz libre
Se han divido los datos en grupos cada 50
metros de luz libre para valores inferiores a 301m.
Debe remarcarse que los resultados del
estudio arrojan que este tipo de puentes no son apropiados para luces menores
de 50m, así como para luces mayores de 250m, debido a que resultan relaciones
L/H, L/h y h/H fuera de los rangos normales.
A continuación, se muestran la figura 26,
la figura 27 y la figura 28, donde se exponen las gráficas de las relaciones
estudiadas para cada grupo de datos.
de L estudiado. Fuente. Elaboración
propia.
Figura 27. Gráfico de los rangos típicos
de L/h para cada valor de L estudiado. Fuente. Elaboración propia.
Figura 28. Gráfico de los rangos típicos
de h/H para cada valor de L estudiado. Fuente. Elaboración propia.
Como se mencionó, queda demostrado que para
este tipo de puentes el rango aconsejable de luces es de entre 50m y 250m. Para
valores de luz libre fuera de ese rango, no resultan eficientes, como muestran
las relaciones estudiadas en los tramos inferiores a 50m y de 250m a 301m.
Son ineficientes a luces menores de 50
metros porque en tan poca luz libre debe generar la curvatura estudiada, y eso
lleva a valores no óptimos de H y h. Por otro lado, debido a la gran longitud
de luces mayores a 250 metros, la relación h/H resulta entre 1/3 y 1/4,
mientras que en valores de L normales esta relación arroja resultados entre 1/3
y 1/2.
Respecto a las relaciones L/H y L/h se
observa como en el rango descrito como típico de L se mantienen cerca de los
clásicos L/20 y L/50, mientras que fuera de ese rango de L se distorsionan
totalmente, dando lugar por ejemplo a L/1.64 para L/H o L/103.52 para L/h.
6.3
Países
Se han divido los 124 puentes según los
países más representativos entre los que se encuentran. Se exponen los valores
de las relaciones estudiadas.
En la figura 29 se presenta la gráfica de
los valores por países de L/H, donde se ve que Colombia tiene el menor valor de
H respecto a L, es decir; contempla valores de H muy bajos. En el caso opuesto
se encuentra Alemania, con valores de H altos en relación a L.
Figura 29. Gráfico de la variabilidad
del rango de H frente a L, donde se muestran el límite superior e inferior de
este valor en (a) Alemania, (b) Colombia, (c) España, (d) Francia y (e) resto
del mundo. Fuente. Elaboración propia.
En la figura 30 se presenta la gráfica de
los valores por países de L/h, donde se ve que Colombia tiene el menor valor de
h respecto a L, es decir; contempla valores de h muy bajos. En el caso opuesto
se encuentra Alemania, con valores de h altos en relación a L.
Figura 30. Gráfico de la variabilidad
del rango de h frente a L, donde se muestran el límite superior e inferior de
este valor en (a) Alemania, (b) Colombia, (c) España, (d) Francia y (e) resto
del mundo. Fuente. Elaboración propia.
Se obtiene que Colombia tiene puentes muy
esbeltos, (valores de H y h bajos) frente a Alemania, que tiene los valores más
altos de H y h frente a la luz de los países estudiados.
En la figura 31 se presenta la gráfica de
los valores por países de h/H, donde se ve que Colombia y España tienen un
rango de valores de h/H pequeño; es decir, no hay mucha variación entre los
valores de h y H de sus puentes. El rango más amplio por otro lado, lo tiene
Francia.
7. CONCLUSIONES
Se estudiaron 124 puentes de voladizos
sucesivos in situ, construidos en 29 países. Se estudiaron las diferentes
metodologías para el predimensionamiento. Se realizó un análisis estadístico y
se obtuvieron gráficas paramétricas de las que se obtuvieron las siguientes
conclusiones.
Del estudio de las diferentes teorías de
predimensionamiento a lo largo de distintas épocas, se concluye que se tiende a
aumentar la distancia entre almas y a aumentar el espesor de la losa superior e
inferior. Además, se tiende a que la diferencia de áreas de la sección transversal
asociada a los puntos donde se define H y h sea menor. Considerando, como es lo
más habitual; que no varían los espesores a lo largo de la sección transversal,
se obtiene que lo que varía es la altura de la viga. Esto lleva a concluir que
se tiende a disminuir diferencia de altura de viga entre las secciones H y h,
es decir; a una curvatura menor de la sección longitudinal.
Figura 31. Gráfico de la variabilidad
del rango de h frente a H, donde se muestran los límites superiores e
inferiores de este valor en (a) Alemania, (b) Colombia, (c) España, (d) Francia
y
(e) resto del mundo. Fuente.
Elaboración propia
En el análisis cronológico se concluye que
los valores extremos de la relación L vs L/H con el paso del tiempo se van
alejando del clásico L/20. Hoy en día el valor de H frente a L puede variar en
un rango más amplio que en la época de las primeras estructuras estudiadas.
Igualmente, los valores extremos de la
relación L vs L/h con el paso del tiempo se van alejando del clásico L/50. En
la actualidad el rango de amplitud de h ha crecido. Se debe mencionar que hoy
en día se manejan valores del rango L/68-L/30, muy lejos del clásico L/50.
Del estudio por tramos se concluye que este
tipo de puentes no son adecuados para luces menores de 50 metros, ni para
mayores de 250, ya que resultan valores de las relaciones L/H y L/h anormales y
lejos de lo óptimo. En los puentes de luz menor de 50 metros la curva debe
generarse en esa longitud, que resulta insuficiente. En los puentes de luz mayor
a 250 metros debido a su gran longitud, la relación h/H resulta entre 1/3 y
1/4, mientras que, en valores de L normales, esta relación arroja resultados
entre 1/3 y 1/2.
Respecto a las relaciones L/H y L/h se
observa como en el rango anteriormente descrito de valores de L entre 50m-250m
se mantienen cerca de los clásicos L/20 y L/50, mientras que fuera de ese rango
de L se distorsionan totalmente, dando lugar por ejemplo a L/1.64 para L/H o
L/103.52 para L/h. Por eso este rango de luz libre se considera como óptimo
para este tipo de puentes.
Del estudio por países se concluye que
Colombia contempla valores de H y h muy bajos, en contraposición a Alemania,
que es el país con valores H y h más altos. Además, se observa que Colombia y
España tienen el rango de h/H más pequeño, es decir; su H y h no varía mucho.
Esta similitud se debe en parte a las obras ejecutadas en Colombia por empresas
españolas. En el lado opuesto está Francia. Esta diferencia se da porque
históricamente Francia ha sido muy continuista con su propia cultura
ingenieril, sin tener en cuenta influencias externas.
8. AGRADECIMIENTOS
Se agradece el apoyo logístico y económico
de Estructuras & Sísmica S.A.S al desarrollo de esta investigación.
9. REFERENCIAS
Obras de paso de nueva construcción,
Ministerio de
Fomento de España, Madrid, España, 2000
D. F. Cetina, N.E. Ovalle, “Evaluación del
proceso constructivo en el comportamiento estructural de un puente construido
por voladizos sucesivos,” Tesis de Grado, Facultad de Ingenierías
Físico-Mecánicas, Universidad Industrial de Santander, Bucaramanga, 2011.
Prestressed concrete bridges built using
the cantiliver method-SETRA, Ministere de l´Ecologie du
Developpment et de l´Amenagement durables,
Francia,
2003
W Podolny y J.M. Muller “Prestressed
concrete bridges and segmental construction” en Construction and desing of
prestressed concrete segmental bridges, 1a ed.
Canada:Wiley-Interscience, 1982.
W Podolny y J.M. Muller “Cast-in-place
balanced cantiliver girder bridges” en Construction and desing of prestressed
concrete segmental bridges, 1a ed.
Canada:Wiley-Interscience, 1982.
C. F. Casado, “Ejecición de puentes
pretensados por voladizos sucesivos,” Informes de la construcción, vol.
16, no. 158, Mar. 1964
J. Mathivat “Construcción en voladizo por
hormigonado in-situ de dovelas” en Construcción de puentes de hormigón
pretensado por voladizos sucesivos, 1a ed. Barcelona, España:Editores técnicos
asociados, 1980.
Precast segmental box girder bridge manual,
PCI,
EE.UU, 1978
J. Mathivat “Concepción y dimensionamiento
de tableros” en Construcción de puentes de hormigón pretensado por voladizos
sucesivos, 1a ed. Barcelona, España:Editores técnicos asociados, 1980.
J. Manterola “Construción de puentes” en
Puentes. Apuntes para su diseño y construcción, 1a ed. Madrid, España:Colección
Escuelas, 2006.
F. A. Ariñez, “Criterios para la
optimización del predimensionamieto de puentes de sección cajón,” Tesis de
Máster, Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos,
Universidad Politécnica de Madrid, Madrid, 2012.
M. Aguiló, J. Manterola, M. Onzain.,J
Rui-Wamba Javier Manterola Armisén. Pensamiento y Obra, 1a ed.
Madrid, Fundación ESTEYCO, 2004.
C. Luna, “Análisis y dimensionamietno de
puentes construidos por avance de cimbra,” Trabajo Fin de Grado, Escuela
Técnica Superior de Ingenieros de Sevilla, Universidad de Sevilla, Sevilla,
2015.
M. L. Nancu, “Metodología para el Análisis
y Dimensionamiento de Puentes Construidos Evolutivamente mediante Avance por
Voladizos
Sucesivos,” Tesis de Grado, Escuela Técnica
Superior de Ingeniería, Universidad de Sevilla, Sevilla, 2011.
H. R. Higuita, “Diseño de puentes de
hormigón postensado construidos por voladizos sucesivos. Caso concreto de
aplicación,” Tesis de posgrado, Facultad Nacional de Minas, Universidad
Nacional de Colombia, Medellín, 1998.
Guide Specifications for Desing and
Construction of Segmental Concrete Bridges #2, American Association of State
Highway and Transportation Officials, US, 1999.
J. D. Honorio, “Conceptual design of
long-span cantilever constructed concrete bridges,” Tesis de Master, KTH,
Estocolmo, 2007.
M. G. Perdomo, “Estudio Comparativo de
Puentes Construidos por Voladizos Sucesivos,” Tesis de Master, Universitat
Poliécnica de Catalunya, Barcelona, 2011.
Structurae (2016). International Database
for Civil and Structural Engineering. Berlin, Alemania.
https://structurae.net/
A. M. Agredo Chavez et al., “Evaluación de
la rigidez a flexión de puentes de viga y losa en concreto presforzado a partir
de pruebas de carga. Caso de estudio: Puente La Parroquia vía La Renta - San
Vicente de
Chucurí,” UIS Ingenierías, vol. 15, no. 2,
pp. 145-159, Jul-Dic 2016.
MARTÍNEZ, Carolina, TORRES, Janneth y
MEJÍA, Ruby. Evaluación de la toxicidad de
un residuo industrial estabilizado/ solidificado con cemento portland.
Rev.UIS.Ingenierías, 2014, vol.13, n.1, p.p 47-54.