INTRODUCCIÓN
El
mecanismo plano de cuatro barras es utilizado en diferentes ramas de la
Ingeniería como solución a problemas de generación de movimiento tales como
sistemas articulados para la puerta de equipaje de vehículos comerciales
(Baykus, E., et al. 2011) como base para un modelo en Ingeniería Biomédica
(Farhat, N., et al. 2011), y otras aplicaciones utilizadas ampliamente en la
industria (Roy, L., et al., 2008; Thakare y Panda, 2012). Para el estudio del
mecanismo plano de cuatro barras también han sido desarrolladas varias
aplicaciones de computadora para su análisis cinemático (Pucheta, Cardona,
2004; Vásquez, Ramírez, 2006; Ruíz, Valencia, 2008; Norton, 2009), algunos de
los cuales también incluyen los aspectos cinemáticos de mecanismos de levas de
disco (Hoorfar, M., et al. 2007; Norton, 2009). Un objetivo fundamental de la
Cinemática, es diseñar los movimientos deseados de las partes mecánicas por medio
de la síntesis de mecanismos, para luego calcular matemáticamente las
posiciones, velocidades y aceleraciones de cada parte del elemento. El
eslabonamiento plano de cuatro barras es el mecanismo articulado más simple
posible para movimiento controlado con un solo grado de libertad, razón por la
cual es usualmente considerado como candidato en la solución de problemas de
generación de movimiento. Varios autores se enfocan en la síntesis de
mecanismos para resolver tales problemas (Linares, Augusto, 2007; Peón, R., et
al, 2009), incluso haciendo uso de software para satisfacer los requerimientos
cinemáticos (Pucheta, Cardona, 2004). Una vez que la síntesis del mecanismo ha
sido realizada, la naturaleza de su movimiento debe ser analizada. Es necesario
conocer las fuerzas, estáticas y dinámicas, para calcular los esfuerzos. El
ingeniero de diseño debe garantizar que el mecanismo o máquina propuesta no
fallará en condiciones de operación. Por lo tanto, los esfuerzos en los
materiales deben mantenerse por debajo de los niveles permisibles (Portilla,
É., et al. 2010). Para calcular los esfuerzos es necesario conocer las
aceleraciones de sus elementos, las cuales varían con cada posición del
mecanismo, por lo cual es menester un correcto análisis de posición del mecanismo.
Muchos
softwares educativos o con fines didácticos en el área de Teoría de Mecanismos
y Máquinas que abarcan el análisis de posición permiten graficar mecanismos de
cuatro barras en diferentes posiciones (Barker, 1985; Vásquez, Ramírez, 2006;
Ruíz, Valencia, 2008), pero requieren licencia de usuario lo cual le dificulta
el acceso a la herramienta didáctica al estudiante, o en algunos casos la
versión estudiantil es muy limitada en opciones. En este artículo se presenta
un modelo computacional interactivo que permite el análisis cinemático para
mecanismos planos de cuatro barras con cuatro juntas de revoluta (2D-RRRR).
Utilizando Matlab®, se crea una interfaz gráfica amigable con un alto grado de
interactividad, la cual es capaz de validar la longitud de los eslabones,
calcular la posición, velocidad y aceleración de los mismos, graficar el
mecanismo y simular un ciclo completo del mecanismo.
GENERALIDADES DE LOS
MECANISMOS DE CUATRO BARRAS
La Figura
1(a) muestra la representación simplificada del mecanismo de cuatro barras con
cuatro juntas de revoluta y cuatro eslabones (eslabón 1 es la bancada), cuya
movilidad es igual a uno de acuerdo con la Ley de Grüebler (Norton, 2009), es
decir, solo se requiere mover un elemento de los elementos 2, 3 o 4 para
conocer en todo momento el movimiento que describirá cada eslabón móvil. Una de
las mayores ventajas y que ha favorecido el amplio uso de este mecanismo en
tareas cinemáticas planas es precisamente el requerir un único actuador, de ahí
su importancia en el campo de Teoría de Mecanismos y Máquinas (Farhat, N., et
al. 2011). La realización de una interfaz para este mecanismo requiere del
estudio de la cinemática de posición, velocidad y aceleración del mecanismo,
además del estudio de las condiciones de movilidad.
2.1 Generalidades Cinemáticas
La Figura
2(a) presenta el lazo vectorial asociado a la nomenclatura del mecanismo
presentada en la Figura 1(b). De la Figura 2(a), la ecuación vectorial resultante
está dada por la Ecuación (1), la cual genera las ecuaciones de las componentes
dadas en las Ecuaciones
donde ci = cosθi y si = sinθi. Asumiendo que el ángulo conocido o la entrada es el ángulo θ2, la solución de las Ecuaciones (2) y (3) se propone introduciendo las
identidades de la tangente del ángulo medio para obtener
donde A = L1s1 - L2s2, B = L1c1 - L2c2,
Dada la
naturaleza cuadrática de la solución presentada en las Ecuaciones (4) y (5),
ello implica dos posibles configuraciones físicas del mecanismo, ilustradas en
la Figura 2(b). Para la cinemática de velocidad se condiciona constante la
velocidad de la entrada, , lo cual implica que su aceleración
es igual a cero. Derivando una vez las
Ecuaciones (2) y (3) para solucionar la cinemática de velocidad, y por segunda
vez para resolver la cinemática de aceleración, se obtienen, respectivamente,
las soluciones
donde sk-m = sin(θk-θm).
Figura 1. Mecanismo plano de cuatro
barras con juntas de revoluta
2.2 Generalidades de Movilidad
Partiendo
del concepto de inversión cinemática de un mecanismo, que es la configuración
creada por el cambio de la conexión a tierra de un eslabón diferente en la
cadena cinemática, la condición de Grashof (Peón, R., et al. 2009) es la
relación que predice el comportamiento de rotación de las inversiones de un
mecanismo de cuatro barras basado en las longitudes de los eslabones. Sea S:
longitud del eslabón más corto, L: longitud del eslabón más largo, P y Q:
longitud los eslabones restantes, si se cumple la condición S+L ≤ P+Q, entonces
el eslabonamiento se clasifica como tipo Grashof y al menos un eslabón será
capaz de realizar una revolución completa con respecto al plano de bancada,
marco fijo o tierra. Si la desigualdad no es cierta, entonces el eslabonamiento
es No Grashof, lo cual implica que ningún eslabón será capaz de realizar una
revolución completa con respecto a cualquier otro eslabón. Las inversiones se
definirán con respecto al eslabón más corto, y los casos de movimiento se
presentan a continuación.
2.2.1 Mecanismo
de cuatro barras Clase I, S + L < P + Q. Si se considera como bancada
cualquier eslabón adyacente al más corto, Figura 3(a), se obtiene un mecanismo
manivela-balancín, donde el eslabón más corto girará por completo y el otro
eslabón oscilará pivotado a la bancada. Si se fija el eslabón más corto, se
obtendrá un doble-manivela, Figura 3(b), en la que ambos eslabones pivotados a
la bancada realizan revoluciones completas, así como lo hace el acoplador. Si
se fija el eslabón opuesto al más corto, se obtendrá un doble-balancín de
Grashof, Figura 3(c), en el que ambos eslabones pivotados a la bancada oscilan
y sólo el acoplador realiza una revolución completa.
2.2.2 Mecanismo de cuatro barras Clase II, S +
L > P + Q o triple balancín. En los mecanismos planos de cuatro barras Clase II, todas las
inversiones serán balancines triples, y ningún eslabón puede girar por completo
sin importar que eslabón sea escogido como el eslabón fijo o bancada, Figura
3(d).
2.2.3 Mecanismo de cuatro barras Clase III, S + L = P + Q. Los mecanismos planos de cuatro
barras Clase III son conocidos como caso especial de Grashof y también como
cadena cinemática de clase III, todas las inversiones serán doble-manivelas o
manivelabalancín, pero tendrán puntos de cambio dos veces por revolución de la
manivela de entrada cuando todos los eslabones se vuelven colineales. En estos
puntos de cambio el comportamiento de salida se volverá indeterminado. La
Figura 4 presenta un esquema de la clasificación completa de mecanismos de
cuatro barras basada en un sistema desarrollado por Barker (1985).
Figura 2. Lazo vectorial y
configuraciones de la solución
Figura 3. Tipos de mecanismos Grashof (unidades en cm)
Figura
4. Esquema de clasificación de mecanismos planos de cuatro barras
|
El criterio
de Grashof asegura que para que los cuatro eslabones se ensamblen, el más largo
debe ser más corto que la suma de los otros tres, es decir L < S + P + Q, lo
cual es la base para la validación de las longitudes entradas al programa. Si L
= S + P + Q, entonces los eslabones pueden ser ensamblados pero no se moverán,
así que esta condición proporciona un criterio para separar las regiones de no
movilidad de las regiones que permiten movimiento.
3. INTERFAZ GRÁFICA DESARROLLADA
La
metodología empleada para el desarrollo de la interfaz grafica fue la de “marco
de trabajo”, la cual es usada para
estructurar, planear y controlar el proceso de desarrollo en sistemas de
información. El enfoque que se le dio al desarrollo de la interfaz fue un
modelo en cascada, el cual es un proceso secuencial en el que los pasos de
desarrollo son vistos hacia abajo, a través de las fases de análisis de las
necesidades, el diseño, su implementación, pruebas (validación) e integración.
El GUI se desarrolló usando la herramienta GUIDE (Graphical User Interface Development Enviroment) de Matlab® (The
MathWorks, 2012). La interfaz se dividió en cuatro secciones principales o
paneles: Presentación, Parámetros de Entrada, Funciones y Parámetros de Salida,
presentadas a continuación.
3.1 Interactividad de la Interfaz
El panel de
“Parámetros de entrada” mostrado en la Figura 5(a) presenta una imagen
ilustrativa de un mecanismo plano de cuatro barras RRRR, en la cual se muestra
la nomenclatura usada para identificar eslabones, ángulos, y demás parámetros
que ayudan al usuario a familiarizarse con la interfaz.
Este panel
también contiene las cajas de edición para introducir los parámetros de entrada
(Longitudes de eslabones, ángulos, etc.). En este punto de uso de la interfaz,
la entrada de datos se hace mediante teclado. La ley de Grashof se utiliza
para evaluar que las dimensiones dadas
satisfagan un mecanismo y para clasificar el mecanismo al presionar el botón
“Calcular”, Figura 5(b).
3.2 Características de la
Interfaz
Idioma. La
interfaz cuenta con un menú contextual que permite modificar su idioma a
español o inglés, Figura 5(a). Se incluyó la opción del inglés para contribuir
con uno de los objetivos del programa de Ingeniería Mecánica de la Universidad
del Atlántico, como es fortalecer la enseñanza de este idioma extranjero. La
Figura 7 presenta el aspecto de la interfaz en el idioma inglés.
Figura 5. Bloques de parámetros de entrada y de funciones
Arrastre de
juntas. Figura 5(b), cuando esta casilla se encuentra activa, el usuario podrá
modificar la longitud y posición de los eslabones con ayuda del mouse, haciendo
click sostenido en las juntas de revoluta del mecanismo calculado, como se
ilustra en la Figura 6. Esta función habilitada para la interfaz constituye una
de las principales características de amigabilidad para el usuario. Facilita la
edición del mecanismo alternando entre los diferentes tipos (Grashof, No
Grashof, tipos I, II y II) y modificando los parámetros de entrada y salida en
tiempo real.
En el panel
de funciones, subpanel de Animación en la Figura 5(b) se introduce también el
número de ciclos que se desee animar el mecanismo calculado.
La
velocidad del animación también se modifica a través de un deslizador para
incrementar o disminuir la rapidez de la animación, la cual puede ser iniciada,
pausada o reanudada con los botones Play y Pause.
Cinemática
de punto. Figura 5(b), al habilitar esta casilla, se le permite al usuario
seleccionar con el puntero del mouse un punto de cualquier eslabón del
mecanismo, y graficar los valores de velocidad y aceleración (angular y
absoluta) de dicho punto dependiendo de la casilla que se encuentre habilitada
en el panel de gráfica cinemática.
Mensajes de
error. La interfaz cuenta con funciones de validación de los parámetros de
entrada, las cuales permiten al usuario verificar que los datos ingresados sean
correctos, de lo contrario se generarán mensajes explicando el error y
sugiriendo la solución. La validación no permite que el usuario introduzca
distancias negativas o caracteres diferentes a los numéricos.
Parámetros
de salida. Es la sección Output
Parameters en la Figura 7, y presenta las salidas tanto de texto como
gráficas generadas.
Relación
color–eslabón. Para facilitar la identificación de los eslabones del mecanismo
calculado, la interfaz relaciona los colores de los eslabones del mecanismo
dibujado con los colores de las cajas de edición, ver Figura 7.
Figura 6. Cambio de longitudes y
geometría con arrastre de juntas
Figura 7. Aspecto de la interfaz desarrollada en el
idioma Inglés
|
4. RESULTADOS
4.1 Opinión de los Usuarios
Se realizó
una presentación del GUI a los estudiantes del laboratorio de la asignatura
“Teoría de Mecanismos y Máquinas” (2012-1, 20 estudiantes y 2012-2, 15
estudiantes) de la Universidad del Atlántico, seguida de la encuesta mostrada
en la Figura 8. Las preguntas se agruparon en tres aspectos: Funcionalidad,
Manipulación y Diseño de la GUI, Figura 8(a). Los resultados muestran un alto
nivel de aceptación, situando la GUI como una herramienta útil, Figura 8(b).
También se tomaron en cuenta algunas observaciones realizadas por los
estudiantes para la mejora de la interfaz, sugerencias tales como:
Figura 8. Encuesta realizada a
estudiantes del laboratorio del curso Teoría de Mecanismos y Máquinas
|
“Se podrían reubicar los gráficos de acuerdo al
tamaño de la pantalla”; “Cuando los parámetros de entrada no son válidos, que
muestre un mensaje explicando el error”; “Aumentar el tamaño de la animación”;
“Que la interfaz indique el tipo de triple balancín (1, 2, 3, 4)”.
4.2 Validación de Resultados
Para
verificar los resultados de la cinemática posición, se alimentó la interfaz con
los datos de varios problemas de libros de texto, especialmente del autor
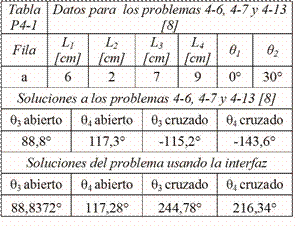
Norton (2009), muy reconocido en la Academia. La Tabla 1 presenta los
resultados de Norton (2009) y de la interfaz para un problema específico. Hay
concordancia en los resultados obtenidos. Similarmente, se validaron los resultados
de velocidad y aceleración contra problemas resueltos de la misma referencia,
presentados en las Tablas 2 y 3, mostrando prácticamente el mismo resultado en
cada caso.
Tabla 1. Validación análisis de posición
Tabla
2. Validación análisis de velocidad
Tabla 3. Validación análisis de
aceleración
4.3 Validación de Resultados, FOURBAR – Student Edition
Se presenta un mecanismo de estudio para
comparar el GUI con el software FOURBAR Student Edition, CD es gratuito con la
compra del libro de texto Norton (2009). Los datos de entrada se resumen en la
Tabla 4. La solución hallada utilizando FOURBAR se presenta en la Figura 9 y la
solución generada utilizando la interfaz en la Figura 10, obteniendo en ambos
casos la misma solución gráfica, sin embargo la aplicación FOURBAR no muestra
como datos de salida los ángulos θ3 y θ4. En cuanto a la interactividad, la GUI propuesta permitió el cambio de
longitudes y ángulos bien sea a través de teclado en el bloque de parámetros de
entrada, o arrastrando cada junta presionando el ratón del computador,
cambiando así de manera inmediata las longitudes de los elementos y/o ángulos
de configuración. Además, la interfaz desarrollada permite una rotación
completa de la manivela en la simulación, mientras que FOURBAR solo permite
visualizar media revolución de la manivela.
Tabla 4. Datos de mecanismo (Esl:
Eslabón)
Figura 9. Solución al ejemplo de
la sección 4.3 utilizando FOURBAR Student Edition (Norton, 2009)
Figura 10. Solución al ejemplo de
la sección 4.3 utilizando la herramienta desarrollada
|
|
|
4.4 Caso de Aplicación de Helicóptero
Tragamonedas
Se resuelve un caso de aplicación adaptado del libro de texto de autor
Myszka (2012). “El motor de la diversión del traga monedas de la Figura 11 gira
a 90 rpm, constante (antihorario). ¿Qué aceleración angular experimentaría un
niño en el instante en que la manivela tiene un valor de 30°? Alimentando la
interfaz con los datos del problema se obtiene inicialmente la clasificación
del mecanismo: Grashof biela-manivela, Figura 12. La interfaz también arroja la
velocidad y aceleración angular máximas a la cual está sometido el caballo:
2.79259 rad/s y 48.3 rad/s2, respectivamente, para el seguidor
(L = 762 mm) y para un ángulo de la manivela de aproximadamente 75°, Figura 12.
Figura 11. Helicóptero
tragamonedas, medidas en milímetros. (Adaptado de
Myszka, 2012)
Figura 12. Solución del
helicóptero tragamonedas utilizando la interfaz desarrollada
|
|
|
5. CONCLUSIÓN
Se reportó
el desarrollo y aplicación de una interfaz gráfica de usuario como una
herramienta para la enseñanza y el aprendizaje de la cinemática y la movilidad
de los mecanismos planos de cuatro barras. La idea nació ante el alto costo de
las licencias de software especializados y la limitación de las versiones
estudiantiles disponibles. El diseño de la interfaz tuvo en cuenta los
comentarios y sugerencias de los estudiantes de la asignatura de interés. Los
resultados obtenidos utilizando la interfaz desarrollada fueron validados
contra resultados de otros autores y con los resultados de otros softwares
similares.
Desde el
punto de vista de la interactividad, la interfaz propuesta permite la
modificación de las longitudes y orientación de los elementos del mecanismo,
tanto numéricamente a través del teclado, como gráficamente haciendo uso del
mouse del computador, sobre la interfaz desarrollada. Esta es una gran ventaja
en comparación con softwares disponibles. Estas cualidades, permiten que la
interfaz sea una herramienta fundamental para ser implementada dentro del
laboratorio de la asignatura “Teoría de Mecanismos y Máquinas” del programa de
Ingeniería Mecánica de la Universidad del Atlántico. El estudiante podrá
simular los diferentes cambios debido a las alteración es realizadas a la
longitud y orientación de las juntas de un mecanismo de cuatro barras.
El
desarrollo de la interfaz gráfica se convierte en un enlace entre los conceptos
teóricos y prácticos del análisis de mecanismos, mostrando de manera virtual su
comportamiento y permitiendo la observación de los fenómenos de una forma
versátil. Como futuro trabajo derivado es este proyecto se viene trabajando en
el desarrollo de una aplicación de Android que utilice el mismo principio y que
pueda ser adquirida a bajo costo por estudiantes de ingeniería y ser utilizada
como una guía de estudio.
6. AGRADECIMIENTOS
Los autores
agradecen el apoyo recibido de parte de la Vicerrectoría de Investigaciones de
la Universidad del Atlántico para la realización de este proyecto.
7. REFERENCIAS
BARKER, C. A complete classification of planar fourbar linkages. Mechanism and Machine Theory, 1985, vol. 20, núm. 6, pp. 535-554.
BAYKUS, E. et al. Design and kinematics analysis of a parallel mechanism to be utilized as a luggage door by an analogy to a four-bar mechanism. Engineering, 2011, vol. 3, núm. 4, pp. 421-441.
FARHAT, N. et al. A procedure for estimating the relevant forces in the human knee using a four-bar mechanism. Computer Methods in Biomechanics and Biomedical Eng., 2011, vol. 13, núm. 5, pp. 577-587.
HOORFAR, M. et al. Software demonstration of disc cam
mechanism for mechanical engineering education. Int. Journal of Mech.
Eng. Education,
2007, vol. 35, núm. 2, pp. 166-180.
LINARES, P;
AUGUSTO, H. Diseño óptimo de mecanismos
de cuatro barras para generación de movimiento con restricciones de montaje y
ángulo de transmisión. Director: Andrés Tovar [Tesis de Maestría].
Manizales, Colombia: Universidad Nacional de Colombia, 2007.
MYSZKA, D.
Máquinas y Mecanismos. 4ta ed. México: Pearson, 2012.
NORTON, R.
Diseño de maquinaria: Síntesis y análisis de máquinas y mecanismos. 4ta ed.
México: McGrawHill, 2009.
PEÓN, R. et
al. Síntesis dimensional óptima de un mecanismo planar RRRR usando algoritmos
genéticos. Ingeniería Revista Académica,
2009, vol. 13, núm. 3, pp. 5-16.
PORTILLA,
É. et al. Análisis cinemático y diseño de un mecanismo de cuatro barras para
falange proximal de dedo antropomórfico. Ciencia
e Ingeniería Neogranadina, 2010, vol. 20, núm. 1, pp. 45-59.
PUCHETA, M; CARDONA, A. Software para síntesis de mecanismos planos. Mecánica Computacional, 2004 , vol. 23, núm. 31, pp. 3369-3389.
ROY, L. et al. Analysis and synthesis of four-bar mechanism. Int. Journal of Theoretical and Applied Mech., 2008, vol. 3, núm. 2, pp. 171-186.
RUIZ, V; VALENCIA, N. Razonamiento cinemático en mecanismos eslabonados a través de ambientes computacionales. Tecné, Episteme y Didaxis: TED, 2008 , vol. 23, pp. 16-30.
THAKARE, P; HANDA, C. A generalized approach for kinematic analysis of four-bar chain mechanism using programming. Golden Research J., 2012, vol. 1, núm. 7 , pp. 1-4.
The MathWorks: Matlab GUI [web en línea]. <http://
www.mathworks.com/discovery/matlab-gui.html>. [ Consulta : 10-11-2012]
VÁSQUEZ, R;
RAMÍREZ, J. Software de simulación para un banco de mecanismos planos de cuatro
barras. XVI Muestra de Trabajos de
Ingeniería, Ingeniar Internacional, Editorial Universidad Pontificia
Bolivariana, Medellín, sept. 6-8 de 2006, vol. 6, pp. 25-136.