Resistencia de vigas esbeltas de acero inoxidable bajo cargas concentradas mediante análisis por elementos finitos

Strength of stainless steel girders under concentrated loads using finite element analysis

Asdrubal Ayestarán ¹, Carlos Graciano², Octavio Andrés González-Estrada³

¹Albatros Ingeniería, Quinta Las Palmas, Calle Sanz, Urb. Los Chaguaramos, Caracas, 1040, Venezuela.

Orcid: 0000-0001-9952-4282. Email: asdrubal.ayestaran@albatros-ing.com

2  Departamento de Ingeniería Civil, Universidad Nacional de Colombia, Medellín, 050034, Colombia.

Orcid: 0000-0003-0659-7963. Email: cagracianog@unal.edu.co

3 Grupo de Investigación en Energía y Medio Ambiente - GIEMA, Escuela de Ingeniería Mecánica, Universidad Industrial de Santander, Colombia. Orcid: 0000-0002-2778-3389. Email: agonzale@uis.edu.co

RESUMEN

El uso de acero inoxidable en estructuras ha cobrado fuerza en los últimos años debido a su gran relación costo-beneficio en el tiempo, brindando una gran protección a la corrosión, resistencia al fuego y una resistencia a la fluencia mayor que la brindada por los aceros estructurales de uso común en la industria. A pesar de este incremento en su uso todavía existe cierto grado de incertidumbre y desconocimiento de sus aplicaciones, pues los códigos de diseño de acero enfocan su atención principalmente en el acero estructural. Por lo tanto, en el presente trabajo se reportan los resultados de un estudio numérico de vigas esbeltas de acero inoxidable utilizado en puentes, sometidos a carga concentrada con el objeto de aumentar el estado del arte de esta aplicación en particular. En este trabajo, se elabora un modelo no lineal por elementos finitos tomando en cuenta el comportamiento no lineal del material y las imperfecciones geométricas iniciales. El modelo es validado utilizando datos experimentales encontrados en la literatura. Posteriormente se realizó un estudio paramétrico sobre la influencia de la relación de espesores (tf /tw) y relación de zona de carga - largo de viga (Ss /a) en la resistencia última. Finalmente, se obtiene que el uso del acero inoxidable presenta ventajas en su comportamiento post-crítico respecto a paneles geométricamente similares de acero estructural, permitiendo la optimización estructural de vigas esbeltas para puentes.

PALABRAS CLAVE: Vigas esbeltas, Carga concentrada, Acero inoxidable, Resistencia última.

ABSTRACT

The use of stainless steel in structures has gained momentum in recent years due to its good cost-benefit over time, protection to corrosion, fire resistance and creep resistance greater than that provided by structural steel commonly used in industry. Despite this increase in use there is still some degree of uncertainty and lack of knowledge regarding their application, as steel design codes focus mainly on structural steel. Therefore, the present work reports the results of the numerical study of thin stainless steel beams used in bridges, subjected to concentrated loads, in order to increase the state-of-the art of this particular application. A finite element model is constructed herein taking into account the non-linear behavior of the material and the initial geometric imperfections. This model is validated using experimental data found in the literature. Then, a parametric study on the influence of the thickness ratio (t_f /t_w) and load area – length of beam ratio (S_s /a) on the ultimate strength is performed. Finally, it is obtained that the use of the stainless steel presents advantages in its post-critical behavior with respect to geometrically similar panels of structural steel, allowing the structural optimization of girders for bridges.

KEYWORDS: Slender beams, concentrated load, stainless steel, ultimate strength.

INTRODUCCIÓN

Durante mucho tiempo se han utilizado aceros al carbono de alta resistencia en estructuras civiles como puentes y viaductos, debido principalmente a que su comportamiento estructural ha sido ampliamente estudiado y a su gran disponibilidad comercial. En la actualidad el acero inoxidable es una opción tentadora con fines estructurales debido a su alta resistencia mecánica frente a los aceros al carbono. A pesar de que los costos de producción asociados al acero inoxidable respecto al costo de aceros al carbono son mayores, éste presenta grandes ventajas como una gran resistencia a la corrosión, resistencia al fuego y estética [1] que el acero al carbono no puede proveer, minimizando los costos de mantenimiento y justificándose así la inversión inicial.

 Otra diferencia en particular del acero inoxidable sobre el acero al carbono es el comportamiento no lineal de su curva esfuerzo- deformación, pues ésta no presenta un valor marcado de fluencia, obteniéndose un mayor endurecimiento por deformación plástica y una mayor resistencia mecánica para deformaciones pequeñas. Sin embargo, su uso en estructuras ha estado limitado debido a la poca información que se encuentra en la literatura y que no existen metodologías de diseño en las cuales se aprovechen al máximo sus propiedades mecánicas. En el caso de diseño de estructuras de acero inoxidable, una norma utilizada es el Eurocódigo 3 Parte 1.4 [2], pero ésta solo establece pocos lineamientos con respecto a las propiedades del material a emplear y prácticamente su diseño está sujeto al Eurocódigo 3 Parte 1.5 [3], centrando éste su filosofía de diseño a estructuras de acero al carbono, por lo que los resultados obtenidos pueden ser conservadores, afectando entonces el aprovechamiento de sus propiedades mecánicas y por ende un uso no eficiente del material.

Un caso particular para el cual se usan vigas esbeltas de acero es en puentes. Si el método utilizado para instalar el puente es por medio de empujes sucesivos (Figura 1a), la viga estará sometida a una carga concentrada en la región del alma adyacente a los patines o soportes temporales durante su puesta en sitio, pudiendo presentarse una inestabilidad en el alma y una posible falla por pandeo localizado (Figura 1b).

Este tipo de falla por carga concentrada debe ser considerado y existen pocos casos reportados en la literatura donde se estudie este fenómeno en vigas esbeltas de acero inoxidable, como se muestra en la sección 2. Por lo tanto, en este trabajo se estudia la influencia del de diferentes parámetros geométricos sobre la carga concentrada máxima que puede soportar una viga esbelta de acero inoxidable usada en puentes. El estudio se realiza utilizando el método de los elementos finitos, según se expone en la sección 3, tomando en cuenta la no linealidad del material y las imperfecciones geométricas iniciales. Una vez que se construye el modelo numérico, éste es validado con resultados experimentales tomados de la literatura [4].

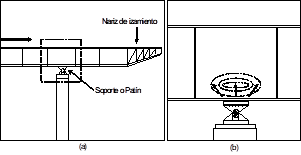
Figura 1. (a) Esquema del método de empujes sucesivos  y (b) Zona afectada por la distribución de esfuerzos en el alma de la viga por cargas concentradas.

Posteriormente, en la sección 4 se realiza un análisis paramétrico para determinar la influencia de lalgunos parámetros geométricos tales como la relación de espesores entre el alma y las aletas (t_f /t_w) y relación de zona de carga - largo de viga (S_s /a) sobre la carga máxima que la viga puede soportar. Adicionalmente, en la sección 5 se comparan las cargas máximas obtenidas mediante el modelo numérico con aquellas estimadas utilizando los códigos de diseño en acero [2,3]. Finalmente, los resultados revelan la necesidad de desarrollar una metodología de cálculo adecuada para la estimación de la carga concentrada máxima de vigas esbeltas de acero inoxidable.

ANTECEDENTES

En las últimas décadas se ha incrementado notablemente el estado del arte del comportamiento de vigas esbeltas de acero sometidas a carga concentrada, principalmente por la creciente popularidad del método de empujes sucesivos [5] para la puesta en sitio de puentes de acero. Lagerqvist [6] realiza estudios en vigas de acero de alta resistencia sometidas a carga concentrada y carga aplicada en el extremo sin rigidizar longitudinalmente (Figura 2). Finalmente propone un modelo para determinar la resistencia última de la viga que incluye tres partes: resistencia a fluencia del material, carga elástica de pandeo y una función de resistencia. Por consiguiente, Roberts y Newark [7] estudian la falla por pandeo localizado en el alma de vigas laminadas en caliente, obteniendo un modelo sencillo que muestra una gran correlación con datos experimentales, proponiéndolo para el diseño de vigas esbeltas sometidas a carga concentrada. Maiorana et al. [8] presentó una recopilación de diferentes modelos numéricos en la literatura para el pandeo de vigas esbeltas en puentes de acero por carga concentrada.

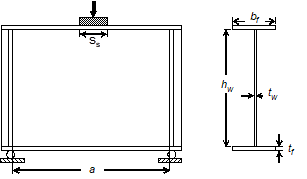
Figura 2. Geometría de una viga esbelta sometida carga concentrada.

El uso de acero inoxidable y otros materiales diferentes al acero estructural en vigas es poco reportado en la literatura. Mirambell y Real [9] estudiaron la influencia de la no linealidad del acero inoxidable en vigas sometidas a flexión en las deflexiones obtenidas experimentalmente con las obtenidas utilizando el Eurocódigo 3 Parte 1.4 [2].  Continuando, Real y Mirambell [10] proponen una formulación teórica para estimar las deflexiones en vigas de acero inoxidable, basada en la relación momento flector- curvatura de la viga y tomando en cuenta la no linealidad del material. Estudios sobre el comportamiento de vigas esbeltas de acero inoxidable sometidas a carga cortante son reportadas por Estrada et al. [11,12], Real et al. [13], y Armoosh et al. [14], entre otros. Oh et al. [13] investigaron mediante modelos numéricos y experimentales la resistencia última y diferentes modos de falla para vigas de aleaciones de aluminio bajo cargas concentradas. Los modelos no lineales utilizados presentaron una alta correlación con las pruebas experimentales.

Unosson [4] realizó estudios experimentales y numéricos de carga concentrada en vigas esbeltas de acero inoxidable, enfocándose en establecer diferencias entre las diferentes metodologías planteadas en la literatura para determinar la resistencia última de este tipo de vigas. Recientemente, Reis et al. [14] realizaron estudios numéricos para evaluar la resistencia de vigas a carga cortante sometidas a altas temperaturas, con el fin de poder predecir la resistencia última en situaciones de fuego. Sonu y Singh [15] desarrollaron modelos numéricos paramétricos para evaluar las características de vigas de acero inoxidable dúplex bajos tres modos de falla: cortante, flexión y combinado flexión-cortante, proponiendo modificaciones al EN 1993-1-4 (2006/A1:2015).

MODELADO POR ELEMENTOS FINITOS

En primer lugar, se elaboró un modelo numérico no lineal usando el método de los elementos finitos. Elementos tipo shell fueron utilizados para modelar el alma, ala de la viga y rigidizador transversal. Cuatro vigas ensayadas experimentalmente por Unosson [4] fueron utilizadas para validar el modelo por elementos finitos. Las dimensiones de las vigas se muestran en la Tabla 1 con sus correspondientes valores de carga última obtenida experimentalmente.

Debido a la simetría en la geometría, cargas y condiciones de borde, solo una mitad de cada viga fue modelada (Figura 3a). Para el mallado se utilizaron elementos shell cuadriláteros con 4 nodos y 6 grados de libertad por nodo. Un refinamiento en el mallado es realizado en la zona del alma inferior a la zona de aplicación de la carga.

Tal como se muestra en la Figura 3a, la carga fue aplicada mediante un nodo maestro vinculado a través de una restricción cinemática a todos los nodos ubicados en la región del ala superior a través de la longitud S_s /2. Además, en los nodos ubicados en esta región, tanto las rotaciones como los desplazamientos fuera del plano fueron restringidos. Las imperfecciones geométricas iniciales fueron modeladas como una función sinusoidal tanto en la dirección longitudinal como en la dirección transversal de la viga. La magnitud de la máxima amplitud de las imperfecciones iniciales (w_o) fue seleccionada de acuerdo a ENV 1993-1-5 [3].

En los apoyos se restringió únicamente el desplazamiento vertical en los nodos del ala inferior pertenecientes al extremo opuesto al plano de simetría. Posteriormente, se utiliza el método de Riks para trazar el comportamiento no lineal de las vigas cargadas.

Tabla 1. Dimensiones de vigas ensayadas experimentalmente por Unosson [4].

Viga	a [mm]	hw [mm]	tw [mm]	tf [mm]	bf [mm]	Ss [mm]	FR-EXP [kN]
Pli 4301-2	996	238.3	4.1	12.0	121.1	80	196
Pli 4301-3	1397	316.0	4.1	11.9	121.9	40	168
Pli 4301-4	1623	438.4	4.1	11.9	121.4	40	169
Pli 4301-5	1682	400.9	8.8	12.0	120.4	40	478

Las propiedades mecánicas del material fueron las mismas reportadas por Unosson [4], un acero inoxidable austenítico grado EN 1.4301 (AISI 304), considerándolo como un material isotrópico, despreciándose cualquier efecto producto de la anisotropía del material. La resistencia a fluencia de las aletas y del alma es f_yf =285 MPa y f_yw =297 MPa, respectivamente. Además, se consideró un módulo de Young E =200 GPa. El modelo del comportamiento no lineal del mismo se tomó de Rasmussen [16], pues esta correlación se ajusta notablemente al comportamiento no lineal del acero inoxidable, en concordancia con los lineamientos establecidos por ENV 1993-1-4 [2].

Figura 3. Modelo por elementos finitos (a) Malla empleada y modelo de carga; (b) Esfuerzos de von Mises [MPa] para la viga Pli 4301-3 para un desplazamiento de 10mm.

Validación

La carga fue aplicada mediante un desplazamiento controlado del nodo maestro y se utilizó el método de Riks para asegurar el trazado de la curva de equilibrio fuerza - desplazamiento ante la eventual presencia de pandeo en la viga. Luego de un análisis de convergencia el modelo final presenta una malla con 1056 elementos tipo shell. Los resultados parciales de esta validación se presentan en la Tabla 2, donde la resistencia a la flexión (M_R-ENV) es calculada según la metodología presentada en el ENV 1993-1-4 [4] y el momento máximo (M_max) se obtiene del diagram de moemnto de la viga.

Tabla 2. Comparación entre valores experimentales y los obtenidos por el método de los elementos finitos.

Viga	FR-EXP [kN]	FR-FEA [kN]	MR-ENV [kN.m]	Mmax [kN.m]
Pli 4301-2	196	202	106.3	48.9
Pli 4301-3	168	176	140.0	58.6
Pli 4301-4	169	182	192.6	68.5
Pli 4301-5	478	493	228.9	200.9

La correlación entre los datos experimentales y los resultados numéricos es satisfactoria. A pesar de la simplicidad del modelo numérico, el error en la resistencia última obtenida por el modelo numérico (F_R-FEA) no sobrepasa el 10% a los obtenidos experimentalmente. Adicionalmente, se observa una gran correlación entre las curvas fuerza – desplazamiento vertical obtenido numéricamente con las obtenidas experimentalmente (Figura 4). Para las simulaciones de las vigas Pli4301-2 y Pli4301-3 la rigidez inicial del modelo se ajusta a la rigidez de las vigas ensayadas, únicamente difieren en su valor de carga máxima y el comportamiento post crítico de los mismos sigue un patrón de carga similar a las curvas experimentales. A diferencia de estas, los modelo numéricos Pli4301-4 y Pli4301-5 presentan variaciones en la rigidez inicial, pero en líneas generales su patrón de carga de asemeja al obtenido en los experimentos, siendo estos los resultados

Figura 4. Comparación de curvas Fuerza -desplazamiento vertical entre modelo numérico y ensayos experimentales.

numéricos que presentan una mayor diferencia porcentual con los experimentos.  Las diferencias arrojadas por el modelo numérico y los ensayos se le pueden atribuir a la forma en que se aplica la carga a lo largo de S_s. En el modelo, la carga es aplicada directamente sobre los nodos con el objetivo de evitar condiciones de contacto y minimizar los tiempos computacionales.

Adicionalmente, otra fuente de discrepancia en los resultados podría ser la no inclusión de esfuerzos residuales en las vigas, originados por los procesos de soldadura en su fabricación, afectando esto al estado de esfuerzos de membrana originados en el alma, reduciendo la resistencia última de las vigas.

ANÁLISIS PARAMÉTRICO

Una vez validado el modelo se realizó un análisis paramétrico donde se estudia la influencia de la relación de espesores (t_f /t_w) y relación de zona de carga - ancho de viga (S_s /a) sobre la carga concentrada máxima. Para todo el análisis paramétrico la influencia de la flexión en mínima (M_max /M_R < 0.5).

Relación de zona de carga - largo de viga S_s /a.

A continuación se presenta el comportamiento de vigas esbeltas al variar la longitud de aplicación de la carga desde un valor mínimo de 0.1 hasta 0.3 veces el ancho de la viga. Para los resultados de las simulaciones presentados a continuación, se fijaron los siguientes valores: a = 800 mm, t_w= 4 mm, t_f /t_w = 2. En la Figura 5 se observa que al aumentar el área donde está aplicada la carga se aumenta la resistencia última de las vigas, independientemente de la relación de aspecto a/hw.   Al aumentar la longitud Ss se garantiza una transmisión de la carga sobre el alma en un área mayor, logrando que la distribución de esfuerzos de membrana no se concentre

Figura 5. Comparación de curvas fuerza - ddesplazamiento vertical variando S_s /a para dos relaciones de aspecto y longitud de viga constante.

Figura 6. Comparación de curvas Fuerza-Desplazamiento vertical variando la relación t_f /t_w para dos relaciones a/h.

en un área reducida y por ende se logre un aumento en la resistencia última. Para estas vigas, se obtuvo que la resistencia última según ENV 1993-1-5 [3] ocurre antes de que ocurra plastificación de las fibras del alma adyacentes a la región del ala donde está aplicada la carga.

Relación de espesores alma-ala de la viga t_f  / t_w.

Para el estudio preliminar de la influencia del parámetro t_f /t_w  se reportan los resultados manteniendo el espesor del alma de la viga fijo e igual a 4 mm y una longitud de aplicación de la carga igual a 10 mm. En la Figura 6 se observa que al aumentar el espesor del ala t_f proporcionalmente al espesor del alma de la viga t_w se obtiene un aumento en la resistencia última de la viga ante carga concentrada. Este comportamiento se debe a que al aumentar el espesor del ala, el momento plástico necesario para que se produzca la formación de rótulas plásticas en la misma aumenta, retardando la aparición de líneas de fluencia en el alma de la viga y que se produzca el pandeo localizado de la misma. Este mecanismo de colapso plástico en el alma de la viga es ampliamente reportado por Lagerqvist [5].

Otra manera de estudiar la influencia de t_f /t_w es observando la dependencia de la resistencia a flexión de la viga con este parámetro. En la Figura 7 se reporta la relación entre la carga máxima obtenida por el método de elementos finitos F_R-FEA y la carga F_R-ENV obtenida utilizando el procedimiento descrito en el ENV-1993-1-4 [2] , en función del cociente entre momentos últimos (M_R-FEA/M_R-ENV) obtenidos de la misma manera. En el ENV 1993-1-5 [3], el momento último de flexión se determina utilizando la teoría de los anchos efectivos para placas esbeltas sometidas a flexión, en la cual se considera que toda la zona sometida a tensión es completamente efectiva y solamente una porción de la zona sometida a compresión contribuye a la resistencia a flexión debido a la falla prematura causada por pandeo localizado.

A pesar de que en todos los resultados numéricos la relación M_R-FEA/M_R-ENV es menor a 0.5, y por ende no existe una influencia significativa entre estos parámetros, se observa como al aumentar la relación t_f /t_{w ,} el momento máximo que resiste la viga se aproxima cada vez más a la resistencia a la flexión estimada según [3], afectando con esto la carga concentrada máxima que puede soportar la viga. En consecuencia, al minimizar la relación t_f /t_w  la relación F_R-FEA / F_R-ENV se ve afectada, obteniéndose valores de carga máxima de diseño (F_R-ENV) mucho menores, logrando diseños estructurales con acero inoxidable para este tipo de aplicación menos eficientes debido a la necesidad de utilizar una mayor cantidad de material.

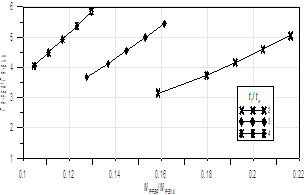
Figura 7. Relación de resistencias últimas en función de la relación entre resistencias a la flexión para 3 valores de t_f /t_w

ESTUDIO DE LA CARGA ÚLTIMA OBTENIDA NUMÉRICAMENTE CON PROCEDIMIENTO PRESENTADO EN ENV-1993-1-5 [4].

En la Figura 8 se reporta la distribución de la relación F_R-FEA / F_R-ENV obtenida del análisis paramétrico en función de la relación de esbeltez de la vigas λ, siendo ésta una relación proporcional al cociente entre la carga de fluencia y la carga de pandeo elástico del alma [5], indicando con esto que al ser superior a 1, se garantiza una falla por pandeo localizado antes de que ocurra endurecimiento por deformación plástica de las fibras del material. A pesar de que los resultados mostrados en la Figura 8 se encuentran agrupados en función de la longitud relativa de aplicación de la carga, no se observa un patrón que determine cuando los valores de diseño son considerablemente menores respecto a los obtenidos numéricamente, por lo que para vigas geométricamente similares este factor de seguridad en el diseño por ENV-1993-1-4 [2] no varía linealmente con la relación S_s /a.

La diferencia entre la carga máxima numérica y la obtenida por ENV-1993-1-4 [2] se hace mayor a medida que la relación de esbeltez aumenta, pues existen situaciones en los que esta relación es de 8:1, haciendo entonces que la carga máxima obtenida con [2] para una viga de acero inoxidable podría ser 8 veces menor a la carga que la estructura podría soportar, de acuerdo a los resultados obtenidos numéricamente. Solo para relaciones de esbeltez bajas y siguiendo la metodología de diseño de estructuras de acero inoxidable [2] se podrían obtener diseños de vigas esbeltas de acero mucho más realistas, logrando diseños menos robustos y por ende una disminución en los costos en la adquisición de material.

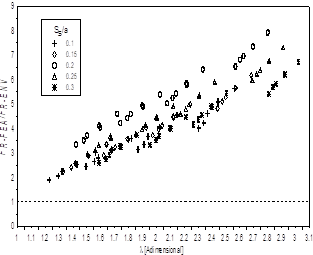
Figura 8. Relación F_R-FEA/F_R-ENV en función de la relación de esbeltez λ.

CONCLUSIONES

El uso de acero inoxidable en sustitución de aceros al carbono con fines estructurales es una opción tentadora pues este presenta ventajas con relación a sus propiedades mecánicas, resistencia a la corrosión, resistencia al fuego y una menor inversión por costos de mantenimiento.

El modelo no lineal por elementos finitos propuesto representa adecuadamente el comportamiento estructural de vigas esbeltas de acero inoxidable sometidos a carga concentrada, obteniendose variaciones en la resistencia última no mayores al 10% respecto a valores obtenidos experimentalmente.

A pesar de que se reportaran los resultados preliminares en el análisis paramétrico, se observa que las variables S_s /a y t_f / t_w  influyen notablemente en la resistencia última de vigas esbeltas.

Los valores de resistencia última de diseño obtenidos empleando el Eurocódigo 3 Parte 1.4 [2] son mucho menores respecto a los obtenidos en las simulaciones numéricas. Esto se debe a que en el Eurocódigo la metodología planteada se basa en el diseño de estructuras utilizando aceros al carbono, por lo que no se aprovecha del todo las ventajas del comportamiento estructural de aceros inoxidables. Como consecuencia, se obtienen diseños muy robustos al no aprovechar eficientemente el uso del material, logrando con esto un aumento significativo de los costos.

UNIDADES Y NOMENCLATURA

a      longitud de la viga (mm)

b_f ancho del ala de la viga (mm)

F_R-ENV carga concentrada máxima según Eurocódigo 3 Parte 1.4 (kN)

F_R-EXP carga concentrada máxima obtenida experimentalmente (kN)

F_R-FEA carga concentrada máxima obtenida numéricamente (kN)

h_w       altura de la viga (mm)

M_max momento flector máximo obtenido con la resistencia última  (kN m)

M_R momento flector máximo (kN m)

M_R-ENV momento flector máximo calculado según Eurocódigo 3 Parte 1.4 (kN m)

S_s     longitud de aplicación de la carga (mm)

t_f      espesor del ala de la viga(mm)

t_w     espesor del alma de la viga (mm)

λ      relación de esbeltez (adimensional)

REFERENCIAS

[1] G. Abbruzzese y M. Barteri, Structural Applications of Stainless Steel, Proceedings of the 1st International Conference Super-High Strength Steel, Rome, Italy, Nov. 2005.

[2] ENV 1993-1-4:1996 Eurocode 3 - Design of steel structures – Part 1.4: General rules – Supplementary rules for stainless steels, 2005.

[3] ENV 1993-1-5:2004 Eurocode 3 – Design of steel structures – Part 1.5: General rules – Supplementary rules for planar plated structures without transverse loading, 2004.

[4] E. Unosson, Patch Loading of Stainless Steel Girders: Experiments and Finite Element Analyses, Licentiate Thesis, Lulea University of Technology, Department of Civil and Mining Engineering, Division of Steel Structures, Lulea, Sweden, 2003.

[5] R. Valle Pascual, N. F. Carvajal Monsalve, J. C. Botero Palacio. Evolución de los parámetros geométricos de diseño en puentes construidos con voladizos sucesivos in situ, UIS Ingenierías, vol. 16(1), 86-96, Ene-Jun. 2017.

[6] O. Lagerqvist, Patch loading- Resistance of Steel Girders Subjected to Concentrated Forces, Ph.D. Thesis, Lulea University of Technology, Department of Civil and Mining Engineering, Division of Steel Structures, Lulea, Sweden, 1994.

[7] T. M. Roberts y A. C. B. Newark, Strength of Webs Subjected to Compressive Edge Loading, Journal of Structural Engineering, vol. 123(2), pp. 176-183, Feb. 1997.

[8] E. Maiorana, A. Miazzon y L. Briseghella, Web Buckling, Patch Loading and Launching Bridges, Proceedings of I International Conference Super-High Strength Steel, Rome, Italy, Nov. 2005.

[9] E. Mirambell and E. Real, On the Calculation of Deflections in Structural Stainless Steel Beams: An Experimental and Numerical Investigation, Journal of Constructional Steel Research, vol. 54(1), pp. 109–133, Apr.  2000.

[10] E. Real and E. Mirambell, Flexural Behaviour of Stainless Steel Beams, Engineering Structures, vol. 27(10), pp. 1465–1475, 2005.

[11] I. Estrada, E. Real y E. Mirambell, General Behaviour and Effect of Rigid and Non-Rigid End Post in Stainless Steel Plate Girders Loaded in Shear. Part I: Experimental Study, Journal of Constructional Steel Research, vol. 63(7), pp. 970-984, Jul. 2006.

[12] I. Estrada, E. Real y E. Mirambell, General Behaviour and Effect of Rigid and Non-Rigid End Post in Stainless Steel Plate Girders Loaded in Shear. Part II: Extended Numerical Study and Design Proposal, Journal of Constructional Steel Research, vol. 63(7), pp. 985-996, 2006.

13] E. Real, E. Mirambell y I. Estrada, Shear Response of Stainless Steel Plate Girders, Engineering Structures, vol. 29(7), pp. 1626-1640, 2007.

[14] S. R. Armoosh, A. R. Khalim y A. S. Mahmood, Shear response of lean duplex stainless steel plate girders, Structural Engineering and Mechanics, vol. 54(6), pp. 1267-1281, 2015.

[15] Y. C. Oh, D. G. Bae, J. Y. Ko, Basic Research for Resistance Prediction of Aluminium Alloy Plate Girders Subjected to Patch Loading, Journal of the Korean Society of Marine Environment & Safety, vol. 20(2), pp. 218-27, 2014.

[16] A. Reis, N. Lopes, P. Vila Real. Numerical study of steel plate girders under shear loading at elevated temperatures, Journal of Constructional Steel Research, 117, pp. 1-12, 2016.

[17] J. K. Sonu, K. D. Singh. Shear characteristics of Lean Duplex Stainless Steel (LDSS) rectangular hollow beams, Structures, vol. 10, pp. 13-29, 2017.

[18] K. J. R. Rasmussen, Full Range Stress-Strain Curves for Stainless Steel Alloys, Journal of Constructional Steel Research; vol. 59(1), pp. 47-61, 2003.