Algoritmos de optimización en la estimación de propiedades termodinámicas en tiempo real durante el tratamiento térmico de materiales con microondas

 

Optimization algorithms applied in the real-time thermodynamics properties estimation during a material thermal treatment with microwaves

 

 

 

Edgar García¹, Iván Amaya ², Rodrigo Correa³

 

 

¹Grupo de Investigación en Control, Electrónica, Modelado y Simulación - CEMOS, Escuela de Ingeniería Eléctrica, Electrónica y Telecomunicaciones - E3T, Universidad Industrial de Santander, Colombia. Email: edgar.garcia1@correo.uis.edu.co

2Escuela de Ingeniería y Ciencias,  Instituto Tecnológico de Monterrey, México. Email: iamaya@itesm.mx

3 Grupo de Investigación en Control, Electrónica, Modelado y Simulación - CEMOS, Escuela de Ingeniería Eléctrica, Electrónica y Telecomunicaciones E3T, Universidad Industrial de Santander, Colombia. Email: crcorrea@uis.edu.co

 

 

 

RESUMEN

 

Este trabajo considera la predicción en tiempo real de parámetros térmicos de una muestra sometida a radiación. Se estimaron la conductividad térmica y la capacidad calorífica. Se modeló el flujo volumétrico interno de calor uniforme y constante en el tiempo. Para resolver el problema inverso se usaron algoritmos de optimización global tales como el método de la espiral, el método de búsqueda en vórtice, el método de pesos ponderados, el método de enjambre de partículas unificado, el método de optimización del campo electromagnético y el método de búsqueda armónica de ancho auto-regulado. Los resultados muestran que todos los algoritmos empleados estiman correctamente estos dos parámetros siempre y cuando, la relación señal a ruido (SNR) de las muestras (simuladas en este trabajo) esté por encima de 30 [dB]. Por ende, para propósitos prácticos, si se dispone de un buen diseño experimental y una buena instrumentación, se podrían estimar con alta precisión estos parámetros en tiempo real.

 

PALABRAS CLAVE: Calentamiento por microondas, Estimación de parámetros, Métodos de optimización global, Problema inverso.

 

 

ABSTRACT

 

This work considers the real-time prediction of thermal parameters for a cylindrical sample heated in a uniform electromagnetic field. The thermal conductivity () and the heat capacity () were estimated for the present case. The inner volumetric electromagnetic flux radiation process was modeled as uniform and constant in time. The spiral optimization algorithm (SOA), the vortex search (VS), the weighted attraction method (WAM), the unified particle swarm optimization (UPSO), the electromagnetic field optimization (EFO) and the self-regulated fret-width harmony search algorithm (SFHS) were used to solve the ill-posed inverse problem. Results showed that all employed algorithms correctly estimated these two parameter only if the signal-to-noise-ratio of the measured samples (simulated in this work) were above of 30 [dB]. Therefore, for practical purposes, these parameters can be estimated in real-time if a good experimental design and a correctly specified electronic instrumentation are available.

 

KEYWORDS: Parameter estimation, Microwave heating, Global optimization methods, Inverse problem.

 

INTRODUCCIÓN

 

En muchos problemas de la ingeniería tales como la mecánica, la química, la electrónica o la aeroespacial, es de gran importancia la estimación de parámetros termodinámicos. Sin embargo, en algunos casos los métodos convencionales de estimación no proveen resultados satisfactorios ya que la industria moderna cada vez es más sofisticada. Lo que requiere que dichas estimaciones sean más precisas y en tiempo real [1]. Complementariamente, el calentamiento con microondas es un campo que desde su descubrimiento ha ido aumentando su popularidad [2], dentro de las ventajas potenciales de este calentamiento sobre los métodos convencionales se encuentran el reducido tiempo de procesado térmico del material y el calentamiento volumétrico, lo que permite que este sea uniforme dentro del sólido [3]. Ante estas ventajas, algunos investigadores han propuesto hacer uso de las microondas para la estimación de parámetros tales como las propiedades electromagnéticas del material [4], [5].

 

Por otra parte, un problema inverso puede verse como un procedimiento para estimar, a partir de una serie de observaciones, las principales causas que lo producen [6]. Una breve revisión de la literatura acerca de los problemas inversos para la estimación de parámetros muestra que en el trabajo de Dasa [7] se predijo la conductividad térmica y el coeficiente de temperatura superficial de una aleta hiperbólica haciendo uso de un algoritmo de optimización. Adicionalmente, Adamsyk [8] describió una técnica experimental combinada con la solución de un problema inverso para la estimación de la conductividad térmica de materiales isótropos y ortótropos haciendo uso de métodos clásicos de optimización tales como Levenberg-Mardquardt. Por otro lado, Huntul [9] realizó problemas inversos para la reconstrucción de la conductividad térmica dependiente del tiempo. Para ellos, usó los métodos de regularización de Tikhonov.

 

Finalmente, Mohebbi [10] propuso una metodología para estimar parámetros tales como la conductividad térmica, el coeficiente de transferencia de calor y el flujo de calor de cuerpos con geometría irregulares haciendo uso de algoritmos de optimización basados en el gradiente.

 

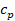En vista de lo anterior, este trabajo considera un enfoque de problema inverso para la estimación de propiedades térmicas tales como la conductividad  y la capacidad calorífica  de un material, de geometría cilíndrica, que es sometido a radiación electromagnética y cuyo perfil de temperatura es conocido de antemano. Se asumieron que estas temperaturas fueron tomadas de múltiples sensores (i.e., 3) en posiciones dentro del sólido.

 

Adicionalmente, para solucionar el problema inverso, se usaron técnicas de optimización moderna tales como los metaheuristicos. Esto es debido, principalmente, a su popularidad para solucionar de manera eficiente problemas de elevada complejidad [11]–[13].

 

En este manuscrito se incluye una sección con una breve descripción de los algoritmos usados para la solución del problema inverso, a la vez que se declaran el problema directo e inverso, para finalizar con la solución del problema directo, así como con la forma en la que definimos el registro de temperaturas y la función objetivo (Sección 2). La Sección 3, por su parte, presenta los resultados más relevantes y su análisis. Finalmente, la Sección 4 incluyen las conclusiones más importantes de este trabajo.

 

MÉTODOS

 

En esta sección se muestra una breve descripción de los métodos metaheurísticos usados en este trabajo. La principal razón detrás de esta decisión fue probar distintas estrategias de optimización global modernas para solucionar este problema. Luego, se declaran los problemas directo e inverso y una vez realizado esto, se incluye la solución del problema directo y un análisis de cómo se obtuvieron las mediciones de temperatura. Finalmente, esta sección concluye con la definición de la función objetivo a resolver.

 

1.1. Fundamentos de los algoritmos

 

A continuación, se da una breve explicación de los algoritmos metaheurísticos usados en este trabajo:

 

1.1.1. Método de la espiral.

El algoritmo de la espiral (SOA) se basa en el comportamiento en espiral presente en la naturaleza tales como los frentes de presión y la vía láctea [14]. El algoritmo básico consta de cinco pasos, que se presentan en la Tabla 1.

 

1.1.              

1.1.1.                 

1.1.2.  

1.1.1.  

1.1.2. Método de la búsqueda en vórtice.

El algoritmo de búsqueda en vórtice (VS) se basa en el comportamiento del flujo vertical de un fluido que se encuentra agitado [15]. El algoritmo básico consta de cuatro pasos, resumidos en la Tabla 2.

 

 

 

 

 

 

1.1.3. Método de la atracción ponderada.

El algoritmo de la atracción ponderada (WAM) se basa en el comportamiento de atracción gravitacional entre las

partículas [16]. El algoritmo básico consta de cinco pasos, que se presentan en la

Tabla 3.

 

 

Tabla 1. Pseudocódigo del método de la espiral.

Fuente. Elaboración propia.

 

 

Tabla 2. Pseudocódigo del método de la búsqueda en vórtice.

Fuente. Elaboración propia.

 

1.1.4. Método del enjambre de partículas unificado.

Este algoritmo^[1] (UPSO) reúne dos variantes principales del PSO original [17] en un esquema unificado que combina las mejores características en cuanto a la exploración y la explotación dentro del espacio de búsqueda [18]. La Tabla 4 muestra los cinco pasos del algoritmo básico.

 

 

1.1.5. Método de optimización del campo electromagnético.

 El algoritmo^[2] de la optimización del campo electromagnético (EFO) está inspirado en el comportamiento de los electroimanes con diferentes polaridades y toma ventaja del radio inspirado en la naturaleza conocido como el radio de oro [19]. El algoritmo básico consta de seis pasos, como muestra la Tabla 5.

1.1.6. Método de la búsqueda armónica de ancho auto-regulado.

Este algoritmo (SFHS) fue planteado originalmente por Geem et al. [20] y modificado por Amaya et al. [21]. Este algoritmo se basa en el proceso en el que los músicos buscan nuevas armonías para sus composiciones. La Tabla 6 muestra los siete pasos del algoritmo.

 

Tabla 3. Pseudocódigo del método de la atracción ponderada.

Fuente. Elaboración propia.

Tabla 4. Pseudocódigo del método del enjambre de partículas unificado.

Fuente. Elaboración propia.

 

 

Tabla 5. Pseudocódigo del método de optimización del campo electromagnético.

Fuente. Elaboración propia.

 

 

1.2. Modelo del sistema

 

En este trabajo consideramos un sólido de forma cilíndrica homogéneo e isotrópico de radio  con densidad constante  y calor específico . La ecuación de calor expresada en coordenadas cilíndricas, asumiendo ninguna variación en los ejes (, ) y que la tasa de generación interna por unidad de volumen en el punto  es constante de magnitud , se muestra en la ecuación (1), donde  es la difusividad térmica del material,  es la conductividad térmica del material y  es el flujo de calor generado en el sólido en el punto . Además,  es el perfil de temperatura y la relación que existe entre  y  esta dada por . Las temperaturas en sus fronteras y las condiciones iniciales se asumieron cero.

 

 

 

 

1.2.1. Declaración del problema directo.

Es posible describir la distribución de la temperatura dentro de un cilindro calentado homogéneamente con microondas. Aquí, se asumen que todos los parámetros del modelo matemático son conocidos, incluyendo las condiciones iniciales y las condiciones de fronteras.

 

1.2.2. Declaración del problema inverso.

Se puede estimar los parámetros tales como la conductividad térmica  y la capacidad calorífica  del material escogido como ejemplo (i.e., SiC). Para ello se requiere de mediciones de temperatura tomadas con uno o múltiples sensores (i.e., 3) localizados en posiciones exactas dentro del sólido.

Tabla 6. Pseudocódigo del método de búsqueda armónica de ancho auto-regulado.

Fuente. Elaboración propia.

 

1.3. Solución del problema directo

 

Este problema dispone de una solución analítica en [22] que conduce al perfil de temperatura mostrado en la ecuación (2).

 

 

En la Figura 1 se observa el perfil de temperatura para el caso en el que el sólido calentado es una muestra de Carburo de Silicio (SiC) [23]. En la Tabla 7 se detallan los parámetros de simulación.

 

1.4. Mediciones de temperatura

 

Debido al enfoque de simulación considerado para este trabajo, construimos mapas de temperatura sintéticos para simular las mediciones de temperatura que se darían en un escenario real.

 

Tabla 7. Parámetros usados para la solución del problema directo.

Fuente. Elaboración propia.

 

Figura 1. Perfil de temperatura en función del radio y del tiempo para un cilindro con generación interna constante de magnitud . Los números sobre las curvas representan el tiempo en segundos [s]. Fuente. Elaboración propia.

 

Para crear estas temperaturas sintéticas añadimos ruido blanco Gaussiano (WGN) a los valores teóricos de temperatura. Por tanto, asumimos como válidas las condiciones estadísticas expresadas por Beck [24], entre las que destacan: errores aditivos, no correlacionados y de distribución normal con media cero y desviación estándar constante.

 

Es importante resaltar que la temperatura es una variable continua, pero que, al tomar mediciones con un sensor, esta señal se discretiza. Para construir las mediciones sintéticas se empieza midiendo la potencia de la señal , como se muestra en la ecuación (3). Luego, se calcula el vector de ruido aleatorio  como se muestra en la ecuación (4), donde el  es la tasa de señal a ruido en [dB] y  es un vector de números aleatorios con distribución normal. Finalmente, la temperatura medida  se obtiene sumando los vectores de la temperatura teórica  y el ruido  como se observa en la ecuación (5). A modo de brevedad los vectores  y  se renombraron como  y  en el texto.

 

 

 

 

Por otra parte, en la Figura 2 se observa un ejemplo de las temperaturas medidas , con un sensor, en 0 [cm] para diferentes tiempos entre 0 y 30 [s] en comparación con la temperatura teórica . Los sensores se simularon con dos niveles de  (i.e., 10 y 30 [dB]) para observar el efecto que tendrá el nivel de ruido en la señal reconstruida. Por motivos de espacio no se incluyen las gráficas para los otros dos sensores ubicados en  2.5 y 5 [cm]

Figura 2. Ejemplo de temperaturas medidas (sintéticas) con un sensor en el intervalo entre t=0 a 30 [s] para un SNR de 10 y 30 [dB] en comparación con la temperatura teórica. Fuente. Elaboración propia.

 

1.5. Función objetivo

 

La función objetivo es la norma cuadrada la cual se muestra en la ecuación (6), donde  son las temperaturas medidas, y  es la temperatura estimada por el modelo de la ecuación (2).

 

 

 

 

 

 

RESULTADOS

 

En esta sección, primero se muestran los parámetros usados en los algoritmos de optimización, luego se estiman los parámetros termodinámicos y por último realiza un análisis del rendimiento de los algoritmos. Los siguientes resultados se obtuvieron en un computador Intel Core i5 con sistema operativo Windows 7 de 64 bits y 6 [GB] de RAM.

 

1.6. Parámetros de los algoritmos de optimización

 

Los parámetros usados en los algoritmos de optimización se muestran en la Tabla 8. Estos parámetros fueron escogidos debido a que presentaron buenos resultados en pruebas preliminares sobre la función objetivo que por motivos de espacio no fueron incluidas en este documento.

Tabla 8. Parámetros usados en los algoritmos de optimización, seleccionados con base en pruebas preliminares (omitidos por motivos de espacio). Nota: Los pararámetros  se escriben en notación científica para reducir espacios en la tabla.

Fuente. Elaboración propia.

1.7. Determinación de los parámetros 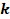 y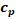

 

Para la determinación de los parámetros  y 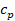 se usaron los algoritmos metaheurísticos anteriormente descritos. Estos se ejecutaron 100 veces y los resultados obtenidos tales como el promedio, desviación estándar, mejor resultado, peor resultado y el error RMS de la señal reconstruida en relación con la señal original se sintetizaron en la Tabla 9. De esta tabla se puede resaltar que un valor bajo de SNR (i.e., 10 [dB]) conduce a un error en la estimación de los parámetros  y 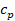 cercano al 6 y 15%, pues debían ser 90 y 920, respectivamente (Tabla 7). Sin embargo, al aumentar el SNR a 30 [dB] se puede observar que el margen de error se reduce a 0.4 y 0.1 %, respectivamente. Por otro lado, se puede concluir que todos los algoritmos convergieron a sus valores esperados debido a que sus errores RMS fueron cercanos a cero. Finalmente se puede observar que WAM fue el algoritmo que tuvo menos variabilidad en sus respuestas y que por el contrario EFO y UPSO fueron los que tuvieron la mayor.

 

1.8. Análisis del rendimiento y precisión de los algoritmos

 

En esta sección se lleva a cabo un análisis del rendimiento de los algoritmos usados en este trabajo, para ello se revisó el número de iteraciones que empleó cada algoritmo, al igual que el número de veces que se evaluó la función objetivo y se les calculó un parámetro asociado a la precisión haciendo uso de la ecuación (8). Estos resultados se sintetizaron en la Tabla 10. Es importante tener en cuenta que se consideró como acierto aquellos valores de  y 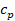 que se encontraban dentro de un intervalo de confianza del 5% con respecto al valor esperado. De esta tabla se puede observar que el algoritmo de VS fue el más eficiente en comparación con los otros algoritmos en cuanto al uso de iteraciones y evaluaciones de la función objetivo. Por otra parte, se observa que la precisión de los algoritmos para un SNR de 10 [dB] es de cero. Esto se debe a que este nivel de ruido representa una señal en donde éste es tan severo, que resulta imposible descifrar la medición correcta. Sin embargo, para un nivel de SNR de 30 [dB] la precisión fue superior al 97%.

 

(8)

 

 

 

 

 

CONCLUSIONES

 

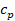En este artículo se analizaron técnicas alternativas para la estimación, en tiempo real, de la conductividad térmica  y de la capacidad calorífica  de un material sometido a las microondas. Se encontró que todos los algoritmos de optimización seleccionados se pueden usar para este propósito siempre y cuando el nivel de ruido presente en las mediciones sea mínimo (SNR>30 [dB]). Esto significa que la estimación es altamente dependiente de la calidad del montaje experimental de medición y de la instrumentación electrónica usada. Si estos dos requerimientos se satisfacen, es posible estimar los parámetros en tiempo real sin la necesidad de montajes adicionales. Por otra parte, en el caso de los algoritmos de optimización se observó que todos convergieron a los valores esperados según el nivel de ruido presente en las mediciones. Sin embargo, al detallar el rendimiento de cada uno de ellos se puede observar que el algoritmo de VS aventaja considerablemente a los demás algoritmos en cuanto a iteraciones y evaluaciones de la función objetivo. Esto significa que emplea menos tiempo de cómputo con respecto a los demás. Finalmente, se puede observar que EFO y SFHS son los algoritmos con menor rendimiento debido a que emplean casi 5 y 377 veces más iteraciones y cerca de 8 y 377 veces más evaluaciones de la función objetivo, respectivamente, que el mejor encontrado. Adicionalmente, UPSO, SOA y WAM emplearon iteraciones similares a las de VS, sin embargo, cada uno de ellos emplearon cerca de 6, 3 y 3 veces, más evaluaciones de la función objetivo, respectivamente, con respecto al mejor encontrado. Lo que los convierte aparentemente en estrategias inviables ya que en esta aplicación en particular se necesitan principalmente estrategias que reduzcan el costo computacional y con alto grado de precisión.

 

Algunos trabajos futuros que pueden derivarse de esta investigación incluyen el análisis de diferentes materiales (con diferentes comportamientos), así como la inclusión de diferentes geometrías y de diferentes características para la fuente de irradiación. Todo esto con el fin de cubrir más escenarios y poder detectar condiciones en las que cada uno de los algoritmos utilizados en este trabajo se desempeñe adecuadamente.

 

AGRADECIMIENTOS

 

Los autores expresan su gratitud por el apoyo financiero brindado por la Universidad Industrial de Santander.

 

Tabla 10. Parámetros de rendimiento y eficiencia de los algoritmos tales como las iteraciones y evaluaciones de la función objetivo promedio junto con su desviación estándar. Así como la precisión (Prec.) obtenida de las 100 ejecuciones de cada algoritmo.

Fuente. Elaboración propia.

 

REFERENCIAS

 

[1] Necati Ozisik, “Introduction and concepts,” in Heat transfer - abasic approach, Internatio., A. Murphy and M. Eichberg, Eds. Singapore: McGraw-Hill Book Co, 1985, pp. 1–18.

 

[2] J. Osepchuk, “A History of Microwave Heating Applications,” IEEE Trans. Microw. Theory Tech., vol. 32, no. 9, pp. 1200–1224, 1984.

 

[3] National Research Council, “Microwave applications,” in Microwave Processing of Materials, Washington, DC: The National Academies Press., 1994.

 

[4] J. M. Catalá-Civera, A. J. Canós, P. Plaza-González, J. D. Gutiérrez, B. García-Baños, and F. L. Peñaranda-Foix, “Dynamic Measurement of Dielectric Properties of Materials at High Temperature During Microwave Heating in a Dual Mode Cylindrical Cavity,” IEEE Trans. Microw. Theory Tech., vol. 63, no. 9, pp. 2905–2915, 2015.

 

[5] L.-F. Chen, C. K. Ong, C. P. Neo, and V. V. Varadan, Microwave Electronics, Measurement and Materials Characterization, 1st ed. Wiltshire, Great Britain: John Wiley & Sons, 2004.

 

[6] M. J. Colaço, H. R. B. Orlande, and G. S. Dulikravich, “Inverse and optimization problems in heat transfer,” J. Brazilian Soc. Mech. Sci. Eng., vol. 28, no. 1, pp. 1–24, 2006.

 

[7] R. Dasa, “Identification of materials in a hyperbolic annular fin for a given temperature requirement,” Inverse Probl. Sci. Eng., vol. 24, no. 2, pp. 213–233, 2016.

 

[8] W. P. Adamczyk, R. A. Białecki, and T. Kruczek, “Retrieving thermal conductivities of isotropic and orthotropic materials,” Appl. Math. Model., vol. 40, pp. 3410–3421, 2015.

 

[9] M. J. Huntul, D. Lesnic, and M. S. Hussein, “Reconstruction of time-dependent coefficients from heat moments,” Appl. Math. Comput., vol. 301, pp. 233–253, 2017.

 

[10] F. Mohebbi and M. Sellier, “Estimation of thermal conductivity, heat transfer coefficient, and heat flux using a three dimensional inverse analysis,” Int. J. Therm. Sci., vol. 99, pp. 258–270, 2016.

 

[11] E.-G. Talbi, “Common Concepts for Metaheuristics,” in Metaheuristics, from Design to Implementation, 1st ed., New Jerey: John Wiley & Sons, 2009, pp. 1–79.

 

[12] H. G. Sánchez, J. Uscátegui, and S. Gómez, “Metodología para la detección de fallas en una estructura entramada metálica empleando las técnicasde análisis modal y PSO,” UIS Ing., vol. 16, no. 2, Jul - Dic, 2017, pp. 43–50.

 

[13] F. A. Zúñiga-Cortés, E. . Caicedo-Bravo, and D. . López-Santiago, “Gestión óptima de la potencia eléctrica en una microrred conectada, basada en el algoritmo genético para optimización multiobjetivo MOGA,” UIS Ing., vol. 15, no. 2, Jul- Dic, 2016, pp. 17–33.

 

[14] K. Tamura and K. Yasuda, “Spiral Multipoint Search for Global Optimization,” in 2011 10th International Conference on Machine Learning and Applications and Workshops, 2011, pp. 470–475.

 

[15] B. Dogan and T. Olmez, “A new metaheuristic for numerical function optimization: Vortex Search algorithm,” Inf. Sci. (Ny)., vol. 293, pp. 125–145, 2015.

 

[16] G. Friedl and M. Kuczmann, “A New Metaheuristic Optimization Algorithm, the Weighted Attraction Method,” Acta Tech. Jaurinensis, vol. 8, no. 3, pp. 257–266, 2015.

 

[17] J. Kennedy and R. Eberhart, “Particle swarm optimization,” 1995 IEEE Int. Conf. Neural Networks (ICNN 95), vol. 4, pp. 1942–1948, 1995.

 

[18] K. E. Parsopoulos and M. N. Vrahatis, “UPSO: A unified particle swarm optimization scheme,” Lect. Ser. Comput. Comput. Sci., vol. 1, pp. 868–873, 2004.

 

[19] H. Abedinpourshotorban, S. Mariyam Shamsuddin, Z. Beheshti, and D. N. A. Jawawi, “Electromagnetic field optimization: A physics-inspired metaheuristic optimization algorithm,” Swarm Evol. Comput., vol. 26, pp. 8–22, 2016.

 

[20] Z. Geem, J. Kim, and G. V Loganathan, “A New Heuristic Optimization Algorithm: Harmony Search,” Simulation, vol. 76, no. 2, pp. 60–68, 2001.

 

[21] I. Amaya, J. Cruz, and R. Correa, “Harmony Search algorithm: a variant with Self-regulated Fretwidth,” Appl. Math. Comput., vol. 266, pp. 1127–1152, 2015.

 

[22] H. S. Carslaw and J. C. Jaeger, “The flow of heat in a infinite circular cylinder,” in Conduction of heat in solids, 2nd ed., Oxford University Press, 1959, pp. 187–213.

 

[23] Grup d’Innovació per la Millora de la Docència en Estructura Propietats i Processat de Materials, “Materials - Silicom Carbide.” [Online]. Available: http://www.ub.edu/cmematerials/es/content/carburo-de-silicio-sic. [Accessed: 16-Jun-2016].

 

[24] J. Vere Beck and A. Kenneth, “Introduction To Linear Estimation,” in Parameter Estimation in Engineering and Science, New York: John Wiley & Sons, 1977, pp. 130–212.