7

INTRODUCCIÓN

Un dispositivo de absorción de energía es un sistema que convierte, total o parcialmente la energía cinética en otra forma de energía [1]. A fin de alcanzar una respuesta deseable de estos dispositivos, es recomendable que además de seleccionar una configuración adecuada, se admitan una variedad de criterios importantes para escoger los materiales y elementos a incorporar cuyas propiedades permitan obtener a un costo relativamente bajo, un mejor desempeño de éstos en términos de carga y eficiencia estructural. De allí que, en muchas aplicaciones de ingeniería, se requiera la consideración integral de criterios y parámetros cualitativos y cuantitativos, así como de experiencias prácticas y técnicas que permitan a los diseñadores e ingenieros llegar a un consenso sobre el diseño y selección de materiales para una aplicación específica. No obstante, esto puede llegar a ser una ardua labor cuando los criterios son expresados en unidades diferentes o datos difíciles de cuantificar.

Alghamdi [2] y Olabi et al. [3] resumieron numerosas investigaciones llevadas a cabo para caracterizar la capacidad de absorción de energía de tubos circulares y otras configuraciones fabricadas en diferentes materiales y aleaciones. En los últimos años la necesidad de producir estructuras simples, ligeras y altamente resistentes, aunado al incremento en las restricciones de costos, ha dado un obligatorio impulso en las compañías de tecnología automotriz, aeronáutica, ferroviaria y construcción, para ensayar nuevos materiales que satisfagan tales requerimientos. El metal expandido es uno de los materiales que más destaca por su aplicabilidad, versatilidad, características ecológicas, capacidad de producción en distintos formatos y excelentes propiedades mecánicas.

En la literatura concerniente, algunos autores se han abocado a investigar numérica y experimentalmente los distintos usos de este material en aplicaciones estructurales, con el fin de obtener modelos de comportamiento bajo diferentes tipos de cargas [1,4-7]. Sin embargo, muchas investigaciones se han concentrado típicamente en evaluar limitados criterios de respuesta en lugar de considerar un razonamiento multi-respuesta para descomponer el análisis de estos dispositivos en un conjunto de atributos que permitan una elección óptima y satisfactoria entre un conjunto de alternativas. Por esta razón, los métodos de análisis multi-criterio constituyen una inestimable herramienta en estos procesos de toma de decisiones para integrar la información técnica, cuantitativa y cualitativa de los elementos involucrados [8]. Experiencias satisfactorias con métodos de análisis multi-criterio se han encontrado en la solución de problemas de diseño en muchos campos como: construcción [9], gerencia de proyectos [10], absorción de energía [11], diseño conceptual de sistemas mecánicos y procesos de selección de materiales [12-15], optimización paramétrica [16] y en otros problemas de ingeniería [17].

En este artículo se ha desarrollado un análisis multi-criterio por los métodos AHP (AHP - Analytic Hierarchy Process) y COPRAS (Complex Proportional Assessment) para evaluar diferentes parámetros de carga y resistencia al impacto que permitan una selección numérica de la mejor opción entre seis configuraciones de tubos circulares fabricados con láminas de metal expandido y láminas sólidas. La capacidad de carga fue evaluada a partir de dos niveles: 1) la carga máxima P_máx [1]; y 2) la carga media P_m [18]; mientras que las características de resistencia al impacto analizadas fueron: eficiencia estructural η_e [19], energía total absorbida E_a [1], energía específica E_s [20], energía absorbida por unidad de longitud inicial E_Li [20], energía absorbida por unidad de longitud comprimida E_Lc[21], eficiencia de compactación η_c [22], eficiencia de energía η_E [23], longitud de compactación por unidad de masa L_cm [24] y eficiencia total η_t [22].

TÉCNICAS EXPERIMENTALES

Condiciones de ensayo y propiedades de los materiales

Un total de seis configuraciones circulares fueron sometidas a compresión axial cuasi-estática en una máquina de ensayo universal Page Wilson Measurement System modelo 60HD a una velocidad de desplazamiento controlada del pistón de 5mm/min. Por cada configuración, tres pruebas fueron realizadas, para un total de 18 ensayos. Para la fabricación de los tubos de metal expandido las mallas fueron concéntricamente enrolladas y cortadas hasta obtener la geometría correspondiente, así como un peso equivalente en relación con los tubos sólidos (Figura 1).

El acero ASTM A569 fue el material base empleado para la fabricación de los tubos de metal expandido mientras que los tubos con láminas sólidas fueron obtenidos comercialmente de un acero ASTM A500a y subsecuentemente cortados hasta obtener las longitudes requeridas como se indica en la Tabla 1. Las propiedades mecánicas obtenidas experimentalmente mediante tracción revelaron que ambos materiales están acordes con lo establecido en las Normas ASTM A1011/A1011M-03a [25].

Figura 1. Sección transversal: (a) tubos enrollados de metal expandido; (b) tubos sólidos. Fuente: Elaboración propia.

Los extremos de cada tubo fueron maquinados para proporcionar una superficie plana en el contacto con las placas superior e inferior de la máquina de ensayo. Un estudio desarrollado por Aalberg y Haugen [26], determinó que el efecto de las condiciones de borde en probetas de metal expandido sometidas a compresión (con y sin placas en los extremos) genera una respuesta semejante en la carga máxima y en el comportamiento posterior a la precitada carga, excepto que en aquellos especímenes con placas en los extremos los ensayos se podían continuar con mayores desplazamientos. De conformidad con lo anterior, en este estudio no se consideró la soldadura de placas en los extremos de las geometrías analizadas. En la Tabla 1, se presentan el promedio de las dimensiones para los tubos evaluados.

Tabla 1. Dimensiones promediadas de los tubos circulares.

Tubos	α (°)	L (mm)	D (mm)	e (mm)	W (g)
TCE0	0	304,90	121,50	1,41	1050,76
TCE60	60	304,50	110,93	1,43	1103,43
TCE90	90	304,10	103,83	1,42	1018,56
TCE90/60	90/60	303,33	96,14	1,43	1045,96
TCE60/90	60/90	304,66	98,60	1,44	1058,76

α=orientación de las celdas; L= altura; D= diámetro exterior; e= espesor; W= masa.

Fuente. Elaboración propia.

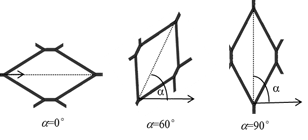
Figura 2. Orientación de celdas para los tubos de metal expandido y tubos sólidos. Fuente. [4].

Los tubos enrollados de metal expandido fueron evaluados para los siguientes ángulos de celdas individuales: α=0°, α=60°, α=90° y mediante la combinación de celdas: α=90°/60° y α=60°/90° (Figura 2). De estas celdas combinadas, en la primera consideración, las celdas con α=90° se localizan en el lado exterior del tubo mientras que las celdas con α=60°, en el lado interior. Para la segunda combinación, es lo opuesto. Las dimensiones de las celdas de metal expandido utilizado fueron las siguientes: eje mayor dh: 65,20mm; eje menor dv: 27,50mm; avance a: 1,05mm y espesor e: 2,50mm (Figura 3).

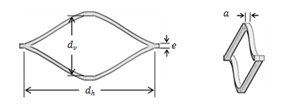
Figura 3. Nomenclatura de una celda: (a) vista frontal, (b) vista lateral. Fuente. Elaboración propia.

Como se mencionó anteriormente, la capacidad de carga fue evaluada en dos niveles:

• Carga máxima Pmáx [1]: definida como la carga máxima inicial necesaria para causar una deformación permanente. Esta carga fue obtenida directamente de las curvas carga-desplazamiento (Figura 4).

• Carga media Pm [1]: obtenida mediante la integración de la carga constante equivalente medida sobre la sección deformada;

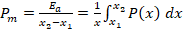(1)

donde Ea representa la energía total absorbida y P(x) el valor de la carga entre la longitud x1 y x2 de los tubos comprimidos.

Asimismo, se analizaron varios parámetros de resistencia al impacto para comparar los materiales y geometrías ensayadas en relación con su capacidad de absorción de energía. Las características de resistencia al impacto se estimaron a través de varios conceptos de diseño estructural como:

• Energía total absorbida Ea [1]: calculada mediante la integración de la curva carga-desplazamiento;

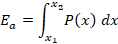
(2)

• Energía específica E_s [20]: definida como la energía absorbida por unidad de masa original no deformada W;

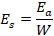
(3)

• Energía absorbida por unidad de longitud inicial E_Li [20]: denotada como la energía total absorbida por la longitud inicial no deformada;

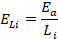
(4)

• Energía absorbida por unidad de longitud comprimida E_Lc [21]: definida como la energía total absorbida por la longitud deformada L_c;

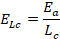
(5)

• Longitud de compactación por unidad de masa Lcm [24]: parámetro que relaciona la máxima distancia de compactación del absorbedor con respecto a su masa original no deformada W;

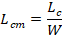
(6)

• Eficiencia estructural η_e [1]: referida también como eficiencia de carga. Es una medida de las fluctuaciones de carga que ocurren durante el aplastamiento de una estructura. Es calculada mediante la relación entre la carga media P_m y la carga máxima P_máx;

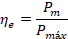
(7)

• Eficiencia de energía η_E [23]: definida como la relación entre la energía absorbida y la energía teórica máxima que puede ser absorbida. Es equivalente a la eficiencia estructural η_e.

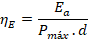
(8)

• Eficiencia de compactación η_c [22]: conocida también como eficiencia geométrica. Es un indicador del desempeño de un absorbedor de energía al ser comprimido. Es obtenida por la relación entre la longitud máxima deformada L_c de la probeta con respecto a la longitud inicial no deformada L_i;

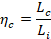
(9)

• Eficiencia total η_t [22]: obtenida por el producto de la eficiencia estructural η_e y la eficiencia de compactación η_c;

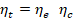
(10)

Metodología de análisis multi-criterio. Determinación de los pesos por AHP

El cálculo del peso individual por cada criterio w_j, fue obtenido mediante el método AHP por exhibir resultados más confiables en comparación con otros métodos probados [27]. Este método utiliza comparaciones por pares simples que permiten un análisis simultáneo de dos elementos [28,29].

Cuando las comparaciones entre los pares son consistentes, es posible obtener estructuralmente el orden de importancia de las mismas, en caso contrario deben revalorarse y corregirse los juicios iniciales. Estas comparaciones son fundamentadas en una escala relacional según el orden de importancia relativa [30] tal como se muestra en la Tabla 2.

Tabla 2. Escala de importancia relacional para el método AHP.

Importancia relativa	Calificación	Recíproco
El objetivo de i y j son de igual importancia	1	1
El objetivo i es ligeramente más importante que j	3	1/3
El objetivo i es fuertemente más importante que j	5	1/5
El objetivo i es muy fuertemente más importante que j	7	1/7
El objetivo i es absolutamente más importante que j	9	1/9
Valores intermedios	2,4,6,8

Fuente: Ishizaka y Lusti [30].

A continuación se detallan los pasos desarrollados para la aplicación del método AHP:

Paso 1. Construcción de la matriz de comparación por pares utilizando la escala de importancia relacional

La matriz de comparación por pares entre n elementos por cada nivel se construyó estableciendo una aproximación de cada a_ij=w_i/w_j. Esta relación permitió establecer el peso adecuado del elemento i con respecto al elemento j.

Paso 2. Determinación del vector de peso o autovector principal

El vector peso estimado w se obtuvo al resolver el autovector:

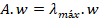
(11)

donde la matriz A consiste de todos los valores a_ij, y λ_máx es el autovalor principal de A. Si no hay inconsistencia entre el par de elementos, entonces a_ij es igual a 1/a_ij para cualquier i y j. El resultado es que λ_máx=n y A.w=n.w, donde n es el número de elementos en cada fila. Esta matriz se expresa como sigue:

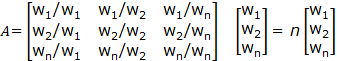
(12)

o puede ser también escrita en la forma:

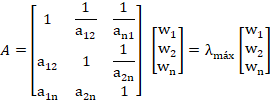
(13)

Para calcular el vector w (autovector) cada columna de la matriz A fue normalizada y promediada sobre sus filas. Este vector se usó para determinar la importancia a de cada elemento.

Paso 3. Cálculo del índice de consistencia IC

En la matriz recíproca consistente, el mayor autovalor es equivalente al tamaño de la matriz comparación o λ_máx=n. A esto se le conoce como índice de consistencia IC o grado de desviación de la matriz. Se expresa como sigue:

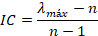
(14)

Paso 4. Cálculo de la relación de consistencia RC

La relación de consistencia RC [28], fue obtenida a partir del índice de consistencia IC y el índice de consistencia aleatorio IA (Tabla 3) en la forma:

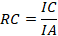
(15)

En la relación anterior, si el valor de la relación de consistencia RC es menor o igual a 10%, el juicio es aceptable, en caso contrario éste debe revalorado y refinado hasta un nivel operacional aceptable [28].

Tabla 3. Índice aleatorio IA.

n	1	2	3	4	5	6	7	8	9	10
IA	0,00	0,00	0,58	0,90	1,12	1,24	1,32	1,41	1,45	1,49

Fuente: Saaty [28].

Selección de la mejor alternativa por el método COPRAS

El método COPRAS supone dependencias directas y proporcionales según la significancia y grado de utilidad de las alternativas disponibles bajo la presencia de criterios mutuamente contradictorios [31]. Este método permite seleccionar la mejor decisión teniendo en cuenta separadamente la influencia de criterios de maximización y/o minimización cuantificando la solución de las alternativas con bastante precisión [32]. Consiste de los siguientes pasos:

Paso 1. Construcción de la matriz inicial X y cómputo del coeficiente relativo R

La construcción de la matriz inicial X permite priorizar las alternativas para la selección de los criterios tal como se muestra:

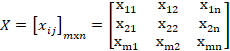
i=1,..,m

j=1,..,n

(16)

donde x_ij es el valor de desempeño de la i^ésima alternativa sobre el j^ésimo criterio, m es el número de alternativas confrontadas y n es el número de criterios. Un problema común se presentó en la selección de los criterios para el diseño de la matriz en virtud de que la mayoría no presentaba las mismas dimensiones. Para solventar este inconveniente la matriz X fue modificada por una matriz adimensionalizada r como sigue:

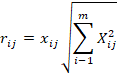
i=1,..,m

j=1,..,n

(17)

Paso 2. Cálculo de la matriz de decisión de peso normalizada

El valor normalizado de las ponderaciones 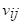fue determinado como sigue:

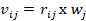
i=1,..,m

j=1,..,n

(18)

donde 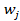es el peso de todos los j^ésimso criterios o atributos.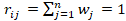

Paso 3. Determinación de la matriz decisión de peso normalizada D

La suma de los valores normalizados de peso adimensionales en cada criterio es siempre igual al peso por cada criterio como sigue:

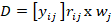
(19)

donde r_ij es el valor normalizado de la i^ésima alternativa sobre el j^ésimo criterio, y w_jes el peso del j^ésimo criterio tal como se indicó en la Ec. (16).

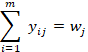
(20)

El cálculo del peso individual para cada criterio w_j, fue detallado en el epígrafe correspondiente al método AHP.

Paso 4. Sumatoria de los atributos beneficiosos y no-beneficiosos

Los atributos beneficiosos y no-beneficiosos son obtenidos de la matriz de decisión. Según corresponda, los atributos beneficiosos y no beneficiosos están asociados a una maximización o minimización de los criterios como sigue:

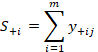
	(21)
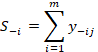
	(22)

donde y_+ij y y_-ij, son los valores de peso normalizados de los atributos beneficiosos y no-beneficiosos, respectivamente. Según sea el caso, el mayor valor de S_+i, podría resultar el mejor concepto de diseño cuando se desea maximizar el criterio, mientras que el menor valor de S_-i, también podría resultar el mejor concepto de diseño cuando el objetivo es la minimización de un criterio. Es de hacer notar que ∑S_+i y ∑S_-i respectivamente son siempre iguales a la sumatoria de los pesos para los atributos beneficiosos y no-beneficiosos tal como se denota a continuación:

Tabla 4. Caracterización de la capacidad de absorción de energía para las geometrías analizadas.

Tubos	Criterios
Tubos	P_máx (kN)	P_m (kN)	E_a (kJ)	E_s (kJ/kg)	E_Li (kJ/m)	E_Lc (kJ/m)	L_cm (m/kg)	η_e	η_E	η_c	η_t
TCE0	1,2567	1,0800	0,1583	0,1507	0,5193	1,0845	0,1389	0,8594	0,0640	0,4788	0,4115
TCE60	9,0917	4,3000	0,6297	0,5706	0,0021	4,3128	0,1323	0,4730	0,0129	0,4795	0,2268
TCE90	5,9600	2,4233	0,3553	0,3488	1,1683	2,4335	0,1433	0,4066	0,0177	0,4801	0,1952
TCE90/60	8,1200	5,5000	0,8058	0,7704	2,6566	5,5193	0,1396	0,6773	0,0094	0,4813	0,3260
TCE60/90	10,3733	6,1100	0,8950	0,8453	2,9377	6,1301	0,1379	0,5890	0,0072	0,4792	0,2823
TCS	80,0333	42,4800	6,2155	5,9359	20,3935	42,5721	0,1394	0,5308	0,0051	0,4790	0,2543

Fuente. Elaboración propia.

(a) TCE

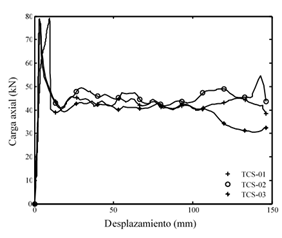
(b) TCS

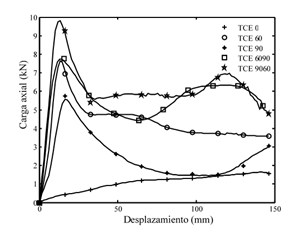
Figura 4. Curvas carga-desplazamiento para tubos ensayados: (a) metal expandido TCE; (b) sólido TCS. Fuente. Smith et al. [33].


δ =20mm

δ =140mm
(a) TCE0	(b) TCE060°	(c) TCE090°	(d) TCE09060	(e) TCE06090	(f) TCS

Figura 5. Evolución de la deformación: tubos de metal expandido y sólidos. Fuente. Smith et al. [33].

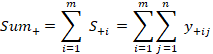
	(23)
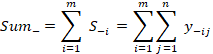
	(24)

La sumatoria de las ecuaciones (23) y (24) respectivamente, es siempre igual a uno.

Paso 5. Cálculo de la significancia relativa Q_i.

El mayor valor de significancia relativa Q_i representa la mejor opción. La significancia relativa es expresada como sigue:

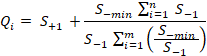
(25)

donde S_-min es el valor mínimo de S_-i

El cálculo de la utilidad cualitativa U_i está directamente relacionado con el valor Q_i señalado en la Ec. (26), de donde se aprecia que la misma es directamente proporcional a la significancia relativa. El máximo valor de significancia relativa es denotado como Q_máx.

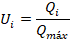
(26)

RESULTADOS Y DISCUSIÓN

Características de las curvas carga-desplazamiento

La Tabla 4 presenta un resumen de los parámetros de carga y resistencia de las geometrías analizadas [33]. Las Figuras 4a y 4b muestran las curvas típicas de carga-desplazamiento para los tubos de metal expandido (promediadas) y para los tubos sólidos ensayados. Correspondientemente, las Figuras 5a a 5f presenta la evolución de la deformación y el estado final de colapso de cada uno de los tubos ensayados.

Como se observa en la Figura 4a, el comportamiento de las curvas para los tubos enrollados de metal expandido con celdas individuales (TCE0, TCE60 y TCE 90) y combinadas (TCE6090 y TCE9060) depende de la orientación de las celdas con respecto a la dirección de aplicación de la carga. Se observa que la geometría y parámetros del material tienen un efecto directo en los niveles de carga y capacidad de absorción de energía. En particular, los tubos con celdas individuales TCE0 presentan una respuesta estructural más estable desde el dominio elástico hasta la zona plástica en comparación con las otras configuraciones. En contraste, los tubos con láminas sólidas (Figura 4b), exhiben un régimen plástico muy inestable caracterizado por picos de cargas que fluctúan y por una significante pérdida de estabilidad al alcanzar la carga máxima. Analizando la respuesta estructural parta los tubos de metal expandido TCE60 y TCE90, se observa disminución significativa en la capacidad de carga una vez se alcanza la carga máxima. No obstante, para las geometrías con celdas combinadas TCE6090 y TCE9060, la reducción en la capacidad de carga es ligeramente menor.

Modos de colapso

Como se puede apreciar en las Figuras 5a a 5e, los modos de colapso para los tubos de metal expandido (TCE) se caracterizan por aplastamiento progresivo, pandeo de celdas individuales y pandeo global de las paredes del tubo. Mientras que para tubos de láminas sólidas (TCS) el modo de colapso fue mixto: pandeo axi-simétrico y pandeo no simétrico con un número variable de lóbulos circunferenciales (Figura 5f).

Absorción de energía y conceptos de diseño estructural

Para proporcionar una comparación en la respuesta de cada configuración, los valores de energía absorbida presentados en la Tabla 4, fueron calculados para un desplazamiento de 146mm.

Energía absorbida por unidad de longitud E_Li- E_Lc

La energía absorbida por unidad de longitud es un importante parámetro de resistencia al impacto a considerar cuando el espacio es una limitación. En la Tabla 4, la longitud inicial L_i y la longitud deformada L_cfue la misma para todas las geometrías. Se encontró que la longitud de los tubos no tiene un efecto significativo sobre la respuesta de aplastamiento y absorción de energía. Esto es obviamente debido a que los niveles de carga y energía absorbida están asociados a la geometría y parámetros del material. Como se esperaba, valores superiores de energía absorbida por unidad de longitud fueron computados en los tubos sólidos, seguidos por los tubos de metal expandido con celdas combinadas TCE6090 y TCE9060, mientras que en los tubos con celdas individuales la respuesta fue virtualmente menor. Es importante mencionar que el efecto de la longitud, puede ser eliminado considerando la energía específica E_s.

Energía específica E_s

La energía específica E_s es un parámetro a considerar cuando la reducción de peso es importante. Permite una comparación entre diferentes elementos para determinar cuál es el más eficiente en términos de la cantidad de energía que éstos pueden absorber para una masa dada. Como se observa en la Tabla 4, para niveles semejantes de masa, la energía específica E_s en los tubos sólidos TCS es de 5,9359 kJ/kg, mientras que en los tubos de metal expandido con celdas combinadas e individuales los valores promedio fueron 0,8078 kJ/kg y 0,3567 kJ/kg, respectivamente. La energía específica E_s de los tubos TCS es 7,33 veces superior a la de los tubos con celdas combinadas, y 16,5 veces más alta que la de los tubos con mallas individuales. No obstante, el hecho de que estos tubos posean una alta energía específica E_s, no significa que sean los más efectivos para absorber energía, considerando entre otras cosas que la energía específica también depende de la cantidad de material disponible para deformación plástica. Con base en lo anterior, es evidente que los tubos de metal expandido proporcionan menos material que los tubos sólidos para una misma longitud debido a las discontinuidades geométricas presentes. Por ello, para que la energía total de los tubos expandidos sea igual, éstos requerirán una cantidad de material mayor que los tubos sólidos y por lo tanto podrían demandar más espacio para su implementación, lo cual podría ser inadecuado en aplicaciones con espacios limitados.

Longitud de compactación por unidad de masa L_cm

Este parámetro proporciona una eficiente manera de comparación para distintos materiales con densidades diferentes. Está asociado a la estabilidad y repetibilidad de los modos de deformación cuando un dispositivo es sometido a cargas de trabajo inciertas en magnitud, dirección y distribución. Para el caso estudiado la densidad del material no varía, sin embargo las discontinuidades geométricas de las mallas podrían afectar los resultados. Así pues, en la Figura 5, se puede verificar que las geometrías estudiadas presentan modos característicos de evolución y deformación a través del proceso de colapso. En particular, los tubos TCE0 presentan un modo estable de aplastamiento (Figuras 5a) que permite que la absorción de energía sea alcanzada eficientemente mientras que las configuraciones TCE90, TCE6090, TCE9060 (Figuras 5b, 5c y 5d respectivamente) y en los tubos sólidos TCS (Figura 5f), se evidencian modos mixtos de aplastamiento dominados por pandeo, los cuales afectan la respuesta estructural de estos elementos. En la Tabla 5 se observa que la longitud de compactación por unidad de masa L_cm permanece constante para todas las configuraciones analizadas.

Eficiencia estructural η_e

En general, se buscan sistemas con valores de eficiencia estructural η_ecercanos a 1. Una maximización de este parámetro permite alcanzar una buena capacidad de absorber energía con una menor fuerza transmitida a la estructura que se intenta proteger. Esto se puede obtener disminuyendo la carga máxima inicial mediante la introducción de mecanismos de control de deformación. De la Tabla 4, se observa que la eficiencia estructural η_evaría en función de la geometría, se observa que los tubos de metal expandido TCE0 presentan el mayor valor de eficiencia estructural (η_e=0,8594), lo que indica que la capacidad de absorción de energía en estos modelos es alcanzada eficientemente. En contraste, para las geometrías restantes, la eficiencia estructural η_e es apreciablemente menor, η_e=0,4066 para TCE90 y η_e=0,6773 para TCE9060, debido a un aumento de la carga máxima, lo cual es indeseable en aplicaciones prácticas. Se destaca que el efecto de las celdas combinadas en los tubos expandidos mejora la eficiencia estructural η_e comparado con los tubos sólidos. Como resultado, la estabilidad y capacidad de éstos para soportar cargas es mejorada aumentando la cantidad de material disponible para deformación plástica.

Eficiencia de energía η_E

El parámetro adimensional de eficiencia de energía η_E fue adoptado para comparar la resistencia al impacto de las diferentes geometrías analizadas. De la Tabla 4, se encontró que la eficiencia de energía η_E en los tubos de metal expandido es significativamente mayor (η_E=0,064 para TCE0 y η_E=0,0072 para TCE6090) que en los tubos TCS los cuales presentaron el menor valor (η_E=0,0051). La Tabla 4, revela también que aun cuando en todos los casos, el valor de eficiencia de energía η_E fue mucho menor que uno, en los tubos de metal expandido TCE0, TCE 60 y TCE90 la eficiencia de energía fue mayor que en aquellos con celdas combinadas TCE6090 y TCE9060. En la Figura 4a, se observa que al alcanzar la carga máxima, la deformación de los tubos expandidos con celdas individuales es mayor que en los tubos con celdas combinadas y tubos con láminas sólidas (Figura 4b). En el caso de los tubos TCE0 (Figura 4a), esto ocurre porque una vez alcanzaron la máxima carga e inmediatamente después que el material fluyó, la fuerza de colapso se mantuvo constante al tiempo que el tubo se aplastaba. Se evidencia que la inclinación de las celdas en los tubos de metal expandido causa variaciones significativas en el nivel de absorción de energía y deformación, siendo más eficientes y con modos deformación más controlados para la orientación TCE0 (Figuras 5a).

Eficiencia de compactación η_c

La eficiencia de compactación η_c es un indicador de la cantidad de material que puede aprovecharse durante el proceso de colapso. Este parámetro sin embargo es dependiente de la energía cinética inicial. Idealmente los dispositivos de absorción de energía son diseñados para deformarse de forma compacta sobre toda su longitud, aunque en la realidad su relación de compactación es siempre menor a uno. En la Tabla 4, la eficiencia de compactación es en general baja para todos los tubos ensayados, va desde η_c=0,4788 para los tubos TCE0 hasta η_c=0,4813 para los tubos TCE9060, lo cual representa una variación de 0,5%. Comparando los tubos de metal expandido y tubos sólidos, la eficiencia de compactación η_c se mantiene casi invariable. Existe apenas un ligero aumento de la eficiencia η_c al aumentar el ángulo de la celda, a pesar de que los tubos con mallas inclinadas presentan mayor inestabilidad en sus colapsos, tal como se evidencia en las Figuras 5b a 5e. Es por ello que la compresibilidad y la deformación plástica de estos elementos es ligeramente mayor al igual que la eficiencia de compactación η_c. De lo anterior se desprende que las características de resistencia al impacto pueden ser maximizadas usando dispositivos de absorción de energía con alta eficiencia estructural y alta eficiencia de compactación η_c.

Eficiencia total η_t

La eficiencia total es una medida integrativa de la eficiencia estructural y la eficiencia de compactación [22]. De la Tabla 4, la eficiencia integral para los tubos TCE0 es η_t=0,4115, y para los tubos TCE6090 y TCE9060 presentan una eficiencia integral de η_t=0,2823 y η_t=0,3260, respectivamente, las cuales son superiores a las de los tubos TCS (η_t=0,2543). Esto se debe a que los tubos de metal expandido proporcionan una razonable carga de colapso constante, lo cual es una característica altamente deseable en situaciones de resistencia al impacto. Pese a que los tubos sólidos presentaron mayores valores en la eficiencia de compactación η_c y carga máxima inicial P_máx, su eficiencia total η_t resultó ser razonablemente baja.

Selección del mejor perfil para aplicaciones de absorción de energía

El análisis multi-criterio se fundamentó en el método AHP para la asignación de pesos a los criterios y en el método COPRAS para seleccionar la alternativa ideal entre las opciones disponibles. Los detalles de ambos métodos fueron descritos anteriormente. Del total de parámetros evaluados en la Tabla 4, seis criterios fueron establecidos luego de un exhaustivo análisis: carga máxima P_máx, longitud de compactación por unidad de masa L_cm, eficiencia estructural η_e, eficiencia de compactación η_c,eficiencia de energía η_E y eficiencia total η_t. En la Tabla 5, se presenta el análisis por pares para cada criterio según el método AHP. Subsecuentemente en la Tabla 6, se presenta la matriz normalizada y el vector prioridad.

Tabla 5. Matriz de comparación por pares para cada criterio según AHP.

Criterios	P_máx	L_cm	η_e	η_E	η_c	η_t
P_máx	1,0000	0,2000	0,1111	0,1111	0,1429	0,1111
L_cm	5,0000	1,0000	0,1111	0,1111	0,2000	0,1111
η_e	9,0000	9,0000	1,0000	1,0000	3,0000	1,0000
η_E	9,0000	9,0000	1,0000	1,0000	3,0000	0,5000
η_c	7,0000	5,0000	0,3333	0,3333	1,0000	0,2000
η_t	9,0000	9,0000	1,0000	2,0000	5,0000	1,0000

Fuente. Elaboración propia.

Tabla 6. Matriz normalizada por pares según AHP.

Criterios	P_máx	L_cm	η_e	η_E	η_c	η_t	Vector prioridad
P_máx	0,0734	0,4487	0,6181	0,9320	0,4463	0,6170	0,0227
L_cm	0,5309	0,4274	0,3402	0,1878	0,4470	0,3400	0,0442
η_e	0,3480	0,4629	0,2924	0,2577	0,4475	0,2927	0,2637
η_E	0,4741	0,4509	0,4871	0,1369	0,4486	0,4888	0,2352
η_c	0,6057	0,4455	0,4236	0,1048	0,4467	0,4233	0,1070
η_t	4,6732	0,4503	0,3818	0,0743	0,4465	0,3813	0,3273

Fuente. Elaboración propia.

Tabla 7. Matriz de decisión normalizada.

Tubos	Criterios
Tubos	P_máx	L_cm	η_e	η_E	η_c	η_t
TCE0	0,0959	0,1671	0,2430	0,5503	0,1664	0,2427
TCE60	0,0724	0,1591	0,1338	0,1109	0,1666	0,1337
TCE90	0,0474	0,1724	0,1150	0,1522	0,1668	0,1151
TCE90/60	0,0646	0,1679	0,1915	0,0808	0,1672	0,1920
TCE60/90	0,0826	0,1659	0,1666	0,0619	0,1665	0,1665
TCS	0,6371	0,1677	0,1501	0,0439	0,1664	0,1500

Fuente. Elaboración propia.

Tabla 8. Matriz de peso normalizada.

Tubos	Pesos
	0,0227	0,0442	0,2637	0,2352	0,1070	0,3273
	Criterios
	P_máx	L_cm	η_e	η_E	η_c	η_t
TCE0	0,0022	0,0074	0,0641	0,1294	0,0178	0,0794
TCE60	0,0016	0,0070	0,0353	0,0261	0,0178	0,0438
TCE90	0,0011	0,0076	0,0303	0,0358	0,0178	0,0377
TCE90/60	0,0015	0,0074	0,0505	0,0190	0,0179	0,0628
TCE60/90	0,0019	0,0073	0,0439	0,0146	0,0178	0,0545
TCS	0,0145	0,0074	0,0396	0,0103	0,0178	0,0491

Fuente. Elaboración propia.

Tabla 9. Suma de pesos normalizados.

Tubos	Atributos
Tubos	Beneficiosos S_i+	No-Beneficiosos S_i-
TCE0	0,2981	0,0022
TCE60	0,1300	0,0016
TCE90	0,1292	0,0011
TCE90/60	0,1576	0,0015
TCE60/90	0,1381	0,0019
TCS	0,1242	0,0145
∑Atributos	0,9772	0,0228

Fuente. Elaboración propia.

Tabla 10. Valores Q_i y U_i.

Tubos	Q	U	Rango
TCE0	0,3013	100,00	1
TCE60	0,1342	44,54	5
TCE90	0,1357	45,03	4
TCE90/60	0,1624	53,89	2
TCE60/90	0,1418	47,06	3
TCS	0,1247	41,38	6

Fuente. Elaboración propia.

Los atributos beneficiosos y no-beneficiosos, son presentados en las Tabla 9. En este caso el único atributo no beneficioso fue el criterio de carga máxima P_máx donde un valor más bajo debe ser preferido. El resultado final o utilidad cuantitativa U_i para cada geometría, es presentado en la Tabla 10.Con base en los resultados obtenidos en la Tabla 10, la solución más óptima para el diseño de un dispositivo de absorción de energía eficiente es el tubo de metal expandido con celdas individuales TCE0, seguido por aquellos de celdas combinadas con orientación TCE9060. El concepto más deficiente resultó el perfil con láminas sólidas TCS.

CONCLUSIONES

En este trabajo se evaluó la respuesta estructural de tubos circulares fabricados con láminas de metal expandido y láminas sólidas sometidos a cargas axiales cuasi-estáticas de compresión. Se encontró que variaciones en la geometría, dirección de las celdas de las láminas de metal expandido y el tipo de material, juegan un rol importante en la capacidad de carga, resistencia al impacto, eficiencia y modos de colapso de los tubos analizados. Para los tubos de metal expandido con celdas individuales, la absorción de energía específica y energía por unidad de longitud no es tan buena como en los tubos con celdas combinadas y tubos sólidos. Una comparación de los factores de eficiencia, revela que la capacidad de absorción de energía de los tubos de metal expandido con celdas individuales y orientación α=0° es significativamente mayor. Para los tubos con láminas sólidas, la carga máxima alcanzada es mayor. Sin embargo, al alcanzar dicha carga, ocurre una significante reducción de su estabilidad. Rotación lateral, pandeo irregular axi-simétrico de las celdas y flexión en el eje de los tubos de metal expandido con TCE60, TCE90, TCE6090 y TCE 9060, permiten identificar nuevos modos de deformación mixtos que están dominados por pandeo. No obstante, los tubos de metal expandido con celdas individuales TCE0 exhibieron un modo de deformación progresivo por lo cual su respuesta estructural fue más controlada y estable que el resto de los modelos estudiados.

Mediante las técnicas de análisis multi-criterio por los métodos AHP y COPRAS se evaluaron diferentes parámetros de carga y resistencia de impacto para encontrar un diseño geométrico óptimo en aplicaciones de absorción de energía. Los resultados indican que los tubos de metal expandido con celdas individuales TCE0 resultan ser la solución más ideal para que la capacidad de absorción de energía sea alcanzada eficientemente. La metodología de análisis multi-criterio constituye una valiosa herramienta de apoyo para derivar la respuesta final en los procesos de toma de decisiones para la selección de dispositivos o componentes empleados en aplicaciones de absorción de energía y en muchas otras aplicaciones científicas y de ingeniería.

AGRADECIMIENTOS.

Los autores quieren agradecer al Laboratorio de: Ciencias de los Materiales, Herrería y Soldadura, y al Centro de Investigaciones Tecnológicas de la Universidad Nacional Experimental Francisco de Miranda, por el apoyo prestado.

REFERENCIAS

[1] C. Graciano, G. Martínez and D. Smith, “Experimental investigation on the axial collapse of expanded metal tubes,” Thin-Walled Structures, vol. 47, no. 8-9, pp. 953-961, Ago-Sep, 2009.

[2] A,A,A. Alghamdi, “Collapsible impact energy absorbers: an overview,” Thin-Walled Structures, vol. 39, no. 2, pp. 189-213, Feb, 2001.

[3] A. Olabi, E. Morrisa and M. Hashmi, “Metallic tube type energy absorbers: a synopsis,” Thin-Walled Structures, vol. 45, no. 7-8, pp. 706-726, Jul-Ago, 2007.

[4] D. Smith, C. Graciano and G. Martínez, “Quasi-static axial compression of concentric expanded metal tubes,” Thin-Walled Structures, vol. 84, pp. 70-76, 2014.

[5] D. Smith, C. Graciano, G. Martínez and P. Teixeira, “Axial crushing of flattened expanded metal tubes,” Thin Walled Structures, vol. 85, pp. 42-49, Dec. 2014.

[6] D. Smith, C. Graciano and G. Aparicio, “An empirical method for the estimation of yield strength on expanded metal meshes,” Rev. Fac. Ing. Univ. Ant. vol. 74, pp. 161-171, 2015.

[7] D. Smith, C. Graciano and G. Aparicio, “Energy absorption capacity of expanded metal meshes subjected to tensile loading,” Rev. Fac. Ing. Univ. Ant., vol. 77, pp. 48-53, 2015.

[8] N. M. Stefano, N. Casarotto Filho, L.G.L. Vergara and R.U.G. da Rocha, “COPRAS (Complex Proportional Assessment): state of the art research and its applications,” IEEE Latin America Transactions, vol. 13, no. 12, pp. 3899-3906, 2015.

[9] O. Taylan, A. Bafail, R. Abdulaal and M. Kabli, “Construction projects selection and risk assessment by fuzzy AHP and fuzzy TOPSIS methodologies,” Int J Appl Soft Comput, vol. 17, pp. 105-116, Apr, 2014.

[10] T. Boucher and E. McStravic, “Multi-attribute evaluation within a present value framework and its relation to the analytic hierarchy process,” Eng Econ, vol. 37, pp. 55-71, 1991.

[11] F. Tarlochan and F. Samer, “Design of thin wall structures for energy absorption applications: design for crash injuries mitigation using magnesium alloy,” Int J Res Eng Tech, vol. 2, no. 7, pp. 24-36. 2013.

[12] A. Mohammed, A. Hazem, and M. Ayman “Integrated Fuzzy (GMM) -TOPSIS model for best design concept and material selection process,” Int J Innov Res Sci Eng Technol, vol. 2, no. 11, pp. 6464-6486, 2013.

[13] G. Zheng, S. Wu, G. Sun, G. Li, and Q. Li, “Crushing analysis of foam-filled single and bitubal polygonal thin-walled tubes,” International Journal of Mechanical Sciences, vol. 87, pp. 226-240, Oct, 2014.

[14] N. Qiu, Y. Gao, J. Fang, Z. Feng, G. Sun, and Q. Li, “Crashworthiness analysis and design of multi-cell hexagonal columns under multiple loading cases,” Finite Elements in Analysis and Design, vol. 104, pp. 89-101. 2015.

[15] S. Pirmohammad, and S.E. Marzdashti, “Crushing behavior of new designed multi-cell members subjected to axial and oblique quasi-static loads,” Thin-Walled Structures, vol. 108, pp. 291-304, 2016.

[16] V. Gadakh, “Parametric optimization of wire electrical discharge machining using TOPSIS method,” Adv Produc Eng Manag, vol. 7, no. 3, pp. 157-164, 2012.

[17] L. Wang, T. Raz, “Analytic hierarchy process based on data for problem,” Comput & IE, vol. 20, pp. 355-365, 1991.

[18] V. Tarigopula, M. Langseth, O. Hopperstad, and A. Clausen, “Axial crushing of thin-walled high-strength steel sections,” Int J Impact Eng, vol. 32, pp. 847-882, 2005.

[19] A. Puglsey, “The crumpling of tubular structures under impact conditions,” In: Proc. of the Symposium on the use of aluminium in railway rolling stock. Institute of Locomotive Engineers. The Aluminium Development Association, pp. 22-41, 1960.

[20] S. Hosseinipour, G. Daneshi, “Energy absorption and mean load of thin-walled grooved tubes under axial compression,” Thin-Walled Structures, vol. 41, pp. 31-46, 2003.

[21] Z. Ahmad, “Impact and energy absorption of empty and foam-filled conical tubes,” Doctoral dissertation, Queensland University of Technology, 2009.

[22] Y. Lou, C. Park and H. Huh, “Parameter study on the quasi-statically axial crush of frusta with small semiapical angles using finite element method,” Annual Conference. The Korean Society of Automotive Engineers. [En línea]. Disponible en: http://koasas.kaist.ac.kr/bitstream/10203/19503/1/ck174.pdf, 2008.

[23] S. Chung, and G. Nurick, “The energy-absorbing characteristics of tubular structures with geometric and material modifications: An overview,” Appl Mech Rev, vol. 61, pp. 020802-1/020802-15, 2008.

[24] R.H. Smith Jr, “Energy absorption of sine wave beams subjected to axial impact loading,” Doctoral dissertation, Clemson University, 2007.

[25] ASTM A1011/A1011M-03a: Standard speciﬁcation for steel, sheet and strip, hot-rolled, carbon, structural, high-strength low-alloy and high-strength low-alloy with improved formability. ASTM International, West Conshohoken, PA, 2003.

[26] A. Aalberg, and B. Haugen, “An experimental investigation of a rectangular hollow steel section with solid corners and expanded metal sections,” Norwegian University of Science Technology. Technical Report, R-8-97, p. 1-77, 1997.

[27] S. Tung, and S. Tang, “Comparison of the saaty’s AHP and modified AHP for right and left eigenvector inconsistency,” European Journal of Operational Research, vol. 106, no. 1, pp. 123-128, 1998.

[28] T. Saaty, The analytic hierarchy process. Ed. McGraw-Hill, New York, 1980.

[29] T. Saaty, “Priority setting in complex problems,” IEEE Trans. Eng. Manag, vol. 30, no. 3, pp. 140-155, 1983.

[30] A. Ishizaka and M. Lusti, “An intelligent tutoring system for AHP,” Proceedings of the 9th international conference on operational research. University of Osijek, Croatia, pp. 215-223, 2003.

[31] E. Zavadskas and A. Kaklauskas, Multicriteria evaluation of building, Technika Vilnius, 1996.

[32] P. Chatterjee, V. Manikrao and S. Chakraborty, “Materials selection using complex proportional assessment and evaluation of mixed data methods,” Mater Design, vol. 32, pp. 851-860, 2011.

[33] D.J Smith, C.A. Graciano, P. Teixeira, G. Martínez and A. Pertuz, “Energy absorption characteristics of coiled expanded metal tubes under axial compression,” Latin American Journal of Solids and Structures, vol. 13, no. 16, pp. 3145-3160, 2016.

RESUMEN

ABSTRACT

INTRODUCCIÓN

TÉCNICAS EXPERIMENTALES

Condiciones de ensayo y propiedades de los materiales

Metodología de análisis multi-criterio. Determinación de los pesos por AHP

Selección de la mejor alternativa por el método COPRAS

RESULTADOS Y DISCUSIÓN

Características de las curvas carga-desplazamiento

Modos de colapso

Absorción de energía y conceptos de diseño estructural

Energía absorbida por unidad de longitud E_Li- E_Lc

Energía específica E_s

Longitud de compactación por unidad de masa L_cm

Eficiencia estructural η_e

Eficiencia de energía η_E

Eficiencia de compactación η_c

Eficiencia total η_t

Selección del mejor perfil para aplicaciones de absorción de energía

CONCLUSIONES

AGRADECIMIENTOS.

REFERENCIAS

RESUMEN

ABSTRACT

INTRODUCCIÓN

TÉCNICAS EXPERIMENTALES

Condiciones de ensayo y propiedades de los materiales

Metodología de análisis multi-criterio. Determinación de los pesos por AHP

Selección de la mejor alternativa por el método COPRAS

RESULTADOS Y DISCUSIÓN

Características de las curvas carga-desplazamiento

Modos de colapso

Absorción de energía y conceptos de diseño estructural

Energía absorbida por unidad de longitud ELi - ELc

Energía específica Es

Longitud de compactación por unidad de masa Lcm

Eficiencia estructural ηe

Eficiencia de energía ηE

Eficiencia de compactación ηc

Eficiencia total ηt

Selección del mejor perfil para aplicaciones de absorción de energía

CONCLUSIONES

AGRADECIMIENTOS.

REFERENCIAS

Energía absorbida por unidad de longitud E_Li- E_Lc

Energía específica E_s

Longitud de compactación por unidad de masa L_cm

Eficiencia estructural η_e

Eficiencia de energía η_E

Eficiencia de compactación η_c

Eficiencia total η_t