Aplicación de campos estocásticos en problemas de
geotecnia
Application of
stochastic fields in geotechnical problems
Jorge Luis
Palomino-Tamayo1, Armando Miguel Awruch 2, Wilson
Rodríguez-Calderón3
1Centro de Mecánica Aplicada y
Computacional - CEMACOM, Facultad de Ingeniería Civil, Universidad Federal do
Rio Grande do Sul-UFRGS, Porto Alegre/RS, Brasil. Email: jorgetamayo@ufrgs.br
Centro de Mecánica Aplicada y Computacional - CEMACOM, Facultad de
Ingeniería Civil, Universidad Federal do Rio Grande do Sul-UFRGS, Porto
Alegre/RS, Brasil. Email: amawruch@ufrgs.br
Centro de Mecánica Aplicada y
Computacional - CEMACOM, Facultad de Ingeniería Civil, Universidad Federal do
Rio Grande do Sul-UFRGS, Porto Alegre, Brasil. Email: wilroca50@hotmail.com
RESUMEN
Este trabajo se enfoca en el análisis
probabilístico de problemas de estabilidad de taludes y de asentamientos
producidos en zapatas rígidas apoyadas en suelos deformables. Para este
propósito son estudiados y combinados modelos matemáticos basados en el Método
de los Elementos Finitos (MEF), método de Montecarlo (MC) y en el procedimiento
de Subdivisión de Media Local (LAS). La metodología LAS se utiliza para generar
campos estocásticos que representen apropiadamente las incertidumbres asociadas
a las propiedades de los materiales. La utilización del MEF permite obtener la
respuesta numérica del problema en términos de desplazamientos y tensiones. La
plasticidad del suelo puede ser incluida a través de un algoritmo visco-plástico
conjuntamente con el criterio de plastificación de Mohr-Coulomb. Los
procedimientos LAS y MEF están incorporados dentro del marco de análisis del
método de Montecarlo, donde cada análisis requiere la ejecución de varias
simulaciones numéricas del problema en cuestión. Todo esto a fin de cuantificar
una probabilidad de falla y el asentamiento más probable a ocurrir en el caso
de problemas de cimentaciones. De los estudios realizados, se sugiere utilizar
al menos 4000 y 500 simulaciones para los problemas del talud y zapata,
respectivamente, a fin de obtener resultados estables y confiables. Los
resultados obtenidos muestran que la probabilidad de falla para el talud
estudiado está alrededor de 0.18, mientras que el asentamiento más probable a
ocurrir para un sistema suelo-zapata en condiciones de servicio está alrededor
de 1.96 cm.
PALABRAS
CLAVE: Campos
estocásticos, Elementos finitos, Análisis probabilístico, Geotecnia.
ABSTRACT
This work focuses on the probabilistic analysis of slope
stability and rigid shallow footing problems. For this purpose, mathematical
models based on the Finite Element Method (FEM), Montecarlo (MC) method and
Local Average Subdivision (LAS) procedure are studied. The LAS procedure is
used to generate random fields, which properly represent the associated
uncertainties in the properties of the materials. The FEM focuses on the
numerical response of the problem in terms of displacements and stresses. The
plasticity of the soil can be included via a visco-plastic algorithm beside a
Mohr-Coulomb law. The LAS and FEM procedures are implemented in the framework
of a MC analysis, where each MC execution requires several simulations of the
problem at hand. This permits to quantify the failure probability of the system
and report the most probable settlement to occur in the case of shallow
foundations. After many executions of the numerical model, it is suggested that
at least 4000 and 500 simulations are needed for the slope stability and
shallow foundation problems, respectively, in order to obtain stable and
reliable values. The obtained results show that the failure probability of the
slope is relatively low and equal to 0.18, while the expected settlement of a shallow
rigid foundation is around 1.96 cm.
KEYWORDS:
Stochastic field,
Finite element, Probabilistic analysis, Geotechnics.
INTRODUCCIÓN
Es importante cuantificar la
confiabilidad de los sistemas estructurales frente a la posible aleatoriedad de
las propiedades de los materiales. Esto último es relevante en el caso de los
suelos y rocas debido a la alta variabilidad de sus propiedades principalmente
en su estado natural. Por ejemplo, en una situación hipotética donde no existen
restricciones económicas, es posible seleccionar algunas muestras de suelo de
la zona del problema en estudio y determinar en laboratorio, las propiedades
más importantes del material tales como su permeabilidad, compresibilidad,
resistencia al corte, entre otras. Con esa información disponible es posible
simular el problema numéricamente y tener un grado alto de confiabilidad en los
resultados obtenidos. Sin embargo, en la práctica común se cuenta apenas con
pocos datos de campo y laboratorio, siendo el enfoque usual considerar valores
característicos para las propiedades de los materiales, conjuntamente con un
factor de seguridad. De hecho, la mayoría de las normas de diseño siguen este
enfoque.
En la literatura especializada existen
varios enfoques para estudiar el problema de confiabilidad estructural, dentro
de la grande diversidad de métodos, podemos citar el método llamado en la
literatura inglesa de Random Finite Element Method (RFEM, Fenton y
Griffith, 2008, Paiboon 2013, Bari 2012), el cual es utilizado en este trabajo.
Este método combina la técnica MEF y MC con un generador de campos estocásticos
basado en el procedimiento LAS. La metodología ha sido aplicada extensamente
por otros investigadores para el estudio y análisis de problemas de estabilidad
de taludes, cimientos, flujo a través de presas y licuefacción de suelos, entre
otros. El método LAS es capaz de lanzar procesos aleatorios a nivel local en
cada elemento finito que compone la malla. Las rutinas de computador
disponibles en Fenton y Griffith (2008) son utilizados en este trabajo para
simular el comportamiento probabilístico de un talud y de un sistema
suelo-zapata.
Existen otras metodologías para el
estudio de confiabilidad estructural o riesgo, dentro de estas técnicas se
puede mencionar la técnica llamada en la literatura inglesa de First Order
Realiability Method (FORM), simulación directa de Montecarlo y simulación
de Montecarlo con muestreo por importancia adaptativo (MCIS), entre otras.
Cavalcante et al. (2005) estudio el análisis de riesgo en taludes
utilizando el método de Montecarlo, PEM (Point
Estimate Method) y la teoría de conjuntos difusos. Bressani y Costa (2005)
estudiaron probabilísticamente la estabilidad de un talud coluvionar de basalto
siguiendo una metodología que incluye un análisis determinista inicial,
caracterización de las variables de entrada (simulación de las incertidumbres y
correlación) y aplicación de método probabilístico
con método de Montecarlo. Temas probabilísticos también han sido destinados a
la estimación del daño sísmico en puentes (Lamus et al. 2012).
MÉTODOS
Modelamiento
estocástico
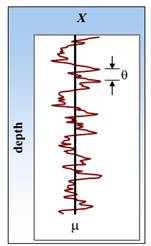
En la Fig. 1 se ilustran las propiedades
estadísticas de una arcilla no drenada, la cual es caracterizada por su
resistencia al corte no drenada, X = cu. La Fig. 1(a)
muestra la variación de esta cohesión cu con la profundidad
de un depósito de suelo uniforme. En el caso de un proyecto convencional, se
consideraría apenas la media, 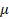 , de esta propiedad en el análisis numérico o algún otro valor
característico sugerido por alguna norma de diseño. Sin embargo, en un proyecto
estocástico todas las propiedades de los materiales o por lo menos las más
importantes deben ser representadas a través de su media y desviación estándar
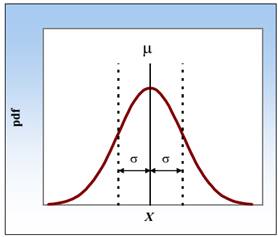
como se ilustra en la Fig. 1(b). En este último caso, la variabilidad de las
propiedades es expresada en términos de las funciones de densidad de
probabilidad (pdf), las cuales son precisamente caracterizadas por la media μ y
una desviación estándar normalizada, σ. Estas consideraciones definen el
llamado coeficiente de variación V mostrado en la Ec.1.
, de esta propiedad en el análisis numérico o algún otro valor
característico sugerido por alguna norma de diseño. Sin embargo, en un proyecto
estocástico todas las propiedades de los materiales o por lo menos las más
importantes deben ser representadas a través de su media y desviación estándar
como se ilustra en la Fig. 1(b). En este último caso, la variabilidad de las
propiedades es expresada en términos de las funciones de densidad de
probabilidad (pdf), las cuales son precisamente caracterizadas por la media μ y
una desviación estándar normalizada, σ. Estas consideraciones definen el
llamado coeficiente de variación V mostrado en la Ec.1.
|
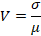
|
(1)
|
La función de densidad de probabilidad
mostrada en la Fig. 1 (b) sigue una distribución normal, aunque otras distribuciones
del tipo log-normal, exponencial, beta, entre otras, podrían ser utilizadas a
fin de mejorar la representación espacial de las propiedades. Los conceptos de
media y desviación estándar son también utilizados para describir la variación
de los parámetros de resistencia con la profundidad 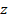 de un depósito de suelo. Por ejemplo, Lumb (1966) consideró una
tendencia lineal para una arcilla no drenada de la siguiente manera:
de un depósito de suelo. Por ejemplo, Lumb (1966) consideró una
tendencia lineal para una arcilla no drenada de la siguiente manera:
|
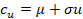
|
|
(2)
|
donde 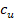 es la resistencia al corte no drenada y:
es la resistencia al corte no drenada y:
|
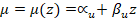
|
(3)
|
|
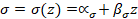
|
(4)
|
con 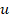 siendo una variable aleatoria normalizada con media cero y
desviación estándar unitaria, la cual varía de acuerdo con el tipo de función
de densidad de probabilidad seleccionada. Para una distribución normal, esta
función se define por la Ec. 5. Donde
siendo una variable aleatoria normalizada con media cero y
desviación estándar unitaria, la cual varía de acuerdo con el tipo de función
de densidad de probabilidad seleccionada. Para una distribución normal, esta
función se define por la Ec. 5. Donde 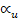 ,
,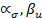 y
y 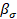 en las ecuaciones 3 y 4 representan parámetros que definen la
variación de la media y desviación estándar, respectivamente, de la propiedad
en cuestión con la profundidad del suelo.
en las ecuaciones 3 y 4 representan parámetros que definen la
variación de la media y desviación estándar, respectivamente, de la propiedad
en cuestión con la profundidad del suelo.
|
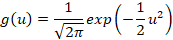
|
(5)
|
|
|
|
|
a) 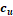 como función de la
profundidad z como función de la
profundidad z
|
b) Función de densidad de probabilidad de 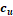
|
c) Figura 1. Representación de la variabilidad de la resistencia al corte
no drenada 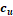 del suelo. Fuente. Elaboración propia.
del suelo. Fuente. Elaboración propia.
En la Ec. (3), para que la media cu
sea constante con la profundidad (como se representa por la línea negra en la
Fig. 1 (a)), se requiere que βu sea zero, mientras que αu
= ασ = 0 permite que μ y σ se incrementen
linealmente desde valores nulos en la superficie del suelo (en z = 0).
En este caso, el coeficiente V = βσ
/ βμ de la Ec. 1 adopta un valor constante a lo largo de la
profundidad.
De esta manera, las ecuaciones (1)-(5)
definen parcialmente la variabilidad de las propiedades en el dominio espacial,
pero también se requiere de la definición de un parámetro estadístico
adicional, θ, que define el grado de correlación espacial entre las
zonas adyacentes (Vanmarcke, 1983, Vanmarcke 1977). Precisamente, la Fig. 1 (a)
muestra que θ depende de la distancia entre estas zonas. Por lo tanto,
para un material débilmente correlacionado, la distancia de correlación θ
es menor, mientras que para materiales altamente correlacionados, el valor de θ
aumenta.
Una vez que las variables las estadísticas
(μ, σ, θ) de una propiedad de un tipo de suelo son
conocidas, una simulación numérica del campo de distribución de esta propiedad
puede ser generada utilizando el método de Subdivisión de Media Local (LAS)
(Fenton y Vanmarcke, 1990; Fenton 1990). Esta metodología genera medias locales
correlacionadas Z de acuerdo con una función de densidad de probabilidad
Gaussiana (con media cero y varianza unitaria) y una función de correlación
espacial ρ. Para un campo estocástico isotrópico, la función de correlación de
Gauss-Markov se define de acuerdo con la Ec. (6).
|
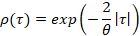
|
(6)
|
donde τ es un vector de desfase. El campo
estocástico así generado es entonces transformado de un campo Gaussiano para
otro definido por la función de densidad de probabilidad (pdf), utilizando las
expresiones de μ(z) y σ(z) de las Ecuaciones
(3)-(4), respectivamente. Para una distribución normal, la transformación se
define de la siguiente manera:
|
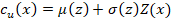
|
(7)
|
donde para problemas planos 2D, Z(x)
representa la media local de una celda de un campo estocástico con centroide en
x = (x, z) T. El método LAS en su versión actual
utiliza celdas cuadradas para generar el campo estocástico, esto significa que
el proceso de subdivisión se realiza a partir de un dominio externo cuadrado
pasando por una discretización sucesiva hasta llegar a una versión final,
formada por varias celdas cuadradas menores como se muestra en la Fig. 2. Cada
una de estas celdas está asociada a una única media local, la cual esta
correlacionada con las propiedades de las celdas adyacentes.
Para un grupo de datos estadísticos (μ,
σ, θ), existe un número infinito de campos estocásticos posibles
a ser generados. Aunque estadísticamente similares, cada campo representa una
distribución espacial diferente de la propiedad del material en cuestión.
d) Figura 2. Campos estocásticos bidimensionales de la variable X
generados con LAS, donde D representa la dimensión del dominio. Fuente.
Elaboración propia.
Por lo tanto, un análisis estocástico implica
una serie de análisis numéricos con MEF, las cuales son llamadas de
simulaciones y que están inmersas dentro del análisis de Montecarlo. Los
resultados obtenidos de las simulaciones conllevan a un análisis de
confiabilidad o riesgo, más que a la determinación de un único factor de
seguridad. Es decir, los resultados se expresan como funciones de densidad de
probabilidad (pdf), permitiendo establecer la probabilidad de falla de una
estructura en situaciones de colapso o en la obtención del valor más probable
de una variable de interés como ocurre en el cálculo del asentamiento de una
zapata. Cuanto mayor es el número de simulaciones más confiable es el resultado
obtenido, sin embargo, en la práctica no es posible realizar infinitos análisis
numéricos por diferentes razones. Por ejemplo, un número grande de simulaciones
conllevará a una demanda considerable de tiempo de cómputo, hecho que todavía
puede ser agravado a través de la utilización de una malla de EF bastante
refinada. De esta manera, es deseable establecer un número mínimo de
simulaciones a fin de obtener resultados confiables, estables y asegurar un
tiempo de cómputo adecuado.
Algoritmo
RFEM
Los parámetros estadísticos μ, σ, θ de
una variable de estado (por ejemplo, la resistencia no drenada al corte de un
suelo) pueden ser considerados a ser definidos a nivel puntual. Sin embargo,
las estadísticas a ese nivel de resolución son obviamente imposibles de medir
en la práctica, esto genera entonces incertidumbres asociadas con la
variabilidad del suelo. Lo anterior puede ser corregido utilizando una media
local que lleve en consideración el tamaño de la muestra, en este contexto el
método LAS actúa, mediante la generación de campos estocásticos para las
propiedades de interés del suelo. LAS está acoplado al MEF y al método MC, para
así definir el método RFEM. Es decir, a cada elemento o celda generada se le
atribuye un único valor estocástico de la propiedad, la cual permanece
constante en el dominio de la celda. De esta manera, la muestra del suelo es
representada por el tamaño de cada celda o elemento finito utilizado para
discretizar el dominio. Si la distribución del punto en cuestión es normal, el
proceso de subdivisión de media local aplicada al dominio en estudio, resulta
en una varianza reducida de la propiedad del material, pero con su media
inalterada. Sin embargo, en una distribución log-normal, tanto la media y la
desviación estándar se reducen durante el proceso, pues la media de una
distribución log-normal depende de la media y varianza de la distribución
normal asociada. Por lo tanto, una discretización grosera del problema con
mayores tamaños para los elementos, tendrá una mayor influencia del proceso de
media local. Estos ajustes en los puntos estadísticos son considerados dentro del
algoritmo del método RFEM.
RESULTADOS
Estudio
probabilístico de la estabilidad de un talud
En este caso, se estudia la probabilidad de
falla del talud mostrado en la Fig. 3 con la metodología RFEM. La malla de
elementos finitos utilizada en el modelo numérico también es mostrada en esta
figura. El talud presenta una pendiente 2: 1 con altura H=0,5 m y
profundidad D=0.75 m. Las condiciones de contorno son: base fija y
apoyos deslizantes en los contornos laterales. Cada elemento finito dentro de
la malla es un cuadrado de 0.05 m de lado. La discretización a lo largo de la
dirección horizontal está compuesta por 60 elementos (3 m) y a lo largo del
mayor lado vertical por 15 elementos (0.75 m). En total se utilizan 610
elementos finitos planos de ocho nodos con la hipótesis de deformación plana.
Es importante señalar que las dimensiones del talud son apenas representativas
y pueden corresponder a un modelo en escala. La distancia de correlación del
talud es parametrizada con Θ = θ / H, donde θ es la
distancia de correlación, todo esto con la finalidad de extender la validez de
los resultados para otras geometrías con igual valor de H/D.
e) 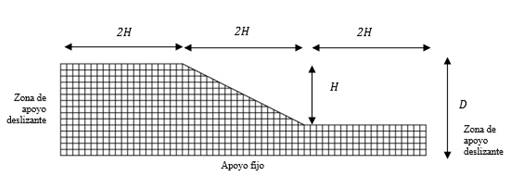
f)
Figura 3. Malla de elementos finitos utilizada.
Fuente. Elaboración propia.
La distancia de correlación se supone igual
en la dirección vertical y horizontal con θlnE = θlnγs
= θlncu = 1 m, donde θlnE, θlnγs
y θlncu son las distancias de correlación para el módulo de
elasticidad, peso específico y cohesión no drenada del suelo, respectivamente.
La media y la desviación estándar de cu (cohesión no drenada
del suelo) son μcu = 2 kPa y σcu = 0.5 kPa,
respectivamente (V=0.25), la media y la desviación estándar para γs
(peso específico del suelo) son μγs = 20 kN / m3 y
σγs = 2 kN / m3, respectivamente y la media y
desviación estándar para E (módulo de elasticidad) son μE
= 100000 kPa y σE = 50000 kPa, respectivamente. Otras
variables tales como el ángulo de fricción (∅ = 0o),
el ángulo de dilatancia (ψ = 0o) y el coeficiente de Poisson (v
= 0) son consideradas variables deterministas y, por lo tanto, constantes
durante el análisis numérico. La distancia de correlación parametrizada es Θ
= θ / H = 2, mientras que otras variables son: H/D
= 0.67, VE = σE / μE
= 0.5, Vcu = σcu / μcu =
0.25, Vγs = σγs / μγs =
0.1, μNs = μcu /(μγs H) =
0.2.
El nivel de correlación entre parámetros de
resistencia, tales como c y ∅ está pobremente documentado en
la literatura, además de no existir un consenso sobre sus valores entre los
investigadores. Sin embargo, valores en el rango de -0.24 a -0.70 ha sido
reportado en la literatura (Chok, 2008). El signo negativo se refiere a una
correlación totalmente negativa (osea un mayor valor de c corresponde
con un menor valor de ∅ y viceversa). Sin embargo, en este trabajo se supone una
correlación totalmente positiva para c y ∅ con un
coeficiente de correlación igual a 0.4. La correlación cruzada entre c y ∅
se considera utilizando la aproximación de descomposición de matriz de
covariancia, la cual está bien documentada en el trabajo de Fenton y Griffiths
(2008).
El presente análisis numérico implica la
aplicación de cargas de gravedad y el monitoreo de las tensiones en los puntos
de integración de cada elemento finito. Las fuerzas generadas por el peso
propio del depósito son calculadas por el procedimiento conocido en la
literatura inglesa como turn-on procedure (Smith et al., 2014). Este
procedimiento genera tensiones normales y de corte en los puntos de integración
dentro de la malla, los cuales serán posteriormente utilizadas para evaluar el
criterio de plastificación de Mohr-Coulomb, y de esta manera tener en cuenta la
no linealidad del material.
En primer lugar, un análisis determinista
es realizado considerando apenas las propiedades medias del suelo. De esta
manera, se puede obtener factores de seguridad reduciendo proporcionalmente los
valores de los parámetros de resistencia (cohesión y ángulo de fricción) hasta
encontrar la condición de falla del talud. Esta condición de falla se define numéricamente
cuando el algoritmo no converge después de 500 iteraciones (valor sugerido por
Fenton y Griffith, 2008). Los resultados obtenidos así, indicaron un factor de
seguridad de 1.30.
En una segunda fase, un análisis probabilístico
o estocástico es realizado considerando diferentes campos estocásticos para
cada una de las propiedades de interés del suelo. Los valores generados de esta
manera son transformados a un campo logarítmico (valores positivos) para ser
finalmente mapeados a la malla de elementos finitos (Fenton y Griffiths 2008).
Durante las simulaciones numéricas, el código de EF se ejecuta en modo de
detección falla. Es decir, las simulaciones que requieren más de 500
iteraciones para convergir o aquellas que no convergen caracterizan las
poblaciones de falla. Después de un número suficiente de simulaciones
(alrededor de 20000), la probabilidad de falla es determinada como la división
entre el número de simulaciones que indican falla y el número total de simulaciones.
El número de simulaciones necesarias dentro
de un análisis de Montecarlo para obtener una salida estable de los resultados
depende en gran medida de la variabilidad de los datos de entrada. La Fig. 4
muestra la probabilidad de falla para el presente talud como función del número
de simulaciones. Esta probabilidad es de aproximadamente de 0,18 y se
estabiliza para al menos 4000 simulaciones. Por lo tanto, se sugiere ese valor
mínimo para el análisis probabilístico de taludes con geometría similar a aquella
mostrada en la Fig. 3. Es importante destacar que cada punto de la curva
mostrada en la Fig. 4 corresponde a un análisis de MC con un número
predeterminado de simulaciones.
g) 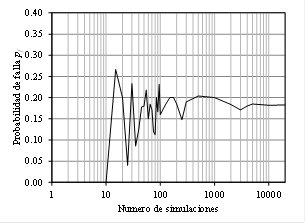
h) Figura 4. Estabilización de la probabilidad de falla con el número de
simulaciones. Fuente. Elaboración propia.
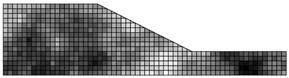
Como ilustración, en la Fig. 5 se presentan
en escala de grises los diferentes campos estocásticos generados para la
cohesión del suelo de acuerdo con la metodología LAS en diferentes
simulaciones. Las regiones más oscuras y claras representan mayores y menores
valores asignados para la cohesión, respectivamente. Después de la aplicación
del peso propio sobre el talud, las configuraciones deformadas obtenidas para
las mallas mostradas en la Fig. 5 son mostradas en la Fig. 6. Como se puede
apreciar, para el grupo de simulaciones mostradas, apenas la simulación No 1000
representa una condición de falla del talud después de no lograr convergir en
500 iteraciones. Otro detalle a destacar es que no necesariamente la superficie
de ruptura del talud es circular como se sugiere en otras metodologías (por
ejemplo, aquellas basadas en métodos de equilibrio limite o dovelas).
Precisamente esto constituye una ventaja de la presente metodología que no
supone un plano de falla a priori. En la Fig. 7 se muestran los campos de
velocidades de deformación del talud. Como se puede apreciar, la simulación No
1000 presenta inicialmente una superficie de falla casi circular la cual se
extiende hasta la superficie horizontal superior del talud.
|
i)
|
|
j)
Malla de EF correspondiente a la simulación No
1
k)
|
|
l)

|
|
m) Malla de EF correspondiente a la simulación No 100
n)
|
|
o) 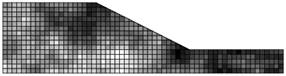
|
|
p) Malla de EF correspondiente a la simulación No 300
q)
|
|
r)

|
|
s)
Malla de EF correspondiente a la simulación No
500
t)
|
|
u) 
|
|
v) Malla de EF correspondiente a la simulación No 800
w)
|
|
x) 
|
|
y) Malla de EF correspondiente a la simulación No 1000
|
z)
Figura 5. Generación de campos estocásticos para la
cohesión. Fuente. Elaboración propia.
aa)
bb)
cc)
dd)
|
ee) 
|
|
ff) Configuración deformada correspondiente a la simulación No
1 (sin falla)
|
|
gg) 
|
|
hh) Configuración deformada correspondiente a la simulación No
100 (sin falla)
|
|
ii) 
|
|
jj) Configuración deformada correspondiente a la simulación No
300 (sin falla)
|
|
kk) 
|
|
ll) Configuración deformada correspondiente a la simulación No
500 (sin falla)
|
|
mm) 
|
|
nn) Configuración deformada correspondiente a la simulación No
800 (sin falla)
|
|
oo) 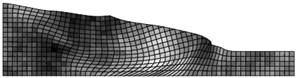
|
|
pp) Configuración deformada correspondiente a la simulación No
1000 (falla)
qq)
|
rr) Figura 6. Configuraciones deformadas del talud. Fuente. Elaboración
propia.
ss)
tt)
uu)
vv)
ww)
xx)
yy)
zz)
|
aaa)
|
|
bbb) Simulación
No 1
|
|
ccc) 
|
|
ddd) Simulación
No 100
|
|
eee) 
|
|
fff) Simulación No 300
|
|
ggg) 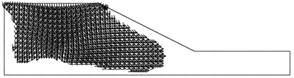
|
|
hhh) Simulación
No 500
|
|
iii) 
|
|
jjj) Simulación No 800
|
|
kkk) 
|
|
lll) Simulación No 1000 (falla)
mmm)
|
nnn) Figura 7.
Campo de velocidad de deformación. Fuente. Elaboración propia.
ooo)
ppp)
qqq)
Estudio
probabilístico de asentamientos producidos por una zapata rígida en el suelo
reformable.
Como segundo ejemplo, se realiza un estudio
probabilístico para el cálculo del asentamiento producido por la carga transmitida
por una zapata cuadrada rígida apoyada en un suelo deformable. La diferencia
con el ejemplo anterior, radica en la simulación numérica tridimensional del
problema. El módulo de elasticidad del suelo es la única variable aleatoria a
considerar, la cual será modelada mediante un campo estocástico tridimensional,
otras propiedades se consideran deterministas. El suelo se supone isotrópico
elástico con una estructura de correlación igual en la dirección vertical
cuanto en la dirección horizontal apenas por simplicidad. Sin embargo, se sabe
que existe una mayor correlación en la dirección horizontal debido a la
historia estratigráfica del suelo. La zapata está apoyada sobre una capa de
suelo deformable, y ésta su vez se apoya en una capa rígida (condición de apoyo
fijo en la base de la malla de elementos finitos) como se muestra en la Fig. 8.
El depósito del suelo es discretizado utilizando elementos hexahedricos de ocho
nudos, 64 elementos en cada dirección horizontal y 32 elementos en la dirección
vertical, totalizando 131072 elementos finitos.
Cada elemento es cubico con 0.15 m de lado,
definiendo un depósito con dimensiones en el plano horizontal (XY) de 9.6 m x
9.6 m y una profundidad de 4.8 m. Se observa que las unidades de distancia son arbitrarias
desde que se utilicen unidades consistentes de presión y fuerza. La carga de
servicio aplicada en cada nudo de la malla en la región bajo la zapata es de
1200 kN (Ver Fig. 8).
rrr) 
sss) Figura
8. Malla de elementos finitos del sistema suelo-zapata y valor de la carga
aplicada en kN. Fuente. Elaboración propia.
El análisis de elementos finitos utiliza un
solucionador de sistema de ecuaciones del tipo gradiente conjugado con
pre-condicionador lo que evita el montaje de la matriz de rigidez del sistema.
Las caras verticales de la malla están restringidas para moverse
horizontalmente, pero son libres de desplazarse verticalmente, mientras que los
nudos de la base se fijan en todas las direcciones simulando una condición
rígida. Se supone que la zapata es rígida (sin rotación) y está adherida al
suelo elástico de cimentación (sin deslizamiento). El asentamiento depende de
la magnitud de la carga aplicada y, por lo tanto, los resultados se pueden
expresar de forma paramétrica a fin de extender su aplicabilidad a otros
sistemas suelo-zapata con diferentes dimensiones, pero con relaciones de B/H
equivalentes, donde B es ancho de la zapata y H es la espesura
del depósito de suelo. Por ejemplo, el asentamiento de una zapata cuadrada de
dimensiones B= 4.0 m apoyada en una capa de suelo de espesor H'=20
m con P'=1000 kN y módulo de elasticidad E'=60 kN/m2
corresponde a 5/6 veces el asentamiento de una zapata de ancho B'=0.2 m
apoyada en una capa de suelo de espesor H=1 m con P=1 kN y módulo
elástico E=1 kN/m2. El factor de escala del primero para el
segundo sistema se define por el factor (P'/P)(E/E')(B/B')
siempre que B'/H'= B/H. Si B/H no es constante, otro
análisis determinista debe ser realizado a fin de determinar el nuevo factor de
escala. En el presente caso, se utilizaron los siguientes valores: B=1.8
m, H=4.8 m, θlnE = 1 m, μE = 20000
kPa, σE = 10000 kPa, B/H = 0.375 y σE/μE
= 0.5.
El suelo tiene dos propiedades de interés,
el módulo de elasticidad E(x) y el coeficiente de Poisson v(x),
los cuales dependen de la posición espacial x. En este estudio se
considerará apenas la aleatoriedad del módulo de elasticidad. El coeficiente de
Poisson presenta una variabilidad de segunda importancia según Fenton y
Griffiths (2008). La Fig. 9 muestra el campo estocástico tridimensional
generado para el módulo de elasticidad en una simulación típica. Para este
propósito, el algoritmo tridimensional del proceso LAS es utilizado. Las
rutinas de cómputo para este caso son también encontradas en el trabajo de Fenton
y Griffith (2008). Por lo tanto, para mayores detalles sobre el algoritmo
numérico y el código fuente, el lector es direccionado para dicha referencia.
En primer lugar, se realizan varios
análisis de Montecarlo con diferentes números de simulaciones hasta llegar a un
valor máximo de 5000 simulaciones. En la Fig. 10 se muestra la variación del
asentamiento máximo bajo la zapata conforme el número de simulaciones aumenta.
Como se puede observar, el valor del asentamiento se estabiliza aproximadamente
después de 500 simulaciones. De otra manera, en la Fig. 11 se muestra la
variación de la desviación estándar del asentamiento con el número de
simulaciones, es decir, en cada ejecución de un ciclo de Montecarlo, se calcula
la media y desviación estándar de esta variable. Se puede observar que la
desviación estándar se estabiliza también después de 500 simulaciones. Por lo
tanto, se sugiere considerar al menos 500 simulaciones para el análisis
probabilístico de este tipo de problemas.
Finalmente, en la Fig. 12 se muestra el
histograma correspondiente al asentamiento máximo producido bajo la zapata
obtenido para un análisis de MC con 5000 simulaciones. Se puede observar que la
tendencia del asentamiento es seguir la forma de una distribución normal o
log-normal. El asentamiento con valor igual a 1.957 cm tiene una frecuencia de
500 veces, resultando ser el valor más probable. Es importante destacar que
varias normas de cimentaciones limitan el asentamiento máximo diferencial en
servicio alrededor de 2.5 cm.
ttt) 
uuu) Figura 9:
Campo estocástico para el módulo de elasticidad del suelo generado con la
versión tridimensional del método LAS. Fuente: Elaboración propia.
vvv)
www)
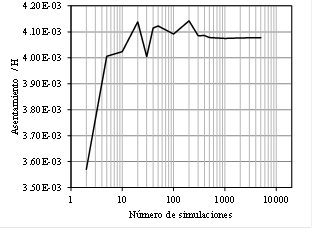
xxx) Figura 10.
Variación del asentamiento máximo con el número de simulaciones. Fuente.
Elaboración propia.
yyy)
zzz) 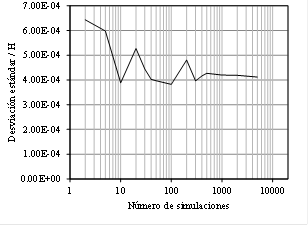
aaaa)
Figura 11: Variación de la desviación estándar del
asentamiento máximo con el número de simulaciones. Fuente. Elaboración propia.
bbbb)
cccc)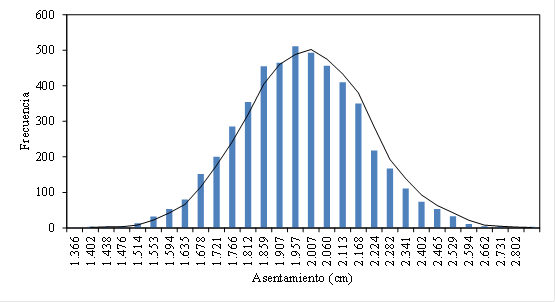
dddd)
Figura 12. Histograma de asentamientos después de
5000 simulaciones. Fuente. Elaboración propia.
CONCLUSIONES
• La eficiencia del modelo numérico en el
cálculo de probabilidades de falla o determinación de asentamientos probables
está asociada al esfuerzo computacional de un análisis de Montecarlo, la cual a
su vez depende del número de simulaciones. Cuanto mayor es el número de
simulaciones mayor será la confiabilidad en los resultados obtenidos, aunque
esto también estaría asociado a un incremento en el tiempo de cómputo, llegando
a ser prohibitivo en algunos casos, principalmente cuando son utilizados
computadores personales para la simulación. De esta manera, es deseable definir
un número de simulaciones mínimo que consiga satisfacer simultáneamente la estabilidad
de los resultados con el menor esfuerzo de cómputo. Para el ejemplo del talud,
la probabilidad de falla por peso propio fue de 0.18, valor que se estabiliza
después de 4000 simulaciones. Ya en el caso del cálculo del asentamiento de una
zapata rígida apoyada en un depósito de suelo deformable, el valor más probable
esta alrededor de 1.96 cm después de 500 simulaciones. Como una primera
tentativa para análisis estocásticos de estos problemas se sugiere utilizar
dichos valores.
• El análisis determinista del talud
sugiere un factor de seguridad alrededor de 1.3 en condiciones de peso propio.
Esto significa que la probabilidad de falla asociada seria cero, pues el factor
de seguridad es mayor que uno. Contrariamente, el análisis estocástico predice
una probabilidad de falla igual a 0.18 para el mismo talud. Esto muestra la
importancia de realizar un análisis que lleve en consideración las
incertidumbres de los materiales. Queda pendiente la extensión del presente
estudio para la consideración de las incertidumbres asociadas a las cargas
aplicadas en el sistema.
• La parte más compleja del algoritmo
RFEM corresponde al procedimiento LAS para la generación del campo estocástico
de la variable aleatoria de interés. La metodología LAS utilizada aquí se
mostró robusta numéricamente en lo que se refiere a tiempos de cómputo para un
computador personal. Las rutinas y programas obtenidos del trabajo de Fenton y
Griffiths (2008) pueden ser modificados o incluidos directamente en programas
de EF para estudios probabilísticos de problemas de concreto armado y de
interacción suelo-estructura. El primer autor ha trabajado en estas áreas
(Tamayo y Awruch 2016a,b) y está dentro de los próximos planes incluir la
metodología LAS en este tipo de problemas.
• La distancia de correlación es un
parámetro de difícil de determinar en la práctica, pudiendo variar inclusive
desde varios metros hasta kilómetros. En el abordaje de problemas de geotecnia
se sugiere estudiar el efecto de este parámetro en la respuesta probabilística
del sistema.
• La generación de campos estocásticos
involucra actualmente la definición de un dominio paralelepípedo o rectangular,
los cuales son representados por elementos cúbicos y rectángulos para el caso
tridimensional y bidimensional, respectivamente. El estudio de problemas que
involucran dominios curvos (reactores nucleares en estructuras de concreto
armado, depósitos, etc.) requiere el establecimiento de una regla de mapeo
adicional que permita convertir un dominio curvo en uno rectangular. Esta es
una tarea a desarrollar en futuras pesquisas.
REFERENCIAS
Bari, W. Modeling of ground improvement by
vertical drains inhighly variable soils, PhD thesis. Curtin University,
Western. 2012.
Bressani, L.A., COSTA, E.a. Probabilistic
evaluation of the stability of a slope colluvionar of basalt (In Portuguese),
IV Cobrae-Conferencia Brasileira sobre Estabilidade de Encostas, COBRAE,
Salvador, BA, Brazil, Vol. 4, p. 699-709, 2005.
CHOK, Y. Modelling the effects of soil variability and
vegetation on the stability of natural slopes, 2008. PhD thesis. School of
Civil, Environmental and Mining Engineering, The Universityof Adelaida.
Cavalcante, S.P.P.C., Vieira, V.P.P.B., Coutinho, R.Q.
Stability risk analysis of downstream slope of an operating dam (In
Portuguese), IV COBRAE-Conferencia Brasileira sobre Estabilidade de Encostas,
COBRAE, Salvador, BA, Brazil, Vol. 4, p. 515-530, 2005.
Fenton, G.A. Simulation and analysis of random fields
generators, 1990. PhD thesis. Princeton University, USA.
Fenton, G.A., Griffiths, D.V. Risk “Assessment in
Geotechnical Engineering”, 1st ed., USA: John Wiley and Sons, 2008.
Fenton, G.E., Vanmarcke, E. Simulation of random fields via
local average subdivision. Journal of Engineering Mechanics, v. 116, p.
1733-1749, 1990.
Lamus, Avelino Amado; Martínez, Edgar Hernán; Maldonado,
Esperanza. Estimación del daño sísmico para puentes de varios
vanos a partir de los modelos de Park y del ATC - 6.2. Revista
UIS Ingenierías, [S.l.], v. 2, n. 1, ene. 2012. ISSN 2145-8456.
Lumb, P. The variability of natural soils. Canadian
Geotechnical Journal, v. 3, p. 74-97, 1966.
Paiboon, J. Numerical analysis of homogenization using
random finite element method, 2013. PhD thesis. Colorado State University,
Colorado.
Smith, I. M., Griffiths, D.V., Margetts, L. Programming the
finite element. John Wiley and Sons Ltd, United Kingdom, 2014.
tamayo, j.p.l., awruch, a.m. On the validation of a
numerical model for the analysis of soil-structure interaction problems. Latin
American Journal of Solids and Structures, v. 13, n. 8, Jul – Dic, 2017. ISSN
1679-7825.
tamayo, j.p.l., awruch, a.m. Numerical simulation of
reinforced concrete nuclear containment under extreme loads. Structural
Engineering and Mechanics, v. 58, n. 5, 2016b. ISSN 1225-4568.
Vanmarcke, E. H. Random fields: analysis and synthesis. The
MIT press, Cambridge, Massachusetts, USA, 1983.
Vanmarcke, E. H. Probabilistic modelling of soil profiles.
Journal of Geotechnical Engineering Division, v. 103, p. 1227-1246, 1977.
, de esta propiedad en el análisis numérico o algún otro valor
característico sugerido por alguna norma de diseño. Sin embargo, en un proyecto
estocástico todas las propiedades de los materiales o por lo menos las más
importantes deben ser representadas a través de su media y desviación estándar
como se ilustra en la Fig. 1(b). En este último caso, la variabilidad de las
propiedades es expresada en términos de las funciones de densidad de
probabilidad (pdf), las cuales son precisamente caracterizadas por la media μ y
una desviación estándar normalizada, σ. Estas consideraciones definen el
llamado coeficiente de variación V mostrado en la Ec.1.
de un depósito de suelo. Por ejemplo, Lumb (1966) consideró una
tendencia lineal para una arcilla no drenada de la siguiente manera:
es la resistencia al corte no drenada y:
siendo una variable aleatoria normalizada con media cero y
desviación estándar unitaria, la cual varía de acuerdo con el tipo de función
de densidad de probabilidad seleccionada. Para una distribución normal, esta
función se define por la Ec. 5. Donde
,
y
en las ecuaciones 3 y 4 representan parámetros que definen la
variación de la media y desviación estándar, respectivamente, de la propiedad
en cuestión con la profundidad del suelo.