Análisis de sensibilidad y de estabilidad numérica en
el cálculo de factores de intensidad de tensiones en un caso de mecánica de
fractura
Analysis of
sensitivity and numerical stability in the calculation of factors of tension
intensity in a case of fracture mechanics
Wilson
Rodríguez-Calderón1, Rosangel Rojas-Aguero 2, José Yépez-Aguirre 3, Myriam Pallares-Muñoz 4
1Programa de Ingeniería Civil, Universidad Cooperativa de Colombia,
Colombia. Email: wilroca50@hotmail.com
Universidad Federal de Rio Grande del Sur, Porto Alegre, Brasil. Email:
rosangelrojasa@hotmail.com
Universidad Federal de Rio Grande del Sur,
Porto Alegre, Brasil. Email: chepel2@hotmail.com
4 Programa de
Ingeniería Civil, Universidad Surcolombiana, Neiva, Colombia. Email:
myriam.pallares@usco.edu.co
RESUMEN
El artículo aborda el cálculo de factores de
intensidad de tensiones en un caso de mecánica de fractura en placas de acero
bajo configuración de carga uniforme. Se explora la sensibilidad del factor de
primer modo de intensidad de tensiones KI respecto a las relaciones a/w, a/h,
h/w (a: tamaño de fractura inicial, w: ancho de placa, h: distancia vertical
entre la fractura y la línea de carga). Se realizan comparaciones de los
resultados obtenidos por diferentes metodologías como la analítica obtenida de
la literatura, el método de colocación del contorno implementado en el software
libre MAXIMA y el método de elementos finitos implementado a través de un modelo
en ANSYS. Dado que, el método de colocación del contorno incorpora una solución
generalizada por mínimos cuadrados, es posible observar algunos problemas de
inestabilidad numérica asociados principalmente a casos en los que el tamaño de
la fractura inicial es considerable respecto al ancho de la placa cargada. Los
aportes más destacados se dan respecto al análisis de sensibilidad particular
del caso, el análisis de problemas de inestabilidad numérica en situaciones
específicas de cálculo de KI, implementaciones de códigos en software libre
como MAXIMA e implementación de modelos de elementos finitos en ANSYS usando
elementos Quarter Point. Los resultados obtenidos se reportan mediante
comparaciones numéricas y gráficas del comportamiento del factor KI para las
diferentes relaciones estudiadas, bajo las diferentes metodologías. El articulo
concluye sobre cuáles son las relaciones significativas en la sensibilidad del
factor de intensidad de tensiones KI y el origen de los problemas de
inestabilidad numérica del método de colocación mediante el estudio paramétrico
asociado al número de condición del sistema de la matriz global del mismo
método.
PALABRAS
CLAVE: Análisis de
sensibilidad, ANSYS, Método de colocación del contorno, MAXIMA, Elementos
finitos, Fractura.
ABSTRACT
The article studies the calculation of stress intensity
factors in a case of fracture mechanics in steel plates under uniform load
configuration. The sensitivity of the first mode factor of stress intensity KI with respect to the
relationships a/w, a/h, h/w (a: initial fracture size, w: plate width, h:
vertical distance between fracture and the loading line) is explored. We
perform comparisons of the results obtained by different methodologies such as
the analytical obtained from the literature, the method of placement of the
contour implemented in the free software MAXIMA and the finite element method
implemented through a model in ANSYS. Since the method of positioning the
contour incorporates a generalized least squares solution, we could observe
some problems of numerical instability associated mainly to cases in which the
size of the initial fracture is considerable with respect to the width of the
loaded plate. The most relevant contributions are given regarding the
particular sensitivity analysis of the case, the analysis of problems of
numerical instability in specific situations of KI calculation, implementations of free software codes
such as MAXIMA and implementation of finite element models in ANSYS using
Quarter Elements Point. The results obtained are reported by numerical and
graphical comparisons of the behavior of the KI
factor for the different relationships studied under different methodologies.
The article concludes on what are the significant relations in the sensitivity
of the stress intensity factor KI
and the origin of the problems of numerical instability of the placement method
by the parametric study associated to the condition number of the system of the
global matrix of the same method.
KEYWORDS: Sensibility analysis, ANSYS,
Method of placement of the contour, MAXIMA, Finite
elements, Fracture mechanics.
INTRODUCCIÓN
El cálculo del factor de intensidad de
tensiones KI (modo 1 o modo de apertura) tiene importancia práctica para la
determinación de la posibilidad inminente de fractura de una pieza o elemento
estructural, así como en la determinación de variables asociadas al cálculo de
esfuerzos de fractura y de parámetros de energía de fractura. En el artículo se
aborda el estudio de un problema clásico de una placa con grieta de tamaño a
bajo carga uniforme aprovechando que particularmente existe disponibilidad de
soluciones teóricas para realizar comparaciones frente a opciones numéricas. La
figura 1 muestra el problema de fractura parametrizado donde w es el ancho de la placa, h es la distancia
vertical entre la grieta y la línea de carga, p el valor de la carga
distribuida por unidad de área y a el tamaño de la grieta.
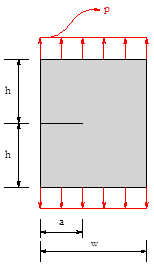
Figura 1. Caso de fractura en modo de apertura
parametrizado. Fuente. Elaboración propia.
Calculo
teórico del factor de intensidad de tensiones modo i para el caso de carga
uniforme
En la literatura pueden encontrase diferentes
fórmulas más o menos calibradas para el cálculo del factor de intensidad de
tensiones KI, a
continuación, se muestra la fórmula empleada en el análisis reportado en este
artículo:
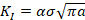 (1)
(1)
Donde a es un factor de corrección de
geométrica cuya expresión es:
 (2)
(2)
Calculo
numérico del factor de intensidad de tensiones KI para
el caso de carga uniforme por el método de colocación del contorno
William (1957, [1]) encontró una solución general
para el campo de tensiones general alrededor de una grieta (ver figura 2)
empleando las denominadas funciones de Airy así:
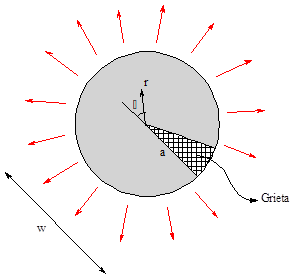
Figura 2. Dominio alrededor de una grieta.
Fuente. Elaboración propia.
Aplicando las ecuaciones (3), (4) y (5) a
puntos igualmente espaciados alrededor del contorno de la grieta y aprovechando
la simetría es posible obtener un sistema lineal de ecuaciones. Debe tenerse en
cuenta que las condiciones de contorno del problema son conocidas. En la figura
3 se ilustra el proceso de discretización y las condiciones de contorno
aplicadas.
 (a)
(a)
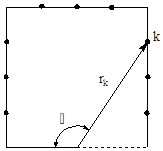 (b)
(b)
Figura 3. Problema
de fractura bajo carga uniforme. (a) Condiciones de contorno (b) Discretización
del contorno en el método de colocación del contorno k=1,n (n=9 para la
figura). Fuente. Elaboración propia.
A continuación, se ilustra el planteamiento
matemático del método de colocación del contorno (Gross et al, 1964), teniendo
en cuenta que los subíndices de s indican el punto en cuestión y las tensiones s pueden
ser para el caso tensiones xx, yy o xy aplicadas punto a punto por la
imposición de las condiciones de contorno y las funciones fj
y fm corresponden a las funciones que acompañan
a los coeficientes Aj, Bm respectivamente, dentro de la expresión correspondiente para la tensión
evaluada mediante las ecuaciones generales 3, 4 y 5. Los valores límite J y M para
el desarrollo de las series pueden ser determinados en la práctica por la
calibración del número de términos necesario para la convergencia de la serie a
valores constantes. De esta manera la formulación sería:
Donde:
sn ® Tensiones xx, yy o xy
conocidas en el contorno.
Aj,Bm ® Coeficientes
de desarrollo de las series a ser determinados.
fj,gm ® Funciones de William.
Del proceso de las ecuaciones (6) resulta un
sistema lineal de ecuaciones no cuadrado así:
|
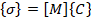
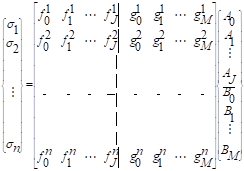
|
(7)
|
|
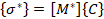 (8) (8)
Donde:
{s*} =[M]T{s}
[M*]=[M]T[M]
|
(8)
|
El sistema (8) puede ser resuelto por algún
método de factorización o por métodos iterativos. En el caso de este artículo
se empleó la factorización LU. Resuelto el sistema y determinado el vector C,
es posible calcular KI
como KI = A0 (2pw)0.5
Calculo
numérico del factor de intensidad de tensiones KI para el caso de carga uniforme por
el método de elementos finitos
El artículo no aborda toda la formulación de
elementos finitos del problema de fractura, más bien se hace énfasis en detalles
particulares importantes para la modelación del fenómeno y para el cálculo del
factor de intensidad de tensiones. Respecto a los elementos finitos es
importante anotar que es común emplear elementos finitos especiales alrededor
de la punta de la grieta, estos elementos se denominan elementos quarter point
y tienen la cualidad de capturar de manera muy precisa el campo de
desplazamientos y de tensiones en la cercanía de la punta de la grieta donde
los gradientes de tensiones son realmente altos.
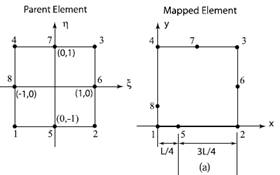
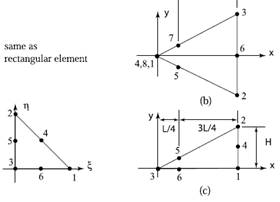
Figura 4. Elementos quarter-point en
coordenadas naturales (parent element) y coordenadas reales (mapped element)
(a) Elemento cuadrilátero de 8 nodos (b) Elemento triangular por colapso de los
nodos 4,8 y 1. (c) Elemento triangular natural (recomendado para problemas
lineales). Fuente. Fracture mechanics, Alan T. Zehnder, pag. 91.
Para el cálculo del factor de intensidad de
tensiones puede evaluarse este en dos puntos cercanos a la punta de la grieta,
que comúnmente son los dos nodos del elemento quarter point sobre la grieta.
Teniendo esto es posible extrapolar linealmente a la punta de la grieta y
calcular de este modo el factor de intensidad de tensiones correcto. La fórmula
empleada para evaluar el factor de intensidad de tensiones en los nodos
mencionados es:
|
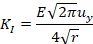
|
(9)
|
MÉTODOS
Calibración
del método de colocación del contorno para el caso de carga uniforme usando el
cas libre MAXIMA
Para ilustrar un poco sobre el sistema de algebra
computacional CAS usado, puede decirse que MAXIMA es un sistema para la
manipulación de expresiones simbólicas y numéricas, que produce resultados de
alta precisión usando fracciones exactas, números enteros de precisión
arbitraria y números de coma flotante con precisión variable. Por otra parte,
puede graficar funciones y datos en dos y tres dimensiones. Dado que es un
programa libre puede ser compilado en varios sistemas operativos como Windows,
Linux y MacOS X. MAXIMA es un descendiente de Macsyma, un sistema de álgebra
computacional desarrollado a finales de 1960 en el Instituto Tecnológico de
Massachusetts (MIT). Este es el único sistema basado en ese programa que está
todavía disponible públicamente y con una comunidad activa de usuarios, gracias
a la naturaleza del software abierto. Macsyma fue revolucionario en su tiempo y
muchos sistemas posteriores, como Maple y Mathematica, se inspiraron en él. La
rama MAXIMA de Macsyma fue mantenida por William Schelter desde 1982 hasta su
muerte en 2001. En 1998 él obtuvo permiso para liberar el código fuente bajo la
licencia de software libre GPL. Entrando al tema de la calibración, dado que,
el método de colocación del contorno implica una discretización de la frontera
del dominio y un desarrollo truncado de las series, se requiere conocer el
número de coeficientes y el número de puntos de análisis necesarios para llegar
a un valor estable en el cálculo del factor de intensidad de tensiones. Para la
implementación se realizó un desarrollo de un macro y un archivo de
instrucciones bajo el lenguaje propio de MAXIMA, debido a que se requiere
realizar ciclos de cálculo que se desarrollan mediante la llamada continua al
macro desarrollado en MAXIMA, este se encarga de calcular el factor de
intensidad de tensiones para cada uno de los llamados y así poder generar una
curva de convergencia o de calibración del método. MAXIMA posee ventajas
respecto a su capacidad simbólica, su capacidad gráfica y la riqueza de
comandos disponibles para la generación de macros adaptados a las necesidades
específicas de un problema. Para la calibración primero se realizan ciclos de
cálculo incrementando el número de coeficientes presentes en la formulación
(J,M) desde 5 hasta 50 con paso de 5 (ver figura 5). Una vez encontrada la cantidad
eficiente de coeficientes se realiza una segunda calibración del número de
puntos necesario para la discretización que es manejado por una formula interna
que es 3*(nd-1) donde nd varia de 5 a 30 con paso de 5 y este representa el
número de divisiones de cada línea que por facilidad se maneja igual para las
tres líneas del modelo, el valor de 30 divisiones puede ser incrementado solo
que con algunas pruebas es posible determinar que 30 es un número de divisiones
razonable para resultados satisfactorios (ver figura 6). El macro de máxima
desarrollado calcula además el número de condición de la matriz M* para conocer
un índice del condicionamiento de la matriz y de la posible afectación de los
resultados si la matriz resultante posee un numero de condición demasiado alto.
La figura 5 muestra el proceso iterativo de un modelo donde a=50 mm, h=100mm,
w=100 mm, p=1 MPa, nd=30, J=M= [5…50] con paso de 5. En esta figura puede verse
que un número razonable para desarrollar las series es J=M=30.
La figura 6 muestra los resultados obtenidos
dejando fijo el número de coeficientes ya determinado e incrementando el número
de puntos como ya se explicó.
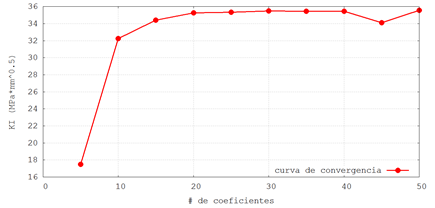
Figura 5. Curva de convergencia para elegir el
número eficiente de coeficientes a tener en cuenta para el desarrollo de las
series de la solución de William. Fuente. Elaboración propia.
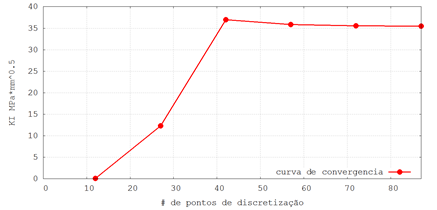
Figura 6. Curva de convergencia para determinar
una solución estable del factor de intensidad de tensiones. Fuente. Elaboración
propia.
RESULTADOS
Modelo
de elementos finitos para el cálculo de factor de intensidad de tensiones para
el caso de carga uniforme usando ANSYS
Los datos básicos usados para el modelo
mostrado a continuación son: a=10 mm, h=100mm, w=100 mm, p=1 MPa, E=200 GPa (modulo
elástico), n=0.3 (coeficiente de Poisson), Espesor = 1mm. La figura 7 muestra las
condiciones de carga (1), las condiciones de apoyo del modelo (2) y los
detalles de los nodos de los elementos quarter point alrededor de la punta de
la grieta (3). La malla es no estructurada, el elemento finito usado es el
PLANE183, bajo la opción de esfuerzo plano con constante real de espesor
especificado, por último, se realizaron test de malla, para una densidad
razonable de elementos que capturen la solución de manera precisa.
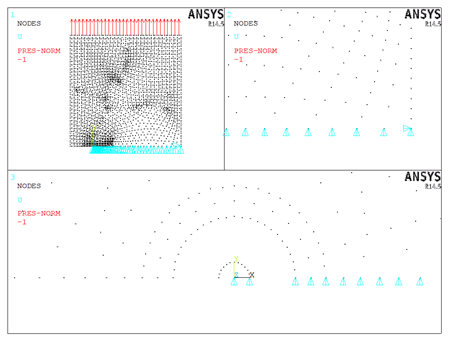
Figura 7. Condiciones de carga (1), condiciones
de apoyo del modelo (2) y detalles de los nodos de los elementos quarter point
alrededor de la punta de la grieta (3). Fuente: Elaboración propia.
La figura 8 muestra la deformada (3) e
isocontornos de desplazamiento vertical (2) y horizontal (1). Basado en los
resultados de la ventana 2 de la figura se realizan los cálculos como ya se
explicó anteriormente en el apartado 1.3 y usando como parte del proceso la
ecuación (9).
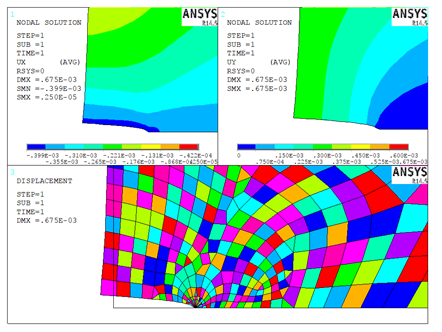
Figura 8. Postproceso de deformada (3) e
isocontornos de desplazamiento vertical (2) y horizontal (1). Fuente:
Elaboración propia.
La Figura 9 muestra los isocontornos de
tensiones normales xx (1), yy (2) y las tensiones de corte xy (3). Puede verse
concentraciones de tensiones en cada uno de los componentes de tensión.
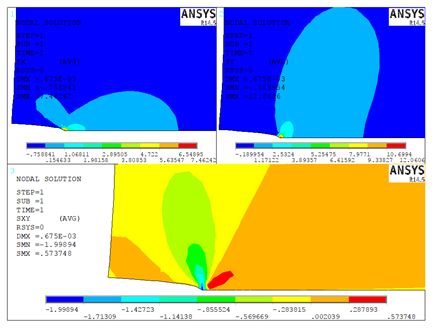
Figura 9. Isocontornos de tensiones normales xx
(1), yy (2) y las tensiones de corte xy (3). Fuente. Elaboración propia.
Análisis
de sensibilidad y de estabilidad numérica del cálculo del factor de intensidad
de tensiones para el caso de carga uniforme
En este apartado se explica el análisis de
sensibilidad del factor de primer modo de intensidad de tensiones KI respecto a las relaciones a/w, a/h,
h/w (a: tamaño de fractura inicial, w: ancho de placa, h: distancia vertical
entre la fractura y la línea de carga). La figura 9 muestra comparaciones de
los resultados obtenidos por vía analítica, usando el método de colocación del
contorno implementado en el software libre MAXIMA y el método de elementos
finitos implementado a través del modelo en ANSYS. Para la sensibilidad se
hacen barridos de cada una de las relaciones mencionadas y se calcula el factor
de intensidad de tensiones, lo que implica realizar varios análisis cambiando
el valor de los parámetros y para esto es útil el empleo de los modelos
numéricos y teóricos ya parametrizados e implementados en las diferentes
herramientas computacionales.
Dado que, el método de colocación del contorno
incorpora una solución generalizada por mínimos cuadrados, es posible observar
algunos problemas de inestabilidad numérica asociados principalmente a casos en
los que el tamaño de la fractura inicial es considerable respecto al ancho de
la placa cargada. Al respecto, puede verse que en la figura 10 que los valores
de KI evaluados en la
relación a/w de 0.8 y 0.9 se alejan de la solución analítica tanto en el modelo
de ANSYS, como en el método de colocación del contorno. Si se observa en el eje
secundario de la gráfica está el valor del número de condición de la matriz M*
del método de colocación y puede verse que en a/w de 0.8 y 0.9 se dan cambios
importantes en el condicionamiento de la matriz que afectan la lógica misma del
valor del factor de intensidad de tensiones que aumenta con el tamaño de la
grieta, indudablemente en esta zona los resultados no son confiables, en los
valores de a/w de 0.1 y 0.2 también hay números de condición un poco grandes,
sin embargo el cálculo de KI se mantiene dentro de valores correctos. En el valor de a/w de 0.5 se
da el menor número de condición y por esto se eligió este modelo para la
calibración adecuada del método de colocación en el problema.
Respecto a las diferencias de las curvas de
sensibilidad de a/w vs KI
analítico y de ANSYS, es posible que la formula analítica posea restricciones
para el cálculo de KI
cuando el tamaño de la grieta sea grande como en los valores a/w de 0.8 y 0.9,
para analizar esto se realizaron refinamientos de malla en ANSYS sin obtener
cambios significativos en KI. En la literatura algunas fórmulas advierten límites de aplicación en
grietas grandes, sin embargo, la formula usada no reporta nada al respecto. El
comportamiento de la curva de sensibilidad de a/w vs KI analítico sigue la lógica de incrementar el valor de KI con el incremento de a/w y quedaría
para la verificación experimental que pasa con KI en los valores de a/w de 0.8 y 0.9, en todo caso ANSYS supervalora a KI respecto a la solución analítica y
esto iría en favor de la seguridad.
Las sensibilidades de KI respecto a a/h y h/w no se encontraron en la literatura, no obstante,
los resultados ratifican que KI se mantiene prácticamente constante variando la relación h/w, luego KI no es sensible a esta relación, por
otra parte, respecto a a/h se encuentra algo de sensibilidad, pero no
comparable a la encontrada en a/w. Los incrementos realizados en a/h implican
un acercamiento de la carga a la grieta que conduce a un aumento del factor KI.
Finalmente, puede verse que los resultados
indican que la sensibilidad más importante se da respecto a la relación a/w y
explica la abundancia de soluciones analíticas para el cálculo de KI como función de la relación a/w. Se
advierten cuidados importantes a tener en cuenta cuando la grieta se hace
grande (a/w>0.8), ya que, pueden existir dudas sobre la certeza del cálculo
por lo que se recomienda usar en este caso un modelador de elementos finitos
(el cálculo por colocación infravalora KI cuando la grieta es grande).
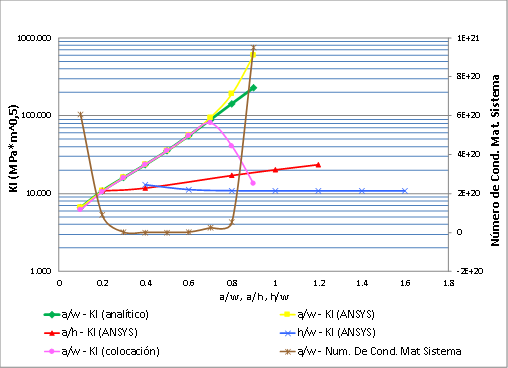
Figura 10. Curvas de sensibilidad y de
condicionamiento del cálculo del factor de intensidad de tensiones para el caso
de carga uniforme. Fuente. Autores.
CONCLUSIONES
El artículo concluye que la relación de mayor
sensibilidad para el factor de intensidad de tensiones es a/w, mientras que la
relación h/w prácticamente no presenta ninguna sensibilidad y la relación a/h
presenta una sensibilidad moderada. El origen de los problemas de inestabilidad
numérica del método de colocación se determinó mediante el estudio paramétrico
asociado al número de condición del sistema de la matriz global del mismo
método, encontrando que cuando la relación a/w toma valores iguales o superiores
a 0.8 el método entrega resultados errados. Respecto a las implementaciones, el
software libre MAXIMA representa una excelente alternativa para atacar
problemas de alta complejidad simbólica y numérica, ya que este cuenta con
funciones básicas y avanzadas para desarrollar macros de manera adaptada y
eficiente. Los modelos realizados con ANSYS muestran resultados muy
satisfactorios que colocan esta herramienta como un instrumento confiable para
modelar problemas de fractura bajo diferentes configuraciones de geometría.
REFERENCIAS
[1] Anderson, T. L. Fracture Mechanics: Fundamentals and
Applications. CRC Press, 2005. ISBN 0849316561.
[2] Barsoum, R. S. On The Use of Isoparametric Finite
Elements in Linear Fracture Mechanics. International Journal for Numerical
Methods in Engineering, V. 10, N. 1, P. 25-37, 1976. ISSN
1097-0207. 1976.
[3] Bittencourt, E. Mecânica Da Fratura E Do
Dano. UFRGS 2011.
[4] González, V.; Maravilla, E.; Tarancón, J.
“Descripción del crecimiento de grietas usando una aproximación geométrica
basada en level sets y fast marching method”. Revista uis ingenierías, [s.l.],
v. 16, n. 1, ene. 2017. ISSN 2145-8456. [En Línea] Disponible en: http://revistas.uis.edu.co/index.php/revistauisingenierias/article/view/6011.
[5] González. V.; Maravilla. E.; Tarancón, J.
“Comparación de esquemas de integración 3D para elementos enriquecidos en
XFEM”. Revista UIS Ingenierías, [s.l.], v. 15, n. 2, nov. 2016. ISSN 2145-8456.
[En Línea] Disponible en:
http://revistas.uis.edu.co/index.php/revistauisingenierias/article/view/7-16 https://doi.org/10.18273/revuin.v15n2-2016001.
[6] González, O.; Leal, j.; Reyes, J.
“Análisis de integridad estructural de tuberías de material compuesto para el
transporte de hidrocarburos por elementos finitos”. Revista UIS Ingenierías,
[S.l.], v. 15, n. 2, nov. 2016. ISSN 2145-8456. [En Línea] Dispónible en: http://revistas.uis.edu.co/index.php/revistauisingenierias/article/view/105-116.
https://doi.org/10.18273/revuin.v15n2-2016009.
[7] Gross, B.; Srawley, J. E.; Brown Jr, W. F.
Stress-Intensity Factors for A Single-Edge-Notch Tension Specimen by Boundary
Collocation of a Stress Function. DTIC Document. 1964
[8] Hibbitt, H. Some Properties of Singular Isoparametric
Elements. International Journal for Numerical Methods in Engineering, V. 11, N.
1, P. 180-184, 1977. ISSN 1097-0207. 1977.
[9] Hughes, T. J. The Finite Element Method: Linear Static
and Dynamic Finite Element Analysis. Courier Dover Publications, 2012. ISBN
0486135020.
[10] Ingraffea, A. R.; Manu, C. Stress‐Intensity Factor Computation
in Three Dimensions with Quarter‐Point
Elements. International Journal for Numerical Methods in Engineering, V. 15, N.
10, P. 1427-1445, 1980. ISSN 1097-0207.
[11] Peano, A.; Pasini, A. A Warning Against Misuse of
Quarter‐Point Elements.
International Journal for Numerical Methods in Engineering, V. 18, N. 2, P.
314-320, 1982. ISSN 1097-0207.
[12] Pin, T.; Pian, T. H. On The Convergence of the Finite
Element Method for Problems with Singularity. International Journal of Solids
and Structures, V. 9, N. 3, P. 313-321, 1973. ISSN 0020-7683.
[13] Quintero, Y. et al. “Optimización de
diseños de fractura hidráulica aplicando estudios geomecánicos”. Revista
fuentes, [s.l.], v. 8, n. 2, mayo 2011. ISSN 2145-8502. [En Línea] Disponible
en: http://revistas.uis.edu.co/index.php/revistafuentes/article/view/1626
[14] Zehnder, A. T. “Lecture Notes On Fracture Mechanics.
Available for Public Use at Cornell University” [En Línea] Disponible en:
http://Ecommons. Library. Cornell.
[15] Edu/Bitstream/1813/3075/6/Fracture_Notes_20
08.pdf, 2007.
(1)
(2)
(a)
(b)