Ubicación óptima de monitores de hundimientos de tensión en redes de distribución incorporando restricciones de localización de fallas de red

Optimal placement of voltage sag meters in distribution networks using fault location constraints

Edinson Cabezas-Jaimes¹, Jairo Blanco-Solano², Johann Farith Petit-Suárez³, Gabriel Ordóñez-Plata⁴

¹Electrificadora de Santander SA, Colombia. Email: edinson.cabezas@gmail.com

²Grupo de Investigación en Sistemas de Energía Eléctrica - GISEL, Escuela de Ingenierías Eléctrica, Electrónica y de Telecomunicaciones, Universidad Industrial de Santander, Colombia. Email: jairo.blanco@correo.uis.edu.co

³ Grupo de Investigación en Sistemas de Energía Eléctrica - GISEL, Escuela de Ingenierías Eléctrica, Electrónica y de Telecomunicaciones, Universidad Industrial de Santander, Colombia. Email: jfpetit@uis.edu.co

⁴Grupo de Investigación en Sistemas de Energía Eléctrica - GISEL, Escuela de Ingenierías Eléctrica, Electrónica y de Telecomunicaciones, Universidad Industrial de Santander, Colombia. Email: gaby@uis.edu.co

RESUMEN

En este trabajo se propone un nuevo método para la ubicación óptima de monitores de hundimientos de tensión, formulando un problema de optimización que incorpora: condiciones desbalanceadas de la red eléctrica; alimentadores trifásicos, bifásicos y monofásicos; la caracterización estadística de las impedancias de falla y restricciones de observabilidad derivadas de una técnica de localización relativa de fallas en la red. El principal aporte de este trabajo es la formulación de un nuevo problema de optimización donde los sistemas de monitorización pueden ser proyectados hacia la gestión avanzada de la actividad de distribución de energía eléctrica. El método propuesto es aplicado a una red de distribución real de 379 nodos de un operador de red de Colombia. La configuración óptima de los monitores es determinada y los resultados validan como un sistema de monitorización es optimizado considerando las características reales de las fallas de red en los sistemas de distribución. 

PALABRAS CLAVE: Calidad de potencia, Hundimientos de tensión, Fallas de red, Ubicación óptima, Monitorización inteligente. 

ABSTRACT

A new method is developed for optimal placement of voltage sag meters. It is based on a new optimization problem that includes: network unbalanced conditions; three-phase, two-phase and single-phase feeders; a statistical characterization of the fault impedances, and observability constraints derived from the fault relative location techniques. The main contribution is a new optimization problem formulation to guarantee that the monitoring system would be an advanced management tool in the power distribution. The proposed method is tested in a real 379-node distribution network of a Colombian network operator. Meters optimal configuration is obtained and the results show how a monitoring system may be optimized considering the real features of the network faults in distribution systems.

KEYWORDS: Power Quality, Voltage Sags, Network Faults, Optimal Placement, Smart Metering.

1. INTRODUCCIÓN

Los hundimientos de tensión y su creciente impacto en equipos y procesos han generado gran preocupación entre operadores de red y sus respectivos usuarios del servicio de energía eléctrica. Esta problemática impacta en todas las fronteras de conexión (transmisión – distribución, distribución – distribución, distribución – micro red y distribución – usuario final) y por ende la importancia demandada en su continuo estudio. El efecto de este tipo de perturbaciones ha conllevado a una continua búsqueda de estrategias para su identificación, clasificación, diagnóstico, evaluación y mitigación [1], [2]. Además, con la masificación de equipos electrónicos que cada día son más sensibles a estas perturbaciones, se han generado pérdidas económicas significativas en diferentes sectores productivos [3]. Estas pérdidas se asocian a las fallas de los mismos equipos y como consecuencia la interrupción de procesos y el consecuente deterioro en la elaboración de productos.

Uno de los principales retos en la actualidad es el diagnóstico y la localización de las fuentes generadoras de los hundimientos de tensión. Como respuesta a esta problemática, son implementados modernos sistemas de monitorización para medir y caracterizar el estado de las variaciones de tensión en los nodos de una red eléctrica. A su vez y de forma paralela, se presentan constantes y novedosos desarrollos en las tecnologías de medición inteligente y de comunicación, brindando nuevas posibilidades para la gestión avanzada de las redes de distribución [4].  No obstante, es claro que la instalación de monitores en cada nodo del sistema eléctrico no es económicamente viable, por lo cual surge el problema de ubicación óptima de estos monitores con funciones “smart”.

Existe en la literatura técnica un número importante de métodos que abordan este problema desde la perspectiva de optimización, destacándose los planteamientos basados en la Matriz de Observabilidad de Hundimientos de Tensión (MOHT) [3], [5]–[8]. Esta matriz, que puede ser denominada también como una matriz de sensado, es construida en condiciones específicas e idealizadas en un análisis de cortocircuito, tales como: fallas de red con impedancia cero, tensiones de pre-falla nominales, condiciones nominales y balanceadas de carga. Por lo tanto, estos aspectos pueden generar resultados imprecisos cuando los métodos de localización óptima son evaluados en condiciones reales de falla de las redes de distribución [9], [10].

El presente trabajo propone un método para la ubicación óptima de monitores de hundimientos de tensión que considera dentro de la formulación del problema de optimización las condiciones desbalanceadas de la red eléctrica, los alimentadores trifásicos, bifásicos y monofásicos, el modelado estadístico de las impedancias de falla, e incorpora restricciones de observabilidad derivadas de una técnica de localización relativa de fallas en la red [11].

El documento está organizado de la siguiente manera: En la sección 2 se describe brevemente algunas metodologías que utilizan la MOHT para formular el problema de ubicación óptima de los monitores. En la sección 3 se presenta el nuevo método de ubicación óptima incorporando las restricciones de localización relativa de fallas en la red. En la sección 4 se muestran los resultados obtenidos con la aplicación de la nueva metodología sobre una red de distribución real, de 13,2 kV y 379 nodos, de un operador de red en Colombia. Finalmente, en la sección 5 se presentan las conclusiones del trabajo.

2. UBICACIÓN ÓPTIMA DE MONITORES USANDO LA MOHT

Varios trabajos basados en la MOHT han sido propuestos en los últimos años para la solución al problema de ubicación óptima de monitores de hundimientos de tensión [3], [5]–[8]. El concepto de Área de Alcance del Monitor (AAM) es el más popular en la literatura técnica, cuyo principio es garantizar la obervabilidad de toda la red eléctrica ante cualquier hundimiento de tensión. En su construcción y modelado matemático usa el método de Locaciones de Falla (LF), que consiste en la segmentación de líneas, definiendo puntos de falla posibles tanto en líneas como en barras. Como criterio de optimalidad, se debe garantizar que todos los hundimientos de tensión deben ser observados o registrados al menos por un monitor para una falla dada y para un umbral de detección establecido [8], [9], [12]– [15].

 Este umbral es normalmente 0.9 p.u. La MOHT se puede ser representada de forma binaria, según las reglas matemáticas presentadas en (1). Su construcción es a partir de un análisis de cortocircuito, usando un software para tal fin como Neplan, Digsilent, Matlab o ATPEMTP. Por lo tanto, se realizan todos los tipos de fallas en la red y generalmente con impedancia de falla ₍𝑍_𝑓) igual a cero; de igual manera en todas las locaciones de falla definidas y finalmente las tensiones residuales (𝑉𝑟_𝑗) en barras se comparan con un umbral predeterminado µ.

 1, 𝑠𝑖 𝑉𝑟_𝑖𝑗 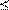 µ  

(𝑖,𝑗) = { 0, 𝑠𝑖 𝑉𝑟𝑖𝑗  µ                    (1)

En (1),  corresponde a la barra para la posible instalación del monitor, mientras 𝑖 es la locación de la falla simulada; finalmente,  µ es el umbral de detección. Adicionalmente, en (2) se define un vector de decisión, siendo 𝑥_𝑖 igual a 1 para indicar la instalación del monitor de hundimientos de tensión en la barra 𝑗. Un valor cero, indica la no instalación del monitor.

1, si se instala un monitor en la barra 𝑖

^{𝑥𝑖 = {}0, no se instala un monitor en la barra 𝑖   ⁽²⁾

Finalmente, se establece el problema de optimización para garantizar la observabilidad de los hundimientos de tensión y cuyo objetivo es minimizar el costo de instalación del conjunto de monitores necesarios, como se muestra en (3).

𝑁

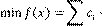𝑥_𝑖

𝑖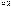

(3)

𝑁

sujeto a: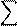𝐀𝐀𝐌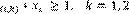 , … , 𝑁_𝑝𝑓

𝑖

En (3), 𝑐_𝑖 es el costo de instalación del monitor en la barra

𝑖, 𝑁 es el número total de barras y 𝑁_𝑝𝑓 es el número total de locaciones de falla establecido en el análisis de cortocircuito realizado.

En (4) se presenta una formulación alternativa de (3), donde la información topológica de la red permite una simplificación de la AAM [16]–[18]. La nueva matriz simplificada adopta el concepto de Área Topológica de Alcance del Monitor (ATAM). La simplificación consiste en una sustitución de los valores diferentes de cero en la matriz. Esto es derivado teniendo en cuenta que, en un sistema eléctrico radial, las barras aguas abajo de un punto en falla tendrán tensiones residuales muy cercanas a cero.

𝑁

min 𝑓(𝑥) = ∑ 𝑐_𝑖 · 𝑥_𝑖

𝑖=1

    (4)

𝑁

sujeto a:  ∑ 𝐀𝐓𝐀𝐌_(𝑖,𝑘) ∗ 𝑥_𝑖 ≥ 1,    𝑘 = 1, 2 , … , 𝑁_𝑝𝑓

𝑖

Los trabajos referenciados en esta sección mantienen la misma estructura del problema de optimización mostrada en (3) y (4). Se caracterizan por formular una única restricción de observabilidad de los hundimientos de tensión, sin tener en cuenta criterios adicionales con relación a la localización de la fuente generadora de las fallas; siendo algunas de las nuevas propuestas innovadoras en esta área de investigación que pretenden maximizar los beneficios de los nuevos sistemas de monitorización inteligente.

3. UBICACIÓN   ÓPTIMA DE   MONITORES INCORPORANDO RESTRICCIONES DE LOCALIZACIÓN RELATIVA DE FALLAS DE RED

A continuación, se discuten dos nuevos aspectos en relación con el problema de ubicación óptima de monitores de hundimientos de tensión. 

a) Los métodos de ubicación óptima no están siendo formulados en función de los requerimientos para implementar nuevas técnicas de gestión avanzada en los sistemas de distribución. Por lo tanto, nuevas capacidades de análisis y toma de decisiones no se fortalecen, cuando lo correcto son nuevas y mejores herramientas como respuesta a las significativas inversiones realizadas en los sistemas de monitorización. En este artículo se consideran dos técnicas de gestión avanzada como objeto de interés: la localización relativa de fallas y la estimación de estado de los hundimientos de tensión, ambas usando la información registrada por un óptimo sistema de monitorización.

b) Los métodos de ubicación óptima de monitores requieren ser implementados en redes de distribución con características reales, caracterizadas por desbalances, alimentados y ramales trifásicos, bifásicos y monofásicos; además en la validación de resultados, se requiere el análisis del impacto de la naturaleza estocástica de las fallas en la red y sus impedancias de falla. 

c) A partir de lo previamente expuesto, a continuación, se propone un nuevo método que incorpora, dentro de la formulación del problema de optimización, restricciones de observabilidad derivadas de una técnica de localización relativa de fallas en la red.

3.1. Método propuesto para la ubicación óptima de monitores de hundimientos de tensión

La metodología propuesta se basa en la determinación de las MOHT, una por cada tipo de falla (Línea-tierra (LT); línea-línea (LL); línea-línea-tierra (LLT); 3-líneas (LLL) y 3-líneas-tierra LLLT), usando el método de LF para su construcción. Los aspectos relevantes del método propuesto se describen a continuación.

a) El enfoque abordado en [11] establece una metodología para la ubicación relativa de la fuente de un hundimiento de tensión. Se basa principalmente en la existencia de nodos en los alimentadores donde se presentan derivaciones en alimentadores secundarios. Esto se puede observar en la Figura 1, donde se muestra el diagrama unifilar de la red de distribución de prueba de 34 barras-IEEE. Se identifica un ramal principal y 8 ramales en derivación. Estos puntos de derivación son de interés y son priorizados para ubicar monitores de hundimientos de tensión en estas locaciones.  Por lo tanto, la restricción de la localización relativa de fallas en la red se formula a partir de esta información. Según se presenta en [11], un método de localización relativa de la fuente de los hundimientos de tensión permite identificar zonas de localización de fallas que resulta en información útil, entre otras cosas para la operación de los sistemas de distribución y la estimación de estado de hundimientos de tensión.

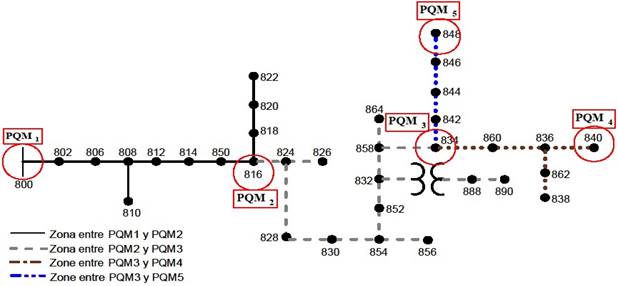
Figura 1. Red de distribución de 34 nodos. Zonas de localización relativa de fallas de red.  Fuente: [11].

b) El número y la selección de los puntos en derivación como candidatos a la instalación de monitores está condicionado a: la topología de red, la longitud de los alimentadores y las zonas de red establecidas por los puntos en derivación seleccionados (Figura 1). Además, también se tiene en cuenta el tipo de usuario en la zona de red y la frecuencia de falla del tramo de red. Estos criterios dependerán también de las condiciones de operación del sistema eléctrico y de la necesidad particular de monitorización.

c) Se busca evaluar la sensibilidad en la solución del problema de optimización cuando se consideran diferentes valores de impedancia de falla en la construcción de la MOHT: un valor mínimo 𝑍_{𝑓𝑚𝑖𝑛} de 0 Ω, que es el valor más común usado en muchos de los trabajos revisados; un valor medio 𝑍_{𝑓𝑚𝑒𝑑} y un valor máximo 𝑍_{𝑓𝑚𝑎𝑥}, caracterizados a partir de un estudio estadístico de eventos de falla reales registrados en la red de distribución objeto de estudio.  Se busca caracterizar la sensibilidad del número de monitores a instalar de acuerdo a la solución del problema de optimización en cada caso.

3.2. Definición de la Matriz de Derivaciones (MD)

Los nodos en derivación se definen en (5), usando una matriz diagonal binaria MD. Aunque aparentemente es trivial esta condición de conocer estos puntos previamente y se piense en eliminar estas variables del problema de optimización, esto no puede llevarse a cabo debido a la condición de observabilidad que es evaluada en cada posible configuración de monitores en la red de distribución. Los elementos de la matriz MD son ceros, excepto aquellos de la diagonal que correspondan a los nodos de derivación presentes en los alimentadores y los cuales son seleccionados aplicando criterios operativos del sistema eléctrico.

(𝑖,𝑖) = {0 ,1𝑠𝑖, 𝑠𝑖 𝐌𝐃 𝐌𝐃𝑖𝑖 𝑖𝑖no es un nodo de derivación                                                           (5)

Adicionalmente, se define el vector columna binario b, cuyos valores son cero, excepto aquellos en donde 𝑏_𝑖 corresponde a un punto de derivación.

3.3. Formulación del problema de optimización

Una vez definida la MD, se procede a formular el nuevo problema de optimización para garantizar la observabilidad en toda la red, incluyendo restricciones de localización de fallas. El objetivo es minimizar el costo del conjunto de monitores de hundimientos de tensión a instalar, tal como se muestra en (6).

𝑁

min 𝑓(𝑥) = ∑ 𝑐_𝑖 · 𝑥_𝑖

𝑖=1

  sujeto a: 

𝑁

∑ _(𝑖,𝑘) ∗ 𝑥_𝑖 ≥ 1,    𝑘 = 1, 2 , … , 𝑁_𝑝𝑓

𝑖

(6)

𝐌𝐃 · 𝐱 = 𝐛

En (6), 𝑐_𝑖 es el costo de instalación del monitor en la barra 𝑖, 𝑁 es el número total de barras y 𝑁_𝑝𝑓 es el número total de puntos de falla.

En la Figura 2 se presenta el diagrama de flujo del método propuesto para determinar el arreglo óptimo de monitores de hundimientos de tensión, teniendo en cuenta restricciones de localización de fallas en la red. 

 De forma concreta, los pasos para la aplicación de la metodología son los siguientes:

1) Los datos de entrada son los parámetros y la topología de red del sistema de distribución objeto de estudio.

2) Se realiza un análisis de cortocircuito mediante simulación en todas las barras y locaciones de línea que se definan el sistema eléctrico. Para ello se recomienda establecer puntos de falla a intervalos de 100 metros en promedio, siendo una segmentación apropiada en este tipo de redes eléctricas [19]. El valor de la impedancia de falla 𝑍_𝑓 es el mismo para todas las fallas realizadas, y de acuerdo a lo expresado previamente, se establecen tres valores distintos (𝑍_{𝑓𝑚𝑖𝑛}, 𝑍_{𝑓𝑚𝑒𝑑}, 𝑍_{𝑓𝑚𝑎𝑥}). Para cada impedancia de falla, se obtiene un conjunto de fallas que son etiquetadas y agrupadas separadamente.

3) Se determina la matriz AAM para un umbral de 0.9 p.u y para todos los tipos de falla (LT, LL, LLT, LLL y LLLT). Seguidamente se establece la matriz MD y el vector b, de acuerdo a los criterios de selección de los nodos de derivación descritos en la sección 3.1.

4) Se resuelve el problema de optimización presentado en (6). Se obtiene una solución óptima por cada tipo de falla y por cada 𝑍_𝑓 usada en el análisis de cortocircuito. En este trabajo se emplea programación entera mixta como método de solución del problema de optimización planteado.

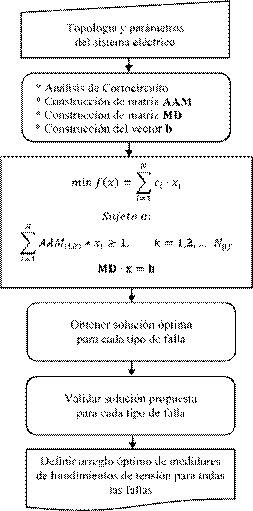
Figura 2. Método propuesto para la ubicación óptima de monitores de hundimientos de tensión. Fuente: Elaboración propia.

Se realiza una validación de la observabilidad de los hundimientos de tensión de acuerdo a la solución obtenida; esto es realizado para cada tipo de falla mediante la simulación de nuevos escenarios de falla no contemplados en el paso 2. Para ello se establecen simulaciones de Monte Carlo usando las estadísticas de falla reales provistas por el operador de red.

5) Finalmente, se define el arreglo óptimo de monitores de hundimientos de tensión que cumpla las restricciones de observabilidad para todos los tipos de falla, permitiendo un esquema de localización relativa de las fallas en la red.

4. CASO DE ESTUDIO: RED DE DISTRIBUCIÓN REAL DE 13,2 KV

Con el fin de validar la efectividad de la metodología propuesta, se presentan los resultados obtenidos tras aplicar la metodología en un sistema de distribución real de un operador de red en Colombia. El estudio de cortocircuito se realizó usando el software ATP – EMP y la solución del problema de optimización se llevó a cabo usando las herramientas de programación entera mixta de

MATLAB. 

4.1. Características de la red de distribución de prueba

En la Figura 3 se presenta la red real de distribución de energía eléctrica de un operador de red en Colombia caracterizado por contar con segmentos de red trifásicos, bifásicos y monofásicos. Además, tiene 379 barras (de los cuales 153 poseen carga y 4 cuentan con equipos de compensación capacitiva). La tensión nominal de operación es de 13,2 kV y la carga típica de operación es de 5,3 MW, con una compensación capacitiva total que alcanza los 1,05 MVAr.

4.2. Construcción de las matrices AAM y MD

A partir de los datos históricos de impedancia de falla para la red eléctrica en estudio, se realizaron 3 análisis de cortocircuito con 𝑍_𝑓 igual 0 Ω, 10 Ω y 20 Ω, fallando todos los nodos de la red y teniendo en cuenta las tensiones del estado pre-falla, así como los efectos de la carga durante el estado de falla. 

Los puntos de derivación de la red eléctrica se establecieron en los nodos 5, 111, 239 y 353. Esto se deduce a partir de los criterios descritos en la sección 3.1. Consecutivamente se construyen las matrices de observabilidad y de derivación para cada tipo de falla con un umbral de tensión de 0,9 p.u. 

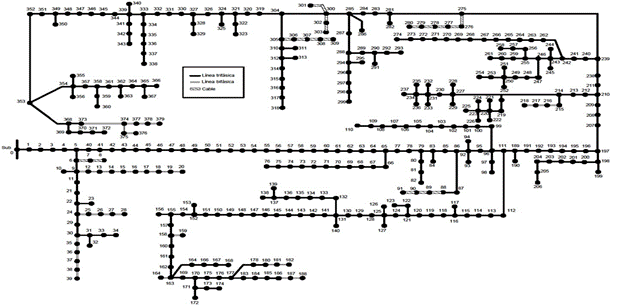
Figura 3. Red de distribución real de 379 barras. Fuente: Elaboración propia.

4.3. Resultados y discusión

En la Tabla 1 se presentan los arreglos óptimos de monitores, obtenidos por un lado con el concepto clásico del AAM y por otro lado, con el método propuesto en este artículo. 

Tabla 1. Esquemas óptimos de monitorización: método clásico y propuesto.

	Número de monitores / barras
𝒁𝒇	Método Clásico AAM	Método Propuesto
0 Ω	2 / {95;218}	5 / {5;111;218;239;353}
10 Ω	-	5 / {5;111;239;353;356}
20 Ω	-	5 / {5;111;164;239;353}

Fuente: Elaboración propia.

Tabla 2. Estadísticas de falla del sistema en estudio.

MC	Tasa de fallas	𝒁𝒇	Tipo de Falla	Total
1	40 fallas/año Fdp Poisson	µ= 10Ω σ= 5 Ω Fdp Normal	LT= 72% Fase A= 23,6  Fase B = 31,7  Fase C=17,1  LL= 11% Fases AB=4,1 Fases BC =3,3 Fases CA =3,3 LLT= 6% Fases AB =3,3 Fases BC =2,4 Fases CA =0 LLL= 11% Fases ABC =8,9 Fases ABCT =2,4 Punto de falla aleatorio Fdp Uniforme	20 años: 766 fallas
2		µ= 1 Ω σ=0.5Ω Fdp Normal		1 año: 43 fallas
3		µ= 30Ω σ= 15Ω Fdp Normal		1 año: 42 fallas

Fuente: Elaboración propia.

Una vez establecido el arreglo de monitores según la Tabla 1, se evaluó el desempeño en la detección de hundimientos de tensión. Para esto se realizó una evaluación estocástica mediante tres simulaciones de Monte Carlo con las estadísticas presentadas en la Tabla 2. Finalmente se aplicó el factor de observabilidad de

hundimientos de tensión FO, mostrado en (7),

ℎ𝑡𝑜𝑏

𝑭𝑶 (%) =  x 100                     (7)

𝑇ℎ𝑡𝑜𝑏

donde ℎ𝑡𝑜𝑏 es el número de hundimientos de tensión observados por lo menos por un monitor y  𝑇ℎ𝑡𝑜𝑏 es el número total de fallas en la red que generan hundimientos de tensión, los cuales son experimentados por al menos un usuario.

En la Figura 4 se presenta el comportamiento del 𝑭𝑶 para el método clásico que usa el concepto de AAM y para el método propuesto. Se analizan los tres escenarios de Monte Carlo construidos a partir de los datos descritos en la Tabla 2. 

Los resultados presentados en la Figura 4 validan el bajo rendimiento del método clásico basado en la AAM, a la hora de garantizar la observabilidad, a medida que la resistencia de falla aumenta. Respecto a la metodología propuesta, se consigue una observabilidad dentro de rangos aceptables para los escenarios analizados (0 Ω, 10 Ω y 20 Ω). Además, también se puede observar que la instalación de cinco (5) monitores (barras 5, 111, 239, 353 y 356) cumplen las restricciones de observabilidad y de localización relativa de fallas en la red. Esto se logra mientras se mantiene un aceptable factor de observabilidad de hundimientos de tensión para cada una de las fallas registradas en la red de distribución objeto de estudio. 

En redes de distribución de energía eléctrica altamente sensibles a hundimientos de tensión, como es el caso estudiado en este trabajo, se concluye que es menor el número de monitores necesarios para garantizar únicamente la observabilidad, en comparación con los monitores requeridos para cumplir las restricciones de localización relativa de fallas. Sin embargo, siempre debe ser evaluada de forma simultánea las dos restricciones para llegar a un arreglo óptimo de monitores que garanticen el desempeño esperado bajo condiciones reales en los sistemas de distribución.

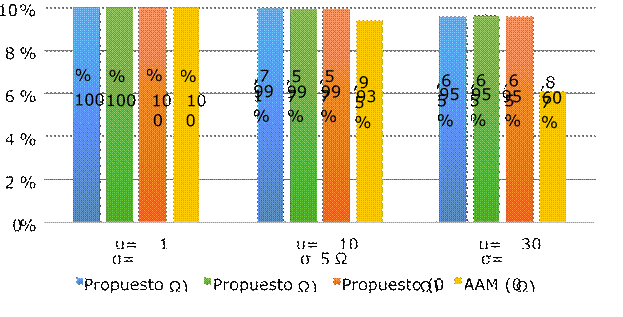
Figura 4. Comportamiento de 𝑭𝑶 para los métodos clásico y propuesto en los escenarios Montecarlo. Fuente: Elaboración propia.

5. CONCLUSIONES

Los retos en la operación eficiente de los sistemas de distribución conllevan a una contaste búsqueda de nuevas propuestas metodológicas que exploten las capacidades provistas por los nuevos desarrollos tecnológicos en el sector eléctrico. Es así como los sistemas de monitorización requieren ser diseñados desde sus capacidades y proyecciones en la gestión avanzada de las redes de distribución. La propuesta metodológica en este trabajo se enfoca en la ubicación óptima de monitores de hundimientos de tensión, incorporando un nuevo conjunto de restricciones de observabilidad. Los resultados del factor de observabilidad evidencian el eficiente desempeño del método propuesto en las simulaciones de Monte Carlo, donde un conjunto amplio de fallas de red es generado para evaluar la robustez del sistema de monitorización en la detección de hundimientos de tensión. La implementación del método propuesto permitiría el control y mejoramiento de los indicadores de la calidad de la potencia eléctrica, reducción del tiempo de restauración del servicio de energía eléctrica y, en general, la disminución de pérdidas económicas tanto para los operadores de red como para los usuarios de servicio de energía eléctrica.

6. REFERENCIAS

[1] V. Vega Garcia, C. Duarte Gualdrón, and G. Ordonez Plata, “Aplicación de la Transformada Wavelet Discreta (dwt) en la Detección e Identificación de Eventos de la Calidad de la Energía Eléctrica,” Rev. UIS Ing., vol. 5, no. 1, pp. 109–118, Dic, 2006.

[2] J. H. Duarte, A. Peñuela A., G. Ordonez Plata, J. Pacheco López, and J. Duarte Duarte, “Propuesta Metodológica Para La Valoracion De Costos Debidos a Una Inadecuada Calidad De La Continuidad Del Suministro De La Energía Eléctrica,” Rev. UIS Ing., vol. 4, no. 1, pp. 18–24, Jul –Dic, 2017.

[3] A. A. Ibrahim, A. Mohamed, H. Shareef, and S. P. Ghoshal, “Optimal placement of voltage sag monitors based on monitor reach area and sag severity index,” Proceeding, 2010 IEEE Student Conf. Res. Dev. - Eng. Innov. Beyond , no. SCOReD, pp. 467–470, Dic, 2010.

[4] S. Jamali, A. Bahmanyar, and E. Bompard, “Fault location method for distribution networks using smart meters,” Measurement, vol. 102, pp. 150–157, 2017.

[5] T. R. Kempner, M. Oleskovicz, and A. Q. Santos, “Optimal allocation of monitors by analyzing the vulnerability area against voltage sags,” Proc. Int. Conf. Harmon. Qual. Power, ICHQP, pp. 536–540, 2014.

[6] A. Kazemi, A. Mohamed, H. Shareef, and H. Zayandehroodi, “Optimal power quality monitor placement using genetic algorithm and Mallow’s Cp,” Int. J. Electr. Power Energy Syst., vol. 53, pp. 564–575, 2013.

[7] C.-F. Almeida and N. Kagan, “Harmonic State Estimation Through Optimal Monitoring Systems,” IEEE Trans. Smart Grid, vol. 4, no. 1, 2013.

[8] J. Blanco Solano, J. F. Petit, and G. Ordonez Plata, “Optimal placement of voltage sag monitors in smart distribution systems: Impact of the dynamic network reconfiguration,” IEEE PES Innovative Smart Grid Technologies Latin America, 2015, pp. 361–365. [9] S. Nasiri and H. Seifi, “Robust probabilistic optimal voltage sag monitoring in presence of uncertainties,” IET Gener. Transm. Distrib., vol. 10, no. 16, 2016.

[9] G. Morales España, H. Vargas Torres, and J. Mora Flórez, “Influencia de la Variación en la Carga y del Tamaño de la Zona en la Precisión de un Localizador de Fallas para Circuitos de Distribución,” Rev. UIS Ing., vol. 6, no. 1, pp. 47–57, 2007.

[10] J. Blanco Solano, J. F. Petit Suárez, and G. O. P. Ordóñez Plata, “Methodology for Relative Location of Voltage Sags Source using Voltage Measurements Only,” Dyna, vol. 82, no. 192, pp. 94–100, 2015.

[11] G. Olguin, F. Vuinovich, and M. H. J. Bollen, “An optimal monitoring program for obtaining voltage sag system indexes,” IEEE Trans. Power Syst., vol. 21, no. 1, pp. 378–384, 2006.

[13] M. Haghbin, E. Farjah, and H. Mazaherifar, “Improved power quality monitor placement using innovative indices,” 4th Annu. Int. Power Electron. Drive Syst. Technol. Conf., no. 1, pp. 501–509, 2013.

[14] T. R. Kempner, F. A. Mourinho, F. B. Bottura, M. Oleskovicz, J. C. M. Vieira, and J. R. L. Filho, “Optimal voltage sags monitoring considering different loading profiles in distribution systems,” Int. Conf. Renew. Energies Power Qual., no. 14, 2016.

[15] T. R. Kempner, M. Oleskovicz, and D. P. S. Gomes, “Optimal monitoring of voltage sags through simultaneous analysis of short-circuits in distribution systems,” IET Gener. Transm. Distrib., vol. 11, no. 7, pp. 1801–1808, 2017.

[16] L. A. Wong, H. Shareef, A. Mohamed, and A. A. Ibrahim, “Novel quantum-inspired firefly algorithm for optimal power quality monitor placement,” Front. Energy, vol. 8, no. 2, pp. 254–260, 2014.

[17] A. A. Ibrahim, A. Mohamed, and H. Shareef, “Optimal power quality monitor placement in power systems using an adaptive quantum-inspired binary gravitational search algorithm,” Int. J. Electr. Power Energy Syst., vol. 57, pp. 404–413, 2014.

[18] D. P. S. Gomes, M. Oleskovicz, T. R. Kempner, J. R. L. Filho, P. Quality, M. Allocation, and G. Coverage, “A generalized coverage matrix method for power quality monitor allocation utilizing genetic algorithm,” Int. Conf. Renew. Energies Power Qual., no. 14, 2016.

[19] M. Majidi, A. Arabali, and L. S. Member, “Fault Location in Distribution Networks by Compressive Sensing,” IEEE Trans. Power Deliv., vol. 8977, no. c, pp.

1–8, 2014.