INTRODUCTION
Compressive sensing (CS) establishes that a given signal can
be recovered from far fewer samples than those required by the Shannon-Nyquist
criterion. As a consequence, through the years some sensors to acquire multidimensional
signals as spectral images or video from less samples have been developed.
Particularly, spectral multiplexing sensors based on CS attempt to break the
Nyquist barrier by acquiring 2D projections of a scene in order to obtain a
high spectral resolution image. The most remarkable CS sensor for spectral
imaging is called the coded aperture snapshot spectral imager (CASSI) which is
composed by a few set of elements such as a lenses set, a coded aperture, a
dispersive element and a focal plane array (FPA). Particularly, the colored
CASSI or C-CASSI is a version of CASSI where the coded aperture is a colored
coded aperture (CCA) which leads a richer encoding procedure [1, 2, 3].
Figure 1 illustrates the set of elements in the C-CASSI. The
principal characteristic of a CCA relies on the fact that each CCA pixel can
spectrally encode the incoming light letting to pass just a desired set of
wavelengths. Hence, the CCA pixels can operate on the spectral axis as
frequency-selective filters, i.e. as low pass (L), band pass (B) or high pass (H)
optical filters. In other words, each pixel lets to pass certain frequency
components of the source pixel and totally rejects all others. Thus, each CCA
pixel is one of many possible optical filters whose spectral response can be
selected. Figure 1(b) shows an illustration of the above-mentioned filters
where each CCA pixel color corresponds to a specific spectral response: Low,
High and Band pass filter, respectively. Further, the filters in the CCA can be
selected at a randomly form or they can be optimally selected such that the
number of projections is minimized while the quality of reconstruction is
maximized [1].
The C-CASSI permits the compressive acquisition of a 3D
spectral image into a 2D detector. Further, the C-CASSI extended to video
(video C-CASSI) is a spectral multiplexing sensor that allows capturing
spectral dynamic scenes, or spectral video, by projecting each spectral frame
onto a bidimensional detector [4, 5, 6]. A spectral video is considered as a four-dimensional
signal 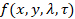 , where
, where 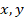 denote the spatial
pixels,
denote the spatial
pixels, 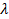 represents the spectral dimension
and
represents the spectral dimension
and 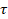 denotes
the temporal component.
denotes
the temporal component.
The spectral video has many applications in the industry and
the academy, such as surveillance, moving targets recognition, security, and
classification, where the discrimination of the features is performed over the
different spectral bands instead of use only three channels (RGB) as in
traditional approaches [7, 8, 9, 10]. Figure 2 shows the sensing process in the
video C-CASSI system for a spectral video. Basically, in the sensing process,
the incoming light is encoded by the coded aperture 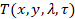 , and then, the coded
light is spectrally dispersed by the dispersive element, usually a prism.
, and then, the coded
light is spectrally dispersed by the dispersive element, usually a prism.
Finally, the encoded and dispersed light is integrated in
the FPA.The compressed video is reconstructed iteratively by finding a sparse
solution to an undetermined linear system of equations.
However, recovering a compressed video entails diverse
challenges originated by the temporal variable. The scene motion during the
acquisition yields to motion artifacts, and these artifacts get aliased during
the video reconstruction damaging the entire data [11]. As a result,
multiresolution approaches have been proposed in order to alleviate the
aliasing and enhance the video reconstruction. The idea of interpret the data
at multiple resolutions have been called the “chicken-and-egg” problem, which
states that reconstructing a high-quality CS video could be obtained adding
temporal correlation such as motion compensation, and computing motion
compensation requires knowledge of the full video.
Works such as [12, 13] propose a preview reconstruction to
estimate the motion field in the video such that it can be used to achieve a
high-quality reconstruction. However, these approaches have been focused in
spatial or temporal multiplexing architectures while the spectral information
in the video has been discarded.
This work presents a modification to the compressive
spectral video recovery step adding an additional regularization term to
correct the errors induced by the motion. Thus, the motion estimated from a low
spatial resolution version, or a preview, is imposed as prior information in
the optimization problem. This approach aims to correct the artifacts induced
by the motion in the reconstruction problem following a multiresolution
strategy. Hence, this scheme allows going from a low to a high spatial
resolution in the reconstruction, in order to obtain an improvement in the
spatial quality of the reconstructed spectral video. In the following sections,
it is introduced the discrete model of the CASSI system using colored coded
apertures extended to spectral video acquisition. Next, the multiresolution
strategy for compressive spectral video reconstruction is developed, and then,
a quantitative comparison to measure the performance of the proposed approach
is presented.
COMPRESSIVE SPECTRAL VIDEO C-CASSI MODELING
Discrete sampling model for video C-CASSI
Let 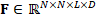 be
the discretized-form of a given spectral video, with N × N spatial
pixels, L spectral bands and D spectral frames; then, the sensing
process of F through the video C-CASSI system can be modeled as the
linear projection of the vectorized form of the source
be
the discretized-form of a given spectral video, with N × N spatial
pixels, L spectral bands and D spectral frames; then, the sensing
process of F through the video C-CASSI system can be modeled as the
linear projection of the vectorized form of the source 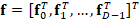 ,
where
,
where 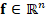 with
with
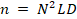 , onto
the matrix H as
, onto
the matrix H as
|
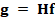 , ,
|
(1)
|
where g ∈
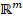 represents
the vectorized form of the compressive measurements on the detector, with
represents
the vectorized form of the compressive measurements on the detector, with 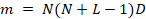 . For the recovery of
the compressive spectral video, CS exploits the fact that many signals can be
represented in a sparse form in some representation basis. Formally, the given
spectral video signal
. For the recovery of
the compressive spectral video, CS exploits the fact that many signals can be
represented in a sparse form in some representation basis. Formally, the given
spectral video signal 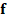 can be
expressed as
can be
expressed as 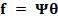 ,
where
,
where 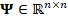 is
a representation basis such as a Wavelet or Cosine, and
is
a representation basis such as a Wavelet or Cosine, and 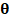 denotes
the nonzero coefficients of the signal in the given basis
denotes
the nonzero coefficients of the signal in the given basis 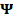 .
.
Hence, the Eq. (1) can be rewritten as
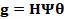 . (2)
. (2)
Inverse problem
Solving the problem in Eq. (1) requires the inversion of the
linear system, however, since the number of the measurements 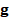 is
significantly smaller than the number of columns in
is
significantly smaller than the number of columns in 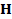 , i.e.
, i.e.
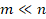 , the
direct inversion of the system is not feasible. Then, the compressed signal
reconstruction is performed iteratively by finding a sparse solution to Eq. (2)
given by the optimization problem expressed as
, the
direct inversion of the system is not feasible. Then, the compressed signal
reconstruction is performed iteratively by finding a sparse solution to Eq. (2)
given by the optimization problem expressed as
|
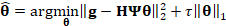 , ,
|
(3)
|
where ‖⋅‖_2^2
is the square l_2 -norm that measures the mean square error of the estimation, ‖⋅‖_1 is the l_1-norm that measures
the nonzero values in the vector and τ is a regulator which penalizes searching
the sparsest solution. However, notice that the optimization problem presented
in Eq. (3) does not consider the motion in the compressive measurements. In
other words, this optimization problem searches a sparse solution for static
images, hence, some motion artifacts are produced in the spectral video reconstruction
process damaging the entire data and producing low spatial quality
reconstruction.
MULTIRESOLUTION RECONSTRUCTION APPROACH FOR COMPRESSIVE SPECTRAL VIDEO
SENSING
Briefly, the proposed multiresolution reconstruction
approach is based on the reconstruction of a low spatial resolution version of
the spectral video in order to extract the temporal or motion information.
Then, the motion information is added as an additional regularization term in
the optimization problem to correct motion artifacts and enhance the
reconstruction quality of the high resolution spectral video.
More formally, for the low-resolution estimation, a spatial
down-sampling operator 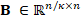 ,
, 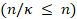 , is
introduced in Eq. (1) such that the measurements are rewritten as
, is
introduced in Eq. (1) such that the measurements are rewritten as
|
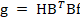 , ,
|
(4)
|
where BT is the transpose of B.
Then, an  −
− 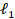 -norm
algorithm to solve the minimization problem presented in Eq. (3) is used with
few iterations to obtain the sparsest coefficients of a coarse reconstruction
of the spectral video from the measurements as
-norm
algorithm to solve the minimization problem presented in Eq. (3) is used with
few iterations to obtain the sparsest coefficients of a coarse reconstruction
of the spectral video from the measurements as
|
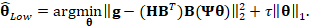
|
(5)
|
Then, the low-resolution version of the spectral video is
estimated by
|
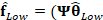 ), ),
|
(6)
|
where 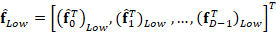 represents
the low spatial resolution version.
represents
the low spatial resolution version.
The obtained coarse estimation 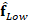 is
up-sampled and then, used to extract the motion of the video as the optical
flow.
is
up-sampled and then, used to extract the motion of the video as the optical
flow.
The optical flow estimation between any two frames 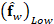 and
and
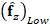 , for
, for 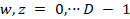 and
and 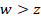 , is given by
, is given by 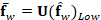 ,
where U is an up-sampling operator such as a “bilinear interpolation”.
Then, the optical flow is estimated from any two frames
,
where U is an up-sampling operator such as a “bilinear interpolation”.
Then, the optical flow is estimated from any two frames 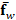 and
and 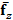 by
computing the changes in the horizontal
by
computing the changes in the horizontal 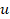 and
vertical
and
vertical 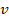 axis as in [14]. Then, for an
estimation of the spectral video, the motion errors can be expressed as
axis as in [14]. Then, for an
estimation of the spectral video, the motion errors can be expressed as
|
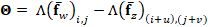 , ,
|
(7)
|
where 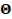 represents
the error induced by the scene motion,
represents
the error induced by the scene motion, 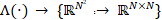 is
an operator that arranges a vector in matrix form, and
is
an operator that arranges a vector in matrix form, and 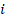 ,
, 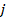 goes over the
spatial dimension of the selected frame.
goes over the
spatial dimension of the selected frame.
Following the Eq. (7) to compute the motion errors, the
optimization problem in Eq. (3) can be rewritten as
|
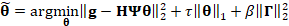 , ,
|
(8)
|
where β is a regularizer parameter and 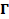 is
defined as
is
defined as
|
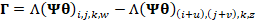 , ,
|
(9)
|
where  with
with 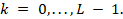 Notice
that in Eq. (9) the subindex
Notice
that in Eq. (9) the subindex 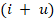 and
and 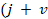 ) accounts for the
horizontal and vertical changes, respectively.
) accounts for the
horizontal and vertical changes, respectively.
For illustration purposes, Figure 3 shows the optical flow
estimation following a color map representation with the horizontal and
vertical changes. Notice that in Fig. 3, the Frame 1 changes with respect to
Frame 2 in the horizontal axis. Then, the optical flow representation adopts
the respective colors given by the color map for the left and right movements
[14].
To solve the problem in Eq. (8), it can be used well-known
implementations of signal recovery such as the LASSO or the GPSR algorithm by
adding the regularization term as shown in Eq. (8) [15]. Finally, the
reconstruction of the signal is attained by
|
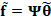 , ,
|
(10)
|
where 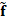 is the reconstructed spectral video in
vector form.
is the reconstructed spectral video in
vector form.
RESULTS
To evaluate the performance of the proposed multiresolution
reconstruction, a set of compressive measurements is simulated using the
forward model in Eq. (1). For this, four test spectral videos were selected as
follows. The first and the second dataset are cropped sections of the spectral
video taken from [16] called Boxes 1 and Boxes 2, respectively.
The third dataset, called Beads, is a synthetic spectral video of a
moving object over a spectral static scene [17], and the fourth dataset, called
Chiva bus, is a real sequence of spectral images acquired in the Optics
Lab of the High Dimensional Signal Processing (HDSP) research group of the
Universidad Industrial de Santander. All the datasets were acquired with a CCD
camera and a VariSpec Liquid Crystal Tunable Filter (LCTF) in wavelengths from
400 nm to 700 nm at 10 nm steps. A spatial section of N × N pixels
with N = 128, L = 8 spectral bands and D = 8 frames was
used for simulations. Specifically, the L selected wavelengths were 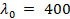 ,
, 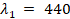 ,
, 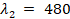 ,
, 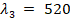 ,
, 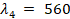 ,
, 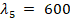 ,
, 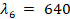 and
and 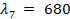 nm.
Figure 4 presents an RGB profile of the four test spectral videos.
nm.
Figure 4 presents an RGB profile of the four test spectral videos.

Figure 4. RGB representation of the eight frames for the
four spectral videos used in the simulations. The resolution of each video is 128
× 128 spatial pixels, 8 spectral bands and 8 spectral frames.
For the numerical simulation of the video C-CASSI system
illustrated in Fig. 1, it was used a random and an optimized colored coded
aperture (CCA) with low and high band pass filters denoted by 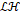 -random
CCA and
-random
CCA and 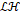 -CCA,
respectively [1]. Further, in order to test the proposed multiresolution-based
reconstruction, the different measurements attained with the aforementioned
coded apertures realizations were reconstructed by using the GPSR algorithm
adding the above-mentioned regularization term [15]. The peak signal-to-noise
ratio (PSNR) metric is used to assess the image quality of the reconstructions.
The PSNR is related with the mean square error (MSE) error as
-CCA,
respectively [1]. Further, in order to test the proposed multiresolution-based
reconstruction, the different measurements attained with the aforementioned
coded apertures realizations were reconstructed by using the GPSR algorithm
adding the above-mentioned regularization term [15]. The peak signal-to-noise
ratio (PSNR) metric is used to assess the image quality of the reconstructions.
The PSNR is related with the mean square error (MSE) error as 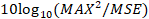 where
where
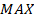 is
the maximum possible value of the image and the measure is given in decibels
(dB). All simulations were performed using the MATLAB software R2015a under the
license Total Academic Headcount of the Universidad Industrial de
Santander in an Intel Core i7 3.6 GHz processor and 16 GB RAM memory.
is
the maximum possible value of the image and the measure is given in decibels
(dB). All simulations were performed using the MATLAB software R2015a under the
license Total Academic Headcount of the Universidad Industrial de
Santander in an Intel Core i7 3.6 GHz processor and 16 GB RAM memory.
Multiresolution reconstructions
The low-resolution version for the multiresolution
reconstruction was estimated with a spatial resolution of 32 × 32 pixels, i.e.
a spatial down-sampling by a factor of 4. The high-resolution reconstruction is
performed following both the traditional and the proposed reconstruction by
using the sparse solution attained from Eq. (3) and Eq. (8), respectively.
Figure 5 shows an RGB representation of the frame 2 from the reconstructed
videos (a) Boxes 1, (b) Boxes 2, (c) Beads and (d) Chiva
bus with the proposed multiresolution reconstruction. For each coded
aperture used, the averaged PSNR is shown.

Figure 5. RGB representation of the frame 2 from the
reconstructed videos: (a) Boxes 1, (b) Boxes 2, (c) Beads
and (d) Chiva bus, using the proposed reconstruction approach. First row
presents the reconstruction using 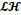 -CCA,
and second row using the
-CCA,
and second row using the 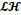 -random
CCA. The averaged PSNR across the spectral bands is shown for each case.
-random
CCA. The averaged PSNR across the spectral bands is shown for each case.
Figure 6 illustrates three original spectral bands for the
2nd frame of the Chiva bus video, and its respective reconstructions
using the multiresolution approach. Each wavelength and the quality of reconstruction
in terms of PSNR are shown.

Figure 6. Original (first column) and reconstructions of 3
spectral bands for the frame 2 of the Chiva bus video by using 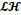 -CCA
(second column) and the
-CCA
(second column) and the 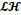 -random
CCA (third column) coded apertures. The quality reconstruction in terms of PSNR
is shown for each spectral band.
-random
CCA (third column) coded apertures. The quality reconstruction in terms of PSNR
is shown for each spectral band.
Multiresolution reconstruction vs. Traditional reconstruction
Table 1 presents the summarization of the results in terms
of averaged PSNR for the 2 coded aperture patterns used and both reconstruction
methods. In general, observe that the obtained PSNR values with the
multiresolution-based reconstruction are higher than those obtained with the
traditional reconstruction.
Table 1. PSNR mean across the four dimensions for the
traditional and multiresolution reconstruction.
|
PSNR(dB) mean
|
|
Traditional reconstruction
|
Boxes 1
|
Boxes 2
|
Beads
|
Chiva bus
|
|
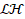 -CCA -CCA
|
32,17
|
31,6
|
26,68
|
30,07
|
|
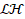 -Random
CCA -Random
CCA
|
31,46
|
31,6
|
26,41
|
30,2
|
|
Multiresolution reconstruction
|
|
|
|
|
|
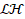 -CCA -CCA
|
34,52
|
33,45
|
30,53
|
31,17
|
|
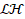 -Random
CCA -Random
CCA
|
34,7
|
33,58
|
30,09
|
31,06
|
Notice that the multiresolution-based reconstruction
proposed outperforms the traditional reconstruction in up to 4 dB.
CONCLUSION
The multiresolution reconstruction for compressive spectral
video sensing in the video C-CASSI architecture has been proposed in this
paper. For this, a low-resolution version is reconstructed using a few
iterations of a  −
− 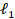 -norm
recovery algorithm. Later, from the low-resolution reconstruction, the optical
flow is estimated to obtain the scene motion. The multiresolution-based
reconstruction attempts to reduce the error originated by the temporal variable
adding the scene motion as an additional regularization term in the
minimization problem. Simulations show a reconstruction quality improvement
using the proposed reconstruction up to 4 dB of PSNR with respect to the
traditionally reconstruction.
-norm
recovery algorithm. Later, from the low-resolution reconstruction, the optical
flow is estimated to obtain the scene motion. The multiresolution-based
reconstruction attempts to reduce the error originated by the temporal variable
adding the scene motion as an additional regularization term in the
minimization problem. Simulations show a reconstruction quality improvement
using the proposed reconstruction up to 4 dB of PSNR with respect to the
traditionally reconstruction.
ACKNOWLEDGMENT
The authors gratefully acknowledge the Vicerrectoría de
Investigación y Extensión of Universidad Industrial de Santander for supporting
this research registered under the project titled: “Diseño y simulación de un
sistema adaptativo de sensado compresivo de secuencias de video espectral” (VIE
code 1891).
REFERENCIAS
[1]H. Arguello and G. R. Arce,
“Colored coded aperture design by concentration of measure in compressive
spectral imaging,” IEEE Transactions on Image Processing, vol. 23, no.
4, pp. 1896–1908, 2014.
[2]H. Rueda, H. Arguello, and
G. R. Arce, “Dmd-based implementation of patterned optical filter arrays for
compressive spectral imaging,” JOSA A, vol. 32, no. 1, pp. 80–89, 2015.
[3]K. Leon, L. Galvis, and H.
Arguello, “Reconstruction of multispectral light field (5d plenoptic function)
based on compressive sensing with colored coded apertures from 2d projections,”
Revista Facultad de Ingeniería Universidad de Antioquia, no. 80, Ene. 2016.
[4]A. Wagadarikar, N. P.
Pitsianis, X. Sun, and D. J. Brady, “Video rate spectral imaging using a coded
aperture snapshot spectral imager,” Optics Express, vol. 17, no. 8, pp.
6368–6388, 2009.
[5]C. Correa, D. F. Galvis,
and H. Arguello, “Sparse representations of dynamic scenes for compressive
spectral video sensing,” Dyna, vol. 83, no. 195, p. 42, 2016.
[6]K. Leon, L. Galvis, and H.
Arguello, “Spectral dynamic scenes reconstruction based in compressive sensing
using optical color filters,” in SPIE Commercial+ Scientific Sensing and
Imaging. International Society for Optics and Photonics, 2016, pp.
98600D–98600D.
[7]B. Pedraza, P. Rondon, H.
Arguello, “Sistema de reconocimiento facial basado en imágenes con color,” Rev.
UIS Ing., vol. 10, no. 2, 2012.
[8]A. B. Ramirez, H. Arguello,
and G. Arce, “Video anomaly recovery from compressed spectral imaging,” in Acoustics,
Speech and Signal Processing (ICASSP), 2011 IEEE International Conference on.
IEEE, 2011, pp. 1321–1324.
[9]J. Chen, Y. Wang, and H.
Wu, “A coded aperture compressive imaging array and its visual detection and
tracking algorithms for surveillance systems,” Sensors, vol. 12, no. 11,
pp. 14397–14415, 2012.
[10]
A. Banerjee, P. Burlina, and J. Broadwater, “Hyperspectral video
for illumination-invariant tracking,” in Hyperspectral Image and Signal
Processing: Evolution in Remote Sensing, 2009. WHISPERS’09. First Workshop on.
IEEE, 2009, pp. 1–4.
[11]
T. Goldstein, L. Xu, K. F. Kelly, and R. Baraniuk, “The stone
transform: Multi-resolution image enhancement and compressive video,” IEEE
Transactions on Image Processing, vol. 24, no. 12, pp. 5581–5593, 2015.
[12]
A. C. Sankaranarayanan, L. Xu, C. Studer, Y. Li, K. F. Kelly, and
R. G. Baraniuk, “Video compressive sensing for spatial multiplexing cameras
using motion-flow models,” SIAM Journal on Imaging Sciences, vol. 8, no.
3, pp. 1489–1518, Jul., 2015.
[13]
D. Reddy, A. Veeraraghavan, and R. Chellappa, “P2c2: Programmable
pixel compressive camera for high speed imaging,” in Computer Vision and
Pattern Recognition (CVPR), 2011 IEEE Conference on. IEEE, 2011, pp.
329–336.
[14]
C. Liu, “Beyond pixels: exploring new representations and
applications for motion analysis,” Ph.D. dissertation, Citeseer, 2009.
[15]
M. A. T. Figueiredo, R. D. Nowak, and S. J. Wright, “Gradient
projection for sparse reconstruction: Application to compressed sensing and
other inverse problems,” IEEE Journal on Selected Topics in Signal
Processing, vol. 1, no. 4, pp. 586–597, 2007.
[16]
A. Mian and R. Hartley, “Hyperspectral video restoration using
optical flow and sparse coding,” Optics express, vol. 20, no. 10, pp.
10658–10673, 2012.
[17]
F. Yasuma, T. Mitsunaga, D. Iso, and S. K. Nayar. 2008 CAVE
Projects: Multispectral Image Database.
[Online],Available:http://www.cs.columbia.edu/CAVE/databases/multispectral/
![]() −
− -norm
recovery algorithm than using conventional sensors, the reconstruction exhibits
diverse challenges originated by the temporal variable or motion. The motion
during the reconstruction produces artifacts that damages the entire data. In
this work, a multiresolution-based reconstruction method for compressive
spectral video sensing is proposed. In this way, it obtains the temporal
information from the measurements at a low computational cost. Thereby, the
optimization problem to recover the signal is extended by adding temporal
information in order to correct the errors originated by the scene motion.
Computational experiments performed over four different spectral videos show an
improvement up to 4dB in terms of peak-signal to noise ratio (PSNR) in the
reconstruction quality using the multiresolution approach applied to the
spectral video reconstruction with respect to the traditional inverse problem.