1

Methodology for the design of a thermal energy storage module for a

solar tunnel dryer using phase change materials (PCM)

Metodología para el diseño de un módulo de acumulación térmica usando materiales de cambio de fase (PCM) para un secador solar

de túnel

Mario Escobar-Ochoa¹, Sandra Cuervo-Andrade², Sonia Rincon-Prat³

¹Grupo de Investigación en Biomasa y Optimización Térmica de Procesos – BIOT, Facultad de Ingeniería, Departamento de

Ingeniería Mecánica y Mecatrónica, Universidad Nacional de Colombia - sede Bogotá, Colombia.

Email: maaescobaroc@unal.edu.co

²Grupo de Investigación en Desarrollo Tecnológico, Mecatrónica y Agroindustria- GiDeTechMa y Grupo de Investigación en

Biomasa y Optimización Térmica de Procesos – BIOT, Facultad de Ingeniería Mecánica, Universidad Pontificia

Bolivariana - seccional Bucaramanga, Colombia. Email: sandra.cuervo@upb.edu.co

³Grupo de Investigación en Biomasa y Optimización Térmica de Procesos – BIOT, Facultad de Ingeniería, Departamento de

Ingeniería Mecánica y Mecatrónica, Universidad Nacional de Colombia - sede Bogotá, Colombia. Email: slrinconp@unal.edu.co

ABSTRACT

The increasing interest in renewable energy has opened an opportunity to apply this technology in the industry and domestic sector. However, in solar-based systems, limitations associated with the intermittent energy delivery can cause unstable performance and unreliable designs. Weather fluctuations, such as wind speed and appearance of clouds, are considered the principal factors that contribute to the instability in the amount of energy available. In the agriculture, for instance, the use of thermal solar energy applied to dryer systems is highly desirable since the process

is energetically very intensive. Therefore, it is feasible to design dryer devices for agricultural products, with important economic returns due to energy savings and the value added to the materials processed. Thus, the energy performance of systems that operate with solar thermal energy can be improved by introducing an energy accumulation system based on the use of phase change materials (PCM). The detailed methodology for the design of a thermal energy accumulation system for a tunnel dryer type Hohenheim for agricultural products is presented. As PCM, paraffin is chosen because its melting temperature is near 60 °C, which is an appropriate value for the drying temperature of this kind of products. The theoretical calculations show that the value of the surface temperature has an important influence on phase change calculations and the total mass of PCM required in the system. On the other hand, the heat transfer is dominated by the external heat transfer in the air. Additionally, the tube diameter significantly affects the phase change time. The results obtained are important and make a significant contribution to the knowledge required for implementations of similar systems, since little has been explored in this field in regions where the weather conditions are suitable to unexpected changes. The design should be implemented in an experimental prototype of Hohenheim dryer and its performance is to be determined based on measurement of the energy change of the drying air.

KEYWORDS: Renewable energy; solar dryer; PCM; heat transfer.

RESUMEN

El creciente interés en las energías renovables ha abierto una oportunidad para aplicar esta tecnología en la industria y el sector nacional. Sin embargo, en sistemas basados en energía solar, las limitaciones asociadas con la entrega de energía intermitente pueden causar un rendimiento inestable y diseños poco confiables. Las fluctuaciones climáticas, como la velocidad del viento y la apariencia de las nubes, se consideran los principales factores que contribuyen a la inestabilidad en la cantidad de energía disponible. En la agricultura, por ejemplo, el uso de la energía solar térmica aplicada a los sistemas de secado es altamente deseable ya que el proceso es energéticamente intensivo. Por lo tanto, es factible diseñar dispositivos de secado para productos agrícolas, con retornos económicos importantes debido al ahorro de energía y al valor agregado de los materiales procesados. Por lo tanto, el rendimiento energético de los sistemas que funcionan con energía solar térmica se puede mejorar mediante la introducción de un sistema de acumulación de energía basado en el uso de materiales de cambio de fase (PCM). Se presenta la metodología detallada para el diseño de un sistema de acumulación de energía térmica para un secador de túnel tipo Hohenheim para productos agrícolas. Como PCM, se elige parafina porque su temperatura de fusión es cercana a 60 ° C, que es un valor apropiado para la temperatura de secado de este tipo de productos. Los cálculos teóricos muestran que el valor de la temperatura superficial tiene una influencia importante en los cálculos de cambio de fase y la masa total de PCM requerida en el sistema. Por otro lado, la transferencia de calor está dominada por la transferencia de calor externa en el aire. Además, el diámetro del tubo afecta significativamente el tiempo de cambio de fase. Los resultados obtenidos son importantes y aportan una contribución significativa al conocimiento requerido para implementaciones de sistemas similares, ya que se ha explorado poco en este campo en regiones donde las condiciones climáticas son adecuadas para cambios inesperados. El diseño debe implementarse en un prototipo experimental de secador Hohenheim y su rendimiento debe determinarse en función de la medición del cambio de energía del aire de secado.

PALABRAS CLAVE: Energía renovable; secador solar; PCM; transferencia de calor.

INTRODUCTION

The use of direct sun energy as renewable source in the industrial and domestic sector is limited due to its intermittent delivery. Particularly in the tropical region the availability of light hours is greater compared to the areas between the Arctic and Antarctic polar circles and the Tropics of Cancer and Capricorn. This favors the use of devices powered by this type of energy. Therefore, it is necessary to know the potential of renewable energy sources in the region, to make a good design process in projects related to this type of technologies [21,22].

However, weather fluctuations (winds, clouds, etc.) cause variation in the amount of energy entering the devices. For this reason, mechanisms have been proposed to improve the conditions of stability and reliability of solar based systems. Such is the case of the use of thermal energy accumulation systems, using phase change materials (PCM), applied to devices that operate using solar thermal energy. Current research is aimed at comparing different types of PCM, determining the most appropriate depending on the application that is required. The most common uses, taking advantage of solar thermal energy can be found in applications for heating enclosures or swimming pools, water heaters or for dehydrating products [1, 2, 3].

In the value chain for agricultural products, drying is the process with the highest energy requirement. For that reason, the implementation of dryers that use solar thermal energy has advantages, such as energy savings and reduction of production costs, together with increase in the value added of the products and reduction in product losses for farmers. In developing countries product losses can account for 30 % to 40 % of harvested material [4].

The main advantage of thermal energy accumulation systems using PCM in drying applications, compared with sensible heat accumulation, is that it is possible to maintain a constant temperature inside the drying chamber during energy delivering by phase change.

In the present work, the methodology of design of a thermal energy accumulation system for a Hohenheim type solar tunnel dryer for aromatic plants is presented.

The methodology includes the analysis of the heat transfer phenomena involving natural convection during phase change in the PCM and forced convection in the drying air. Paraffin is used as PCM as it has a melting temperature of 60 ˚C which is in the appropriate range for the drying of aromatic plants. Other factors such as cost, availability and safety were also considered. The modified tunnel dryer, has a modular design consisting of three main parts: the collector, the accumulation system and the drying chamber. The designed accumulation system consists of a cross flow heat exchanger. The PCM is located inside copper tubes that are located perpendicular to the direction of the air flow. It was observed that the surface temperature of the tube has an important effect on the phase change time and on the total mass of PCM required in the system. On the other hand, a greater thermal resistance is presented in the heat transfer process by external convection, compared to the internal one. The developed methodology and the results obtained are important and make a significant contribution to the knowledge for possible implementations of similar systems since little has been explored in this field in the tropical region.

INITIAL CONSIDERATION

The energy accumulation module is designed to be placed in a Hohenheim-type tunnel dryer between the collector and the drying chamber. The basic configuration of this type of dryer can be found elsewhere [5, 6, 7, 8, 9]. The drying air is forced to flow through the dryer by means of fans located at the initial part of the collector. In the collector, the drying air is heated and then is conducted through the accumulation system and finally through the drying chamber.

The accumulation system consists of copper tubes in a tube bank arrangement forming a cross-flow heat exchanger. In the solar collector, the energy coming from

the sun is captured by means of radiation heat transfer in a black surface and then transferred through convection to the drying air. When a suitable level of radiation is available, air flows through the system and is heated at a higher temperature than the melting temperature of the paraffin. Then by passing the accumulation system the paraffin inside the tubes undergoes melting. The design of the heat exchanger requires the quantification of the heat transfer phenomena that occur inside the tubes (natural convection with phase change) and outside of them (external forced convection). For the calculations following assumptions are made:

• The design is performed for the option in which the system is accumulating energy, the PCM undergoes a melting process. After having designed the system, its behavior during solidification is analyzed.

• No overheating of the melted PCM or sub cooling of the solidified PCM is considered.

• The inlet temperature and mass flow of the air in the heat exchanger is constant.

• Energy transferred in the system during phase change varies with time due to the continuous changing of the solid and melting fractions inside the tubes. For design purposes the heat transfer in the system is analyzed as a steady state process with average constant parameters.

• Heat losses in the system are negligible.

From the last assumption an energy balance in the module states that the energy delivered by the air is transferred to the phase change material during the phase change process. This quantity of energy is the parameter that enables to determine whether the heat exchanger meets the established requirement for desired heat transfer rate (_d) or not. The desired heat transfer rate is calculated from the temperature change in the air based on an input temperature in the tube bank of (𝑇₀= 65 °C) (temperature reachable at the collector outlet) and the desired outlet temperature 𝑇_F= 60 °C (suitable drying temperature for agricultural products [11]) and can be

calculated using (Equation 1).

_d = 𝑚̇𝐶p,aire @T_prom(𝑇₀- 𝑇_F) (1)

The air velocity is set at 𝑢 = 0.8 m s^-1, this value lies inthe higher range used in this type of dryers [3]. Higher velocities mean higher air mass flows and consequently the heat transfer requirement to reach the desired temperature is higher, the module is than designed for this work condition. The thermo physical properties of air are calculated at the average temperature (T_prom) between inlet () and outlet (𝑇_F).

For calculation purposes, all tubes were assumed to have the same length of 1 m corresponding to the width of the

tunnel dryer. However, the tubes have different dimensions, since this system is incorporated in a module with the same geometry of the solar dryer in gable roof disposition. This can be seen in Figure 7 were the length of each tube decreases with the vertical distance. The final design considers these variations by increasing the number of rows at the end of the assembly in a way that the heat transfer area 𝐴_T and the mass of PCM correspond to the calculated values.

METHODOLOGY

The design methodology comprises four main stages. Stage one includes heat transfer through phase change inside the tubes. The paraffin properties required to perform the calculations are summarized in Annex A1. The analysis of this zone allows the calculation of the convection heat transfer coefficient on the internal side ℎ_int and the required minimum mass of PCM required. Stage two corresponds to the geometric sizing of the system, which is based on the required minimum mass of PCM and the available space in the cross section of the tunnel. The dimensioning allows determining the convection heat transfer coefficient in the external side ℎ_ext of the tubes. The calculation procedures of ℎ_in and ℎ_ext requires the knowledge of the surface temperature of

the tubes (𝑇_s). As this parameter is not known a first estimation is made. With ℎ_int and ℎ_ext, the total heat transfer coefficient of the exchanger U is determined.

Stage three, includes verifying if the proposed design meets the requirement given by the desired heat _d This

is done by applying the Number of Transfer Units (NTU)

method for the design of heat exchangers. The effectiveness of the heat exchanger and the actual heat transfer _real, which must be greater than or equal to _d, were calculated. In case of not fulfilling the condition, a

geometric resizing of the system was carried out. When the heat requirement is fulfilled, the actual surface temperature 𝑇_s of the tubes and the final temperature 𝑇_Fof the air are calculated in stage four. Finally, in stage five, the design is consolidated.

Analysis of heat transfer inside the tubes

For the heat transfer analysis inside the tubes the correlations proposed by Bareiss et al. [8] are used. They developed expressions for an average Nu_int (Equation 2)

and an average dimensionless melting time 𝜏_𝑎 (Equation 3) for a PCM inside a circular enclosure. The average value of ℎ_int is calculated from Nu_int as ℎ_int= Nu_int 𝑘_𝑃𝐶𝑀/𝑟_𝑖𝑛𝑡. Using (Equation 4) together with (Equation 5 and 6) the required minimum mass of PCM in the system can be determined.

(2)

(3)

(4)

(5)

(6)

External heat transfer through the tubes

The analysis of the heat transfer on the external side of the heat exchanger is based on the method proposed by Zukauskas presented by Cengel [9]. For a staggered configuration Nu_ext can be estimated according to (Equation 7). is calculated using the maximum air speed in the arrangement. is determined from as =Nu_ext /. The overall heat transfer coefficient of the exchanger (U) is calculated according to (Equation 8).

(7)

(8)

Determination of the heat capacity of the module

Using the calculated external and internal heat transfer coefficients, the heat transfer capacity of the module is determined using the method of Number of Transfer Units (NTU-Method) [11, 10]. The actual heat transfer in the module is calculated according to (Equation 9 to 11).

The maximal heat transfer is calculated from the maximum temperature difference and the heat capacity of the air .

In the case that it is necessary to perform a resizing process to increase .

Determination of the actual tube surface temperature 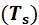and air exit temperature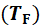

The procedure for calculating the actual tube surface temperature was to relate the to find the phase change time by (Equation 6). Initially the assumed is taken to find the mass of PCM (. That calculated time is compared to the time that is calculated when the phenomenon of heat transfer into the tubes is involved. So, the actual tube surface temperature () is when this iterative process is performed, and equalities are achieved at the time of phase change.

𝑇_F is calculated using Equation 9 [6] from an energy balance of the drying air.

(9)

RESULTS AND DISCUSSION

Table 1 show the results of the heat transfer analysis inside and outside the tubes respectively when using a first set of given conditions. Table 2, shows the results of the operation of the heat exchanger.

For the analysis of the external heat transfer the staggered configuration was used as it allows a higher turbulence in the air increasing the heat transfer in the system. The distances between tube axes are initially fixed as two times the diameter of the tube. Table 3 presents the main dimensions of the tube bank.

Table 1. Calculated heat transfer parameters.

Parameters	Value
Internal heat transfer
[-]	0.01166
Nu_int[-]	48.77
	561.35
	64.74
Fo [-]	1.77
𝑡 [min]	126.80
External heat transfer
Nu_ext[-]	41.16
	28.22

Source: Own elaboration.

(10)

(11)

(12)

Table 2. Calculated parameters of the heat exchanger.

Parameters	Value
U [W m-2 K-1]	26.87
∆ [°C]	5.50
[W]	1 769.07
NTU [-]	0.79
𝜀 [-]	0.55
[W]	966.83
[W]	1 608.24

As can be seen from Table 2 the calculated value of is lower than . Therefore, it is necessary to perform a resizing of the system aiming to increase the value of . As shown in (Equation 10) this value is a function of the effectiveness 𝜀 and the maximum heat .

The value of , for the present study, is considered constant, since it depends on that in turn depends on the specific heat of the air and its mass flow and Δ is a design parameter. To reach the desire value of = 1 608.24 an effectiveness 𝜀 of 90.90 % should be needed, representing an increment of 63 % from the initial value of 55,00 %. NTU must be then incremented from 0,79 to 2.377, calculated from (Equation 11). As shown in (Equation 12) the value of NTU can be increased by:

· Increasing the overall heat transfer coefficient U.

· Increasing the heat transfer area .

· A simultaneously increase in U and (in case the increase of one of the two independently is not sufficient to achieve the expected NTU value).

Table 3. Configuration of the tube bank.

Scheme	Parameters	Value
	Total mass of PCM required in a tube () [kg]	0.90
	Number of tubes	73
	S_T [m]	0.083
	A₁ [m²]	0.083
	A_T [m²]	0.0413
	S_L [m]	0.083
	S_D [m]	0.0923
	A_D [m²]	0.051
Source: Own elaboration.

Source: Own elaboration.

Figure 1. Variation of the overall heat transfer coefficient U with respect to and .Source: Own elaboration.

The overall heat transfer coefficient U depends on and . In Figure 1 the change of U is presented with a variation of (line with asterisks) keeping the value of constant in 28.22 W m^-2 K^-1; and with a variation of (line with circles) keeping the value of constant at 561.35 W m^-2 K^-1. It is clearly observed that the system is dominated by the external heat transfer. This behavior is expected because of the high value of the internal heat transfer coefficient, compared to the value of the external heat coefficient. Modifications tending to increase the value of U should concentrate on improving the heat transfer from the external side.

An increase in is reached with an increase in which is achieved by increasing and making the ratio / greater than 1 as expected from Equation 7.

A decrease in and increases the maximum air velocity in the tube bundle making higher.Figure 2 shows the variation of with /. The variation is done by keeping the value of constant at 0.05159, which corresponds to 2.5 times the radius of the tube (0.0206m) varying the value of according to the desired ratio. This figure shows that with an increase in the ratio / the decreases considerably. This is because the decrease in the Reynolds number (indicated in the figure) caused by the increase in the distance has a greater effect on Equation 7 than the increase in that ratio. The pressure drop in the tube bank is determined by applying the relationship developed by Zukauskas et al. [14, 15]. The calculated pressure drop is only 60 Pa for the most critical case in which and are low, so it is not considered a relevant issue when selecting the distances between tubes.

Figure 2. Variation of with the relation /. is included for selected values. Source: Own elaboration.

Figure 3 presents the results of U by / 1.0 and 1.2. The best option to implement in the design is / 1.0, with a distance between centers of 1.25D, obtaining U= 44.99 W m^-2 K^-1 that corresponds to an increment of 59.71% when compared with the initial value.

Figure 3. Overall heat transfer coefficient U by / 1.0 and 1.2. Source: Own elaboration.

Another possibility to increase the value of U is by changing the tube diameter. Two possibilities where studied maintaining a relation =. This distance, was proposed by Holman [12]. The effect of varying the tube diameter affects both the inside and the outside heat transfer conditions of the tubes, so this is considered when calculating U. As can be seen in Figure 4 with an increment in tube diameter (these are the commercial ranges of pipelines) the overall heat transfer coefficient is considerably affected. Between and 1.5 in of commercial diameters. However, for pipes with a diameter between 2 and 4, there is no significant variation in the overall heat transfer coefficient, therefore, no account will be taken.

Figure 4. Behavior of U varying the nominal of the copper tube. Source: Own elaboration.

Due to the increment of the cross section of the tubes, the phase change time increases as the radius becomes larger. Phase change time is an important design parameter as short phase change times mean short energetic autonomy of the system. For the present project 2 h autonomy is considered as acceptable. It was observed that diameters smaller than 1.5 in are not suitable for the design because they have a shorter phase change time. In turn, large diameters have a lower overall heat transfer coefficient value.

When performing the calculations again, with the nominal diameter of 1.5 in, / ratio and distance; the new values are: = 48.91 W m^-2 K^-1, NTU =1.32, 𝜀 = 0.73, = 1298.33 W. Although, approaches , it is still below it.

Another improvement in NTU can be reached by increasing the heat transfer area . Figure 5 presents the variation of NTU with between 9.47 and 12.45 m², which is the range of area that can be handled in the system. As shown in Figure 5, the increment in NTU is not as effective as when increasing U. Moreover, the possibility of increasing the heat transfer area of the tubes is limited due to space considerations, structural problems that can be presented in the module due to excessive weight and increasing costs. Consequently, an increment in heat transfer area is not considered.

Table 4 presents a general summary of the resizing of the system. With these changes, the ratio of and is 80.73 %. The value of 1298.33 W is the maximum achievable heat transfer in the system and is accepted for the final design. Finally, the Table 5 shows the actual values of and compared with the values assumed initially.

Figure 5. NTU behavior, modifying 𝐴T. Source: Own elaboration.

Table 4. Design parameters recalculated with ==1.25D.

Parameter	Value
[W K^-1]	321.65
∆𝑇_máx [°C]	5.50
[W]	1769.07
NTU [-]	1.32
𝜀 [-]	0.73
[W]		1 298.33

Source: Own elaboration.

Table 5. Assumed and calculated values of 𝑇s and 𝑇F.

Temperature	Assumed value	Calculated value
T_s [°C]	59.50	59.38
T_F [°C]	60.00	60.96

Source: Own elaboration.

With the calculated 𝑇_s (59.38 ° C) and the 𝑇_s assumed initially, Table 6 shows a comparison of parameters calculated from the point of view of the phenomenon of internal heat transfer in the tube. As can be seen in Equation 7, the incidence of 𝑇_s in the external phenomenon of heat transfer is only evident in the ratio of (Pr/Pr_𝑠)^0.25, whereby it can be stated that the temperature of the surface, has no relevant impact on the external heat transfer. A different situation occurs in the internal side, where 𝑇_s plays an important role when calculating the time of phase change and minimum mass of PCM.

Table 6. Comparison of internal heat transfer parameters with calculated and assumed T_s

Parameters to evaluate	Value with 𝑇_s assumed (59.50 °C)	Value with𝑇_s calculated (59.38 °C)
Dimensionless time 𝜏_𝑎[-]	0.01166	0.01089
Nusselt Nu [-]	48.77	52.23
Minimum mass of PCM [kg]	64.74	80.19
Fourier Fo [-]	1.77	2.19
Phase change time 𝑡 [min]	126.80	157.07

Source: Own elaboration.

FINAL DESIGN

Figure 6 shows the final configuration of the thermal storage module. As can be seen in figure 7a, the length of the tubes varies with the vertical distance, therefore, it is necessary to attach more rows in the module, to maintain the calculated heat transfer area of 9.47 m². Figure 7b shows the configuration of the rows along the accumulation module. This final design will be implemented in a prototype of a Hohenheim-type tunnel dryer to evaluate its performance experimentally.

(b)

Figure 6. Final configuration of the thermal storage module. (a) Cross section (b) Longitudinal section. Measures in meters. Source: Own elaboration.

PERFORMANCE OF THE SYSTEM AT SOLIDIFICATION CONDITIONS

Using the above design, the performance of the thermal storage module during solidification conditions is analyzed. In this case the inlet temperature is lower than the phase change temperature of the paraffin. It is assumed that the PCM is in liquid phase at the phase change temperature and it is instantly subjected to the air temperature. For the analysis, only the latent heat is considered. Applying the NTU-Method the actual heat transfer in the system is calculated and presented in Table 7 for different air temperatures.

Table 7. Results applying the NTU-Method.

𝑇₀ [°C]		𝐶_mín	NTU	𝜀
20	13 461.21	345.16	1.242	0.7112
25	11 665.68	343.11	1.245	0.7119
30	9 895.10	341.21	1.251	0.7139
35	8 108.96	337.87	1.259	0.7162
40	6 388.77	336.25	1.265	0.7177
45	4 641.51	331.54	1.277	0.7213
50	2 968.68	329.85	1.282	0.7225
55	1 310.23	327.56	1.286	0.7239

Source: Own elaboration.

Analyzing the behavior of the system, varying 𝑇₀, in terms of heat transfer, there is no significant variation, so that U and NTU are maintained in similar values. However, what makes difference, is the difference in temperature that is reflected in the calculation of and . In these parameters if a change is observed, so they are in function of the temperature difference.

Figure 7 shows the variation of 𝑇_F and with 𝑇₀. As the effectiveness remains almost constant is proportional to and consequently to 𝑇_F- The minimum outlet temperature for an inlet temperature of 20 °C is 48 °C which is an acceptable drying temperature. Furthermore, at higher heat transfer rates lower phase change times are expected, since the total amount of energy remains constant as it depends on the mass of PCM.

Figure 7. Behavior of the system, and 𝑇_F varying 𝑇₀. Source: Own elaboration.

The phase change time can be calculated from Equation

13. is determined as the total energy that the mass of PCM delivers during solidification (for the purposes of this analysis the sensible heat is not considered).

(13)

As shown in Figure 8 as decreases the phase change time increases considerably. Thus, if the temperature in the system drops instantaneously from phase change temperature to ambient temperature (20 °C) the system has still autonomy of approximately 30 min. If the temperature remains at 55 °C the autonomy would rise to more than 4.6 h.

Figure 8. Variation of phase change time t [min]with 𝑇_0. Source: Own elaboration.

CONCLUSIONS

One of the main disadvantages of implementing drying devices using solar energy is the intermittent energy supply due to weather fluctuations. This can be reduced with the implementation of thermal energy storage systems using PCM materials.

The developed methodology for the design of an energy storage module consisting of a cross flow heat exchanger in which the PCM is located inside the tubes can be easily implemented in the design of modules with different conditions of temperature and air flow. The analysis of the heat transfer phenomena showed that the system is controlled by the external heat transfer in the air which is strongly affected by the air speed in the system.

The heat transfer during phase change inside the tubes is important in determining the melting time which depends strongly on the surface temperature and the tube diameter. Melting times from 30 min to 4.6 h can be achieved depending on the outside temperature.

ACKNOWLEDGMENTS

The authors gratefully acknowledge the financial support by the Vicerrectoría de Investigación of the Universidad Nacional de Colombia (Hermes 19926) and the Universidad Pontificia Bolivariana of Bucaramanga.

Appendices

Appendix A

Table A1. Thermophysical Properties of Semi-Defined Paraffin

Properties	Value	References
𝑇_PCM[˚C]	59.00	[13]
𝐶_p,sól [J kg^-1 K^-1]	59 000.00	[14]
𝐶_p,líq [J kg^-1 K^-1]	2 490.00	[14]
𝜌_sól [kg m^-3]	893.00	[14]
𝜌_líq[kg m^-3]	782.00	[14]
𝜌′	0.88	[15]
𝑘_PCM [W m^-1 K^-1]	0.22	[16]
𝜆 [J kg^-1]	189,000	[14]
𝛼_líq [m² s^-1]	8.50.E-08	[17]
𝛽 [K^-1]	7.78.E-04	[18]
𝜈 [m² s^-1]	5.23.E-06	[18]
𝜇 [kg m^-1 s^-1]	4.84.E-03	[18]

Symbol	Definition	Symbol	Definition
𝛼_líq	Thermal diffusivity of liquid PCM [m² s^-1]	𝜇	Dynamic viscosity of liquid PCM [kg m^-1 s-1]
𝛽	Coefficient of thermal expansion of PCM [K^-1]	𝜈	Kinematic viscosity of liquid PCM [m² s^-1]
∆𝑃	Pressure drop [Pa]	𝜌′	Liquid / solid density ratio of PCM [-]
∆𝑇_𝑚_á_𝑥	Maximum temperature difference [K]	ρ_líq	Liquid state density of PCM [kg m^-3]
𝜀	Effectiveness [-]	ρ_sól	Solid state density of PCM [kg m^-3]
𝜆	PCM Latent heat of fusion [J kg^-1]	𝜏_𝑎	Dimensionless of time [-]

Greek alphabet

Nomenclature

Latin alphabet

Symbol	Definition	Symbol	Definition
Ar	Number of Archimedes [-]	Nu_D	Number of Nusselt abroad[-]
𝐴_T	Total area [m²]	NTU	Number of transfer units[-]
𝐴_TC	Heat Transfer Area [m²]	Pr	Prandtl number [-]
𝐴_TD	Total duct area[m²]		Desired heat flow [W]
C	Constant [-]		Maximum heat flow [W]
𝐶p,aire	Specific Heat of Air [J kg^-1 K^-1]		Real heat flux [W]
𝐶_p,líq	Specific heat in the liquid state of PCM[J kg-1 K-1]	Ra	Rayleigh number [-]
𝐶_p,sól	specific heat in the solid state of PCM[J kg-1 K-1]	Re	Reynolds number [-]
𝐷_int	Inner tube diameter [m]	𝑟_ext	External tube radius [m]
𝐷_ext	Outer tube diameter [m]	𝑟_int	Inner tube radius [m]
ƒ	Friction Factor [-]	Ste	Stefan number [-]
Fo	Fourier Number [-]	t	Phase change time [s]
𝑔	Gravity force [m s^-2]	𝑇_F	Final air temperature [K]
Gr	Grashof Number [-]	𝑇PCM	PCM Phase Change Temperature [K]
ℎ_ext	External Heat Transfer Coefficient [W m¹ K^-1]	𝑇_prom	Average temperature between initial and final[K]
ℎ_int	Internal heat transfer coefficient [W m^-1 K^-1]	𝑇_s	Tube surface temperature [K]
𝑘_cobre	Copper thermal conductivity [W m^-1 K^-1]	𝑇₀	Initial air temperature [K]
𝑘_PCM	PCM thermal conductivity[W m^-1 K^-1]	𝑢	Air speed [m s^-1]
𝑚_PCM	Minimum mass of PCM required in the system [kg]	U	Overall heat transfer coefficient [W m^-1 K^- ¹]
𝑚_t	Mass of PCM in a tube [kg]	𝑢_máx	Maximum air speed [m s^-1]
𝑚̇_a	Air mass flow [Kg s^-1]		Air flow [m³ s^-1]
N	Tubes number [-]	𝑉ġ	Volumetric expenditure [m³ s^-1]
𝑁_L	Tubes number in cross section[-]	𝑉_tubo	Tube volume [m³]
Nu	Nusselt number [-]	vent	Fan Power [W]
		X	Correction factor [-]

REFERENCES

[1] Mustayen A G M B, Mekhilef S and Saidur R Performance study of different solar dryers: A review Renew. Sustain. Energy Rev. vol.34, pp. 463–70, Jun, 2014.

Mekhilef S, Faramarzi S Z, Saidur R and Salam Z “The application of solar technologies for sustainable development of agricultural sector Renew.” Sustain. Energy Rev. vol.18, pp. 583–94, Dec, 2013.

Tiwari G N, Bhatia P S, Singh A K and Sutar R F “Design parameters of a shallow bed solar crop dryer with reflector.” Energy Conversion. Management. vol. 35, no. 6, pp. 535–42, Jun, 1994.

Karim M A. and Hawlader M N A. “Development of solar air collectors for drying applications.” Energy Conversion. Management. vol. 45, no. 3, pp. 329–44., Feb, 2004.

García P, Rincón S and Cuervo S. “Implementación del secador solar de túnel tipo Hohenheim en productos agrícolas, Revisión de literatura.” Rev. Puente, vol. 10 no. 1, pp. 7–19. 2016.

Hossain M A. and Bala B K. “Drying of hot chilli using solar tunnel drier.” Sol. Energy Rev. vol. 81, pp. 85– 92, Jan, 2007.

Bala B K, Morshed M A and Rahman M F. “Solar drying of mushroom using solar tunnel dryer.” Int. Sol. food Process. Conf. 1–11. 2009

Hossain M A, Woods J L and Bala B K. “Optimisation of solar tunnel drier for drying of chilli without color loss.” Renew. Energy Rev. vol. 30, no. 5, pp. 729–742, Apr, 2005.

Hensel O and Esper A. “The Hohenheim solar tunnel dryer-20 years of succes Food Chain.” Int. J. small scale food processing, vol. 31, pp. 2–27, 2001.

Bareiss M and Beer H. “An analytical solution of the heat transfer process during melting of an unfixed solid phase change material inside a horizontal tube” Int. J. Heat Mass Transf. vol. 27,no. 5, pp. 739–46, May, 1984.

Çengel Y. “Heat and mass transfer: A practical approach ed McGraw-Hill.” Boston: Boston: McGraw-Hill, cop. 2007.

Thulukkanam K. “Heat exchanger design handbook ed CRC Press.” Boca Raton, Florida: Taylor & Francis Group, LLC, 2013.

Žukauskas A and Ulinskas R, “Efficiency Parameters for Heat Transfer in Tube Banks.” Heat Transf. Eng. vol. 6, no. 1, pp. 19–25. Oct, 1985.

Holman J. “Heat Transfer ed B Stenquist, New York: Raghothaman Srinivasan.” 2010.

Oliver A, Neila F J and García-Santos A. “Clasificación y selección de materiales de cambio de fase según sus características para su aplicación en sistemas de almacenamiento de energía térmica” Mater. Construcción, vol. 62, pp.131–40, Ene-Mar, 2012.

Sari A and Karaipekli A. “Thermal conductivity and latent heat thermal energy storage characteristics of paraffin/expanded graphite composite as phase change material Appl.” Therm. Eng. vol. 27, no. 8-9, pp. 1271–1277, Jun, 2007.

Ukrainczyk N, Kurajica S and Šipušié J. “Thermophysical Comparison of Five Commercial Paraffin Waxes as Latent Heat Storage Materials Chem.” Biochem. Eng. Q. vol, 24, no. 22, pp. 129–37, Jul, 2010.

Py X, Olives R and Mauran S. “Paraffin/porous-graphite-matrix composite as a high and constant power thermal storage material” Int. J. Heat Mass Transf. vol. 44, no. 14, pp. 2727–2737, Jul, 2001.

Himran S, Taraka R and Duma A “An Analysis on Thermal Energy Storage in ParaffinWax Using Tube Array on a Shell and Tube Heat Exchanger.” Int. J. Mech. Aerospace, Ind. Mechatron. Manuf. Eng. vol. 9, no. 10, pp. 1781–8, 2015.

Prasad A. and Sengupta S. “Nusselt number and melt time correlations for melting inside a horizontal cylinder subjected to an isothermal wall temperature condition.” J. Sol. Energy Eng. vol. 110, no.4, pp. 340–345, Feb, 1988.

Vergara Barrios P. P., Rey López J. M. Osma Pinto G. A. and G.Ordóñez Plata, “Evaluación del potencial solar y eólico del campus central de la Universidad Industrial de Santander y la ciudad de Bucaramanga, Colombia,” Rev. UIS Ing., vol. 13, no. 2, pp. 49–57, 2014.

C A Díaz Gonzalez, López N, Gélvez Arocha O and J L. Chacón Velasco, “Diseño y construcción de una planta piloto para la producción de biodiesel de manera continua,” Rev. UIS Ing. vol. 7, no. 1, pp. 105–133, 2008.