INTRODUCCIÓN

La fluidización es la tecnología donde se pone en contacto un lecho de sólidos con un flujo de fluido, como resultado, las partículas sólidas en cierto momento, alcanzan un comportamiento similar al de un fluido. Los reactores de lecho fluidizado son tecnologías importantes para operaciones heterogéneas de gas-sólido en la industria petroquímica, desde aplicaciones catalíticas [1] y procesos no catalíticos [2]. Las aplicaciones industriales más importantes incluyen craqueo catalítico, combustión de carbón y biomasa. Uno de los tipos más relevantes de reactor de lecho fluidizado es el reactor de flujo ascendente, que también se conoce como riser y el de flujo descendente o Downer. Datos históricos indican que, desde 1926, se utilizaron procedimientos de lecho fluidizado para la gasificación del carbón.

Las primeras unidades se encuentran en Alemania y Japón. En 1936, la primera unidad de craqueo catalítico industrial en un lecho fijo entró en funcionamiento, conocido como proceso de Houdry. El proceso era semi-continuo y consistió en tres o cuatro reactores que contenían arcilla tratada (SiO₂-Al₂O₃). [3]–[5]. Debido a la necesidad de gasolina para aviación durante la Segunda Guerra Mundial, el gobierno de Estados Unidos emitió una ley, donde exigía a las grandes compañías petroleras unir su conocimiento y esfuerzo para crear tecnologías de refinación de crudo, es aquí donde se crea los inicios del craqueo catalítico en lecho fluidizado o FCC (Fluid catalytic cracking), que entró en vigor el 25 de mayo de 1942 en la refinería de la Standard Oil (Esso - actual Exxon Mobil Corporation) Bateau Rouge (Lousiana-USA) y la primera unidad de craqueo en lecho móvil o Thermofor Catalytic Cracking TCC [6].

En 1959, se presenta el primer reactor de lecho fluidizado multi-etapa, donde el flujo de catalizador y gas, fluyen en contracorriente [7]. Otras aplicaciones, ventajas y desventajas de estos tipos de reactores de lecho fluidizado pueden ser estudiados en varias publicaciones [8]–[11]. Los reactores riser tienen una distribución no uniforme de los tiempos de residencia para los sólidos, además de una distribución no homogénea en la dirección radial, estos diferentes tiempos de contacto entre el gas y fases sólidas genera en ocasiones retromezcla de catalizador dando lugar a sobre-caqueo y una reducción en la selectividad [9], [12].

Las primeras investigaciones sobre flujo gas-sólido y mesoescalas fueron desarrolladas en el City College de Nueva York [13], en Inglaterra [14], [15], el Instituto de Institute of Gástechnology (IGT) en Chicago y en Francia [16], donde encontraron un comportamiento fluido-dinámico gas-sólido en riser de dos regiones características, una región densa (core) y una diluida (annulus), debido a que los sólidos forman aglomerados que se comportan como partículas grandes. La Figura 1 muestra un perfil de velocidad presentado por Miller & Gidaspow [17], los sólidos son transportados hacia arriba por el centro del riser (annulus) y descienden por las paredes (core); quedando el centro diluido. Para que las partículas puedan ser transportadas ascendentemente por riser, la caída de presión axial debe ser mayor que el peso de la región diluida. En las paredes existe una espesura radial gruesa.

El peso de la región anular debe ser inferior a la caída de presión axial de esta forma desciende lentamente. El núcleo es generalmente más amplio en la parte inferior de la columna que en la cima. Hay recirculación interna.

Figura 1. Perfil de velocidad sólidos en partículas FCC con 75μm de diámetro. Adoptado de Miller & Gidaspow [17]

Es muy importante definir el comportamiento fluido-dinámico de los lechos fluidizados para definir diseños cuando estos son aplicados a reacciones como en el caso del craqueo catalítico.

En este trabajo se utilizó dinámica de fluidos computacional (CFD) para describir el comportamiento de las fases sólida y gaseosa. CFD es una técnica que aplica y resuelve las ecuaciones de conservación [18] de masa y energía junto con modelos de turbulencia (k-e, k-w, SST, LES). Se empleó Large Eddy Simulation (LES) como metodología para describir las escalas turbulentas: LES fue desarrollado y aplicado inicialmente al flujo de gas que fluye sobre la superficie sólida y en los modelos atmosféricos [19]–[21], las escalas turbulentas más grandes (remolinos) aparecen lejos de la superficie sólida; los remolinos más pequeños son visibles cerca de la pared. Por esta razón se recomienda en la literatura [22] realizar una malla de refino cerca de la pared para captar estas estructuras más pequeñas tal como se muestra en la

Figura 2, no obstante, en este trabajo se propone una metodología de volúmenes de malla cuasi-.uniforme con Simulación de Grandes Escalas.

MATERIALES Y METODOLOGÍA APLICADAS

El lecho fluidizado utilizado fue tomado de Mathiesen, elegido debido a que su tamaño a escala de laboratorio y a los datos experimentales de velocidad y fracción volumétrica de sólidos presentados. Para la construcción de la geometría en 3D fue utilizada una Herramienta CAD (ICEM CFD) y se muestra en la Figura 3.

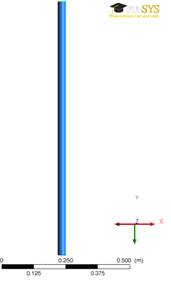
Figura 3. Geometría del lecho fluidizado adaptado de [23]

El lecho fluidizado tiene las siguientes características: diámetro interno de 0,032 m; altura de 1,0 m. Para llevar a cabo los cálculos, el flujo de aire se consideró a la temperatura y presión ambiente para tres velocidades del gas: 0,36 y 1,42 m / s, y una altura inicial de 0,05 m de lecho de sólidos y fracción volumétrica de 0,63.

Relación de escala y mallado

Normalmente se utiliza una malla no estructurada con el espaciado de cuadrícula uniforme; para el caso de un sistema de dos fases, se recomienda tener refinamiento en todo el dominio de control; debido a la interacción de las dos fases que forman diferentes estructuras turbulentas (remolinos) con diferentes órdenes de magnitud. La malla no uniforme con amplio espacio entre celdas proporciona una descripción incompleta de la malla y la resolución de la turbulencia, inestabilidad numérica y divergencia. En la práctica es difícil generar el tamaño de malla de la refinación que es proporcional (localmente) a la escala de la longitud de la turbulencia, D, la Figura 4 muestra las diferentes escalas que pueden ser analizadas en un reactor de craqueo catalítico circulante.

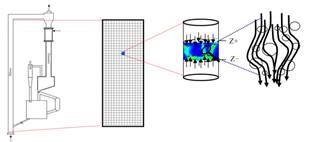
Figura 4. Diagrama esquemático del reactor FCC (izquierda a derecha): el equipo experimental, subdividido dominio (macro-escalas), diferencial de volumen que contiene la meso-escala y micro-escalas.

En flujos turbulentos, la escala espacial máxima o máxima escala de un vórtice se conoce como escala de longitud completa L (macro escala), y se determina por la dimensión característica del problema en cuestión. La disipación viscosa de energía contenida en un vórtice aumenta cuando el tamaño de vórtice disminuye. La dimensión más pequeña de un vórtice en un flujo turbulento se llama la escala de longitud de Kolmogorov, h, y la escala de tiempo asociado con este vórtice se llama la escala de tiempo de Kolmogorov, t dada por las siguientes ecuaciones:

Donde, n es la viscosidad cinemática turbulenta, y e es la tasa de disipación de la energía cinética turbulenta. Las micro escalas y macro escalas están relacionados con el número de Reynolds, donde el subíndice 1 corresponde a macro escala y el subíndice 2 a micro escalas, como se muestra a continuación:

Definiendo las dimensiones del dominio a analizar (riser) es posible estimar los valores de las dimensiones de las pequeñas escalas de turbulencia. Aquí es necesario comparar el tamaño de las menores escalas con el diámetro de las partículas. Si una partícula posee un tamaño menor que las escalas de Kolmogorov, esta partícula sufre sólo efectos difusivos; al encontrarse con un vórtice, la tendencia será seguir el camino del vórtice y formar aglomerados [7], [24], [25].

Para la determinar el tamaño de la malla (dx) se propone un algoritmo mostrado en la Figura 5, se recomienda que sea proporcional al tamaño de los aglomerados, de 8 a 40 diámetros de partícula, debido a que los cluster poseen en medía estos diámetros característicos [26], [27]. Cuando el tamaño de la malla orden de magnitud del diámetro de partícula, la simulación puede ser considerada como una simulación directa, sin importar que sea mayor que la menor escala longitud de la turbulencia. Esta noción tiene una importancia fundamental en la definición de refino de la malla, para una concepción de dimensiones que no viole la condición de continuidad, pues la solución de las ecuaciones capta variaciones detalladas de una única partícula y si de un conjunto de partículas. Por esta razón, solo es posible describir meso-escalas turbulentas (cluster y strands) utilizando LES.

MODELO MATEMÁTICO

Para aplicar la simulación de grandes escalas (LES) en flujos de dos fases, es importante definir el método apropiado para describir la influencia de la segunda fase en el flujo. Por ejemplo, en el caso de los flujos de partículas diluidas, en algunos casos, utilizando el método de Euler y Lagrange, en el que el flujo de gas se resuelve considerando como un medio continuo (euleriano) y para el arrastre de partículas individual, se utiliza el enfoque de Lagrange. En este trabajo, optó por adoptar un enfoque de Euler-Euler debido a que este enfoque considera el gas y el catalizador como sistemas continuos y medios interpenetrantes. En otras palabras, las diferentes fases pueden ocupar la misma posición en el espacio, introduciendo el concepto de fracción volumétrica, en el conjunto de variables. Las ecuaciones que describen las fases se muestran a continuación:

Figura 5. Algoritmo para determinar el tamaño de malla.

Ecuación de continuidad

Donde j, ρ y U son la fracción en volumen, densidad y el vector de velocidad para cada fase, respectivamente. Los subíndices g y s indican las fases de gas y partículas sólidas, respectivamente.

Ecuación de cantidad de movimiento

P y g son la presión del fluido y la aceleración de la gravedad. β es el coeficiente de descarga entre las fases

Tensores

Presión de la fase sólida [28]




, ,

El coeficiente de arrastre en la interface gas-sólido [29]

Filtrado de las Ecuaciones de Conservación

La metodología LES es un enfoque multi-escala en la dinámica de fluidos, basado en la separación por filtración, de las escalas pequeñas y grandes del flujo turbulento. LES es una operación de filtrado de las ecuaciones de momento en el espacio físico, se introduce para separar formalmente el flujo de las escalas resueltas y modeladas. Las grandes escalas de movimiento se simulan directamente, mientras que las escalas más pequeñas -escalas disipativas- se modelan. Todas las variables de campo se descomponen en componentes resueltas y no resueltas (el modelo sub-malla), utilizando una descomposición de Reynolds. Para el caso de los modelos RANS (Reynolds-Averaged Navier–Stokes) el espectro turbulento está completamente modelado, por lo tanto, el costo computacional es inferior al de LES.

Leonard [30] fue el primero en utilizar el término Large Eddy Simulation, también introdujo la idea de filtración, como una operación formal de convolución en el campo de velocidades, y dio el primer método formulación general. Las ecuaciones resultantes de filtrado gobiernan la dinámica de los vórtices mayores. Una variable filtrada se indica mediante una barra en la parte superior y se establece matemáticamente como:

Donde D es el dominio de fluido y G es la función de filtro que determina la escala de los vórtices resueltos. La parte sin resolver φ de la variable está definida por:

En LES no se lleva a cabo un promedio con el tiempo, las variables filtradas son funciones del espacio y tiempo. Contrariamente al modelo RANS 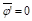y para LES [31]. La discretización de los volúmenes de control prevé implícitamente la operación de filtrado:

Donde V es el control de volumen. La función de filtro 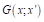el filtro Gaussiano está dada por

3.4 Modelo de sub-malla Smagorinsky

Para modelar las escalas de turbulencia es necesario un modelo sub-malla, que no puedan ser resueltas por la discretización de la malla; se utilizó un modelo sub-malla para la corrección de las viscosidades efectivas basadas en Smagorinsky [19]. Este modelo supone que la viscosidad es una función de la velocidad de deformación y los parámetros asociados con la frecuencia de corte (tamaño de la malla).

Donde l es la longitud de la escala (típicamente el tamaño de malla) y q_sm es la velocidad. Basado en un modelo de mezcla de Prandtl, la escala de velocidades está representado por los gradientes de velocidad filtrada:

Generando el modelo Smagorinsky para la viscosidad:

Donde C_S es la constante Smagorinsky. Dicho valor constante para la turbulencia isotrópica, con un rango de espectro de inercial.

El valor C_S puede cambiar en función del tipo de flujo y la calidad de la malla. Este valor está en el rintervalo de 0,065 a 0,25. A menudo, el valor de 0,1 se utiliza como el valor por defecto, con resultados favorables para la mayoría del flujo. El coeficiente C_S, sin embargo, no es una constante universal, esta podría ser la debilidad del modelo, además de requerir funciones de amortiguación cerca de las paredes.

El filtro característico se toma como el tamaño de malla local:

CONDICIONES Y PARÁMETROS DE LA MALLA

La relación de escalas turbulentas fue determinada utilizando las propiedades y dimensiones de las escalas más grandes a partir de la geometría de la riser. Esto es, por ejemplo:

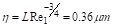
El tamaño de la escala menor, es menor que el tamaño de partícula (55 μm) que se utiliza para determinar el tamaño de la malla, como fue discutido anteriormente. La eficacia de la malla está representada por diferentes parámetros. La Tabla 1 muestra los valores característicos del determinante de la matriz jacobina y el ángulo interno mínimo de las caras del elemento de la malla creada.

Tabla 1.Parámetros de calidad de la malla.

Parámetro	Malla
Número de Volúmenes de control	100000
D¤dx	~ 0.05
dx¤dp	15
Determinante de la matriz Jacobina	> 0.5
Angulo Mínimo	> 50°

Las velocidades superficiales de gas utilizadas en los experimentos fueron de 0,36 y 1,42 m/s a temperatura ambiente (Tabla 1). Los estudios de caso se llevaron a cabo utilizando el software CFX® 16. Las simulaciones se realizaron en estado dinámico, el criterio de estabilidad considerado fue un valor promedio del número de Courant (Co) cercano a la unidad. Además, se utilizó un tiempo de paso constante para mejorar la estabilidad numérica durante la ejecución de cada una de las simulaciones.

El reactor a escala de laboratorio de 1 m de altura y 0,032 m de diámetro interno [32], fue simulado con un paso de tiempo de 0,001 s y se validó comparando con los datos experimentales, para las dos velocidades; inicialmente se tenía una altura de lecho de catalizador de 5cm. Las simulaciones fueron realizadas utilizando 4 a 8 procesadores Intel Xeon con 2,93 GHz y 16 núcleos HT. Las condiciones de la simulación se muestran en la Tabla 2 y en la Figura describe la malla utilizada.

Tabla 2. Condiciones de Frontera

Entrada	Velocidad de Gas = 0,36 y 1,42 m/s
Salida	Opening = presión atmosférica
Pared	Particulas = free slip and No slip
Pared	Gas = no slip
Altura Inicial	Altura de catalizador = 0,05 m
Partícula	60 μm; 1600 kg/m³

Diferentes simulaciones en la literatura [33], [34] mostraron que lograron una simulación precisa usando una relación D¤dx £ 0.25 para el esquema espacial de segundo orden; además razón D¤dx < 0.5 para la resolución de sexto orden; por lo tanto, los valores de relaciones de escalas D¤dx son presentados en la en la Tabla 1 coherentes con los reportados en la literatura.

Samuelberg-frente

Figura 6. Vistas de las mallas utilizadas.

Inicialmente, los sólidos en el Riser son forzados a fluir en la dirección ascendente de una manera similar al flujo pistón; cuando el lecho de sólidos comienza a expandirse, se observa una alta concentración de partículas sólidas en el centro del tubo y cerca de las paredes (Figura ), esto como resultado de una contracción de los sólidos cuando son arrastrados por el gas, característico de los lechos pre-fluidizados.

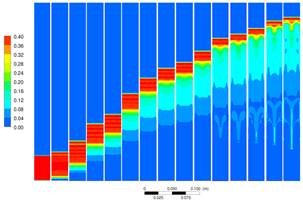
Figura 7. Evolución inicial de la concentración de sólidos en el lecho en los primeros instantmes.

La Figura muestra los perfiles de velocidad de las partículas sólidas, para tres alturas en el lecho y para las velocidades de gas superficial de 1,42 y 0,36 m s^-1, encontrándose gran similitud con los resultados presentados por Miller y Gidaspow [17], altas concentraciones de sólidos ascendiendo por el centro del cilindro y descendiendo por las paredes. Fue posible describir de forma adecuada el comportamiento descendente de las partículas, pero se observa que los perfiles de las simulaciones sobrestiman los valores experimentales en el centro; esto se debe a que el flujo, aún no se encontraba completamente desarrollado en los experimentos; no obstante, se describe el comportamiento core-annulus tal como se observa en la Figura , tal vez lo más complejo de simular en un flujo gas-sólido.

Se compararon las simulaciones realizadas por Hodapp [35], el cual utilizó una malla con aproximadamente 280000 volúmenes de control y teoría cinética granular para describir el sólido.

Figura 8. Comparación del Perfil de velocidad de partículas de Miller y Gidaspow (A)[17], datos experimentales y simulación realizada (B).

Cada simulación requirió dos meses aproximadamente para simular 15 segundos de tiempo real. En éste trabajo fue posible reducir el tiempo de simulación en un tercio, para el mismo número de procesadores. Además, se redujo el número de volúmenes para 100000 utilizando la discretización casi-uniforme.

La condición No-Slip para el sistema gas-sólido representó el comportamiento del sistema cerca de la pared. Aunque las simulaciones hechas con la condición Free-Slip presentan comportamiento y perfiles similares pero no representó el comportamiento core annulus. No se observó una diferencia significativa en el tiempo de simulación de las dos condiciones.

El enfoque LES utilizando geometrías casi uniformes ayudó en la mejora del tiempo de cómputo y en el refinado de la malla, al obtenerse mallas de menor tamaño. Para el sistema de dos fases no es necesario realizar refino cerca de las paredes del riser, esto produce inestabilidad numérica. Es necesario invertir el tiempo suficiente en el diseño de la distribución de los volúmenes de control de la malla, de manera que sean lo más uniformes en la medida de lo posible.

CONCLUSIONES

La metodología propuesta para la construcción de la malla casi uniforme, basada en la relación de escalas, beneficia en gran medida la eficiencia en las simulaciones ya que fue posible disminuir en tiempo computacional. Es importante determinar hasta qué punto la industria está interesada en describir las estructuras de meso escalas, desde el punto de vista físico, las micro escalas de la turbulencia de un gas están en el orden de magnitud de Angstrom y para las partículas sólidas están en el orden de magnitud de micra. Es difícil resolver las micro escalas de un sistema de partículas y aún imposible resolver para un sistema gaseoso. Por este motivo, actualmente sólo es posible resolver y describir meso escalas de turbulencia caracterizadas en el caso del flujo de gas-sólido por cluster y strands. LES tuvo sus orígenes en estudios atmosféricos, caracterizados por flujos gaseosos sobre una superficie sólida, en este caso se presentan pequeños vórtices cerca de la superficie, es por esta razón que se recomienda discretizar finamente cerca de la pared. Sin embargo, en un flujo gas-sólido en lecho fluidizado, estos

pequeños vórtices están presentes en todo el dominio de control. La metodología LES fué adaptada a las simulaciones de dos fases, encontrando resultados coherentes con el comportamiento core-annulus de los lechos fluidizados. Cabe resaltar que LES es dependiente del tamaño de la malla, por lo tanto es necesario invertir tiempo de diseño de las mismas de tal forma que no sea necesario refinar solo en la pared.

REFERENCIAS

[1] M. Thakkar, J. P. Makwana, P. Mohanty, M. Shah, and V. Singh, “In bed catalytic tar reduction in the autothermal fluidized bed gasification of rice husk: Extraction of silica, energy and cost analysis,” Industrial Crops and Products, vol. 87, pp. 324–332, Sep. 2016.

[2] M. M. Bello, A. A. Abdul Raman, and M. Purushothaman, “Applications of fluidized bed reactor in wastewater treatment – A review of the major design and operational parameters,” Journal of Cleaner Production, Jan, 2016.

[3] A. G. Oblad, “The Contributions of Eugene J. Houdry to the Development of Catalytic Cracking,” in Heterogeneous Catalysis, vol. 222, 0 vols., American Chemical Society, 1983, pp. 61–75.

[4] Z. Wang, “Houdry Cracking Process,” in Comprehensive Organic Name Reactions and Reagents, John Wiley & Sons, Inc., 2010.

[5] D. Y. P. B, S. A. D. S, and P. J. R. G, “Determinación de la corrosión en un Sistema CO2-H2S-Salmuera-Acero api 5L grado X65, utilizando un Electrodo de Cilindro Rotatorio,” Rev. UIS Ing., vol. 9, no. 2, pp. 219–225, 2010.

[6] F. J. V. Antwerpen, “Thermofor Catalytic Cracking,” Ind. Eng. Chem., vol. 36, no. 8, pp. 694–698, Aug. 1944.

[7] G. González, N. P. Jiménez, and O. F. Salazar, “Fluid Dynamics of Gas-Solid Fluidized Beds,” in Advanced Fluid Dynamics, InTech, 2012.

[8] L. Mleczko, “Fluidized bed chemical reactors – Old and new applications,” Fluidization XV, May 2016.

[9] J. R. Grace, “Fluidized-bed catalytic reactors,” in Multiphase Catalytic Reactors, Z. I. Önsan and A. K. Avci, Eds. John Wiley & Sons, Inc., 2016, pp. 80–94.

[10] J. Ancheyta, Modeling of Processes and Reactors for Upgrading of Heavy Petroleum. CRC Press, 2013.

[11] K. Agrawal, P. N. Loezos, M. Syamlal, and S. Sundaresan, “The role of meso-scale structures in rapid gas–solid flows,” Journal of Fluid Mechanics, vol. 445, pp. 151–185, 2001.

[12] Wen-Ching Yang, Ed., Handbook of Fluidization and Fluid-Particle Systems. CRC Press, 2003.

[13] H. Weinstein, M. Shao, and M. Schnitzlein, “Radial variation in solid density in high velocity fluidization,” 1986.

[14] D. Geldart, Gas fluidization technology. Chichester, New York: Wiley, 1986.

[15] M. J. Rhodes and D. Geldart, “The upward flow of gas/solid suspensions. I: A model for the circulating fluidized bed incorporating dual level gas entry into the riser,” Chemical engineering research & design, vol. 67, no. 1, pp. 20–29, 1989.

[16] P. A. Galtier, R. J. Pontier, and T. E. Patureaux, “Near full-scale cold flow model for the R2R catalytic cracking process,” Fluidization VI, vol. 17, p. 24, 1989.

[17] A. Miller and D. Gidaspow, “Dense, vertical gas‐solid flow in a pipe,” AIChE Journal, vol. 38, no. 11, pp. 1801–1815, 1992.

[18] A. L. Delgado, L. C. Olmos, and S. E. Rivero, “Comparative study of the indicated cycle of a diesel engine using simulation CFD and experimental data,” Rev. UIS Ing., vol. 13, no. 1, pp. 23-31, 2014.

[19] J. Smagorinsky, “General circulation experiments with the primitive equations,” Mon. Wea. Rev., vol. 91, no. 3, pp. 99–164, 1963.

[20] D. Lilly, “The representation of small scale turbulence in numerical simulation experiments,” in IBM Scientific Computing Symposium on environmental sciences, 1967, pp. 195–210.

[21] J. W. Deardorff, “Three-dimensional numerical study of the height and mean structure of a heated planetary boundary layer,” Boundary-Layer Meteorol, vol. 7, no. 1, Aug. 1974.

[22] O. L. P. Galvis, H. R. V. Torres, and J. H. G. Mejía, “Diseño de un sistema de inyección de corriente en pozo (sicp) modelado de la tubería de producción,” Rev. UIS Ing., vol. 7, no. 1, pp. 77–86, 2008.

[23] V. Mathiesen, “An experimental and computational study of multiphase flow behavior in a circulating fluidized bed,” International Journal of Multiphase Flow, vol. 26, no. 3, pp. 387–419, Mar. 2000.

[24] A. M. Ahmed and S. Elghobashi, “On the mechanisms of modifying the structure of turbulent homogeneous shear flows by dispersed particles,” Physics of Fluids, vol. 12, p. 2906, 2000.

[25] G. Wang, G. M. Evans, and G. J. Jameson, “Experiments on the detachment of particles from bubbles in a turbulent vortex,” Powder Technology, vol. 302, pp. 196–206, Nov. 2016.

[26] Y. Igci, Arthur, S. Sundaresan, S. Pannala, and T. O’Brien, “Filtered two-fluid models for fluidized gas-particle suspensions,” AIChE Journal, vol. 54, no. 6, pp. 1431–1448, 2008.

[27] W. Holloway, S. Benyahia, C. M. Hrenya, and S. Sundaresan, “Meso-scale structures of bidisperse mixtures of particles fluidized by a gas,” Chemical Engineering Science, vol. 66, no. 19, pp. 4403–4420, Oct. 2011.

[28] M. Kashyap and D. Gidaspow, “Measurements of Dispersion Coefficients for FCC Particles in a Free Board,” Industrial & Engineering Chemistry Research, vol. 50, no. 12, pp. 7549–7565, Jun. 2011.

[29] D. Gidaspow, Multiphase flow and fluidization: continuum and kinetic theory descriptions. Boston: Academic Press, 1994.

[30] A. Leonard, “Energy Cascade in Large-Eddy Simulations of Turbulent Fluid Flows,” in Turbulent Diffusion in Environmental Pollution, Proceedings of a Symposium held at Charlottesville, vol. Volume 18, Part 1, Elsevier, 1974, pp. 237–248.

[31] S. Ghosal and P. Moin, “The Basic Equations for the Large Eddy Simulation of Turbulent Flows in Complex Geometry,” Journal of Computational Physics, vol. 118, no. 1, pp. 24–37, Apr. 1995.

[32] A. Samuelsberg and B. H. Hjertager, “An experimental and numerical study of flow patterns in a circulating fluidized bed reactor,” International Journal of Multiphase Flow, vol. 22, no. 3, pp. 575–591, Jun. 1996.

[33] B. Vreman, B. Geurts, and J. Kuerten, “Large-eddy simulation of the turbulent mixing layer,” J. Fluid Mech., vol. 339, pp. 357–390, 1997.

[34] F. K. Chow and P. Moin, “A further study of numerical errors in large-eddy simulations,” Journal of Computational Physics, vol. 184, no. 2, pp. 366–380, Jan. 2003.

[35] M. J. Hodapp, “Modelagem e simulação de um leito fluidizado : um estudo comparativo,” Dissertação de Mestrado, Universidade Estadual de Campinas, 2009.

U_s = 0,36 m/s	U_s = 1,42 m/s
		0.48 m
		0.32 m
		0.16 m

Large Eddy Simulation (LES) Aplicado a un lecho fluidizado gas – sólido. Parte I:

Reactor a escala de laboratorio

Large Eddy Simulation of Gas – Solid fluidized bed. Part I:

The laboratorial scale reactor

RESUMEN

ABSTRACT