Simulación de la
interacción entre fracturas hidráulicas y fracturas naturales con aplicación de
daño continuo
Simulation of the
interaction between hydraulic fractures and natural fractures with application
of continuum damage
Anny Zambrano-Luna1, Germán González-Silva 2, Yair Quintero-Peña3
1Grupo de investigación de Estabilidad
de Pozos, Escuela de Ingeniería de Petróleos, Universidad Industrial de
Santander, Colombia. Email: anny.zambrano@correo.uis.edu.co
Grupo
de Modelamiento de Hidrocarburos, Escuela de Ingeniería de Petróleos,
Universidad Industrial de Santander, Colombia. Email: germangs@uis.edu.co
Grupo
de investigación de Estabilidad de Pozos, Escuela de Ingeniería de Petróleos.
Instituto Colombiano del Petróleo, Piedecuesta, Colombia. Email:
yair.quintero@ecopetrol.com.co
RESUMEN
El concepto de daño continuo es usado para
estudiar la interacción entre fracturas hidráulicas y fracturas naturales a
través del planteamiento de un modelo, cuyo objetivo es representar el camino
de propagación y la relación entre estos dos tipos de fracturas, así como,
predecir su complejo comportamiento sin la necesidad de predefinir su dirección
como ocurre en otras aplicaciones de elementos finitos, proporcionando
resultados más consistentes con el comportamiento físico del fenómeno. El
enfoque usa simulaciones de elementos finitos a través del software Abaqus para
modelar el fracturamiento por daño o el proceso de fracturamiento por
propagación de daño en una roca. El modelado del fenómeno se desarrolla en dos
dimensiones (2D) de manera que la fractura será representada por una línea y el
frente de fractura por un punto. Se considera comportamiento constitutivo
no-lineal, deformación finita, deformación dependiente del tiempo, deformación
hardening y softening, y deformación basada en la evolución del daño en
compresión y tensión.
PALABRAS
CLAVE: Red de
fractura compleja; daño continuo; fracturas hidráulicas; fracturas naturales;
rigidez.
ABSTRACT
The continuum damage concept is used to study the
interaction between hydraulic fractures and natural fractures through a model,
whose objective is to represent the path of propagation and the relationship
between these two types of fractures, as well as predict their complex behavior
without the need to predefine its direction as it occurs in other applications
of finite elements, providing results more consistent with the physical
behavior of the phenomenon. The approach uses finite element simulations through
Abaqus software to model damage fracturing or fracturing process by damage
propagation in a rock. The modeling the phenomenon develops in two dimensional
(2D) so that the fracture will be represented by a line and the crack front by
a point. It considers nonlinear constitutive behavior, finite strain,
time-dependent deformation, strain hardening and softening, and strain based
damage evolution in compression and tension.
KEYWORDS: Complex fracture network;
continuum damage; hydraulic fractures; natural fractures; stiffness.
INTRODUCCIÓN
La interacción entre una fractura
hidráulica y una fractura natural preexistente, parece ser el componente clave
que explique por qué algunos yacimientos exhiben un comportamiento más complejo
[1]. El diseño de fracturas hidráulicas convencionales está basado en la
suposición de que la roca es homogénea y la fractura se propaga simétricamente
en un plano perpendicular al esfuerzo mínimo, en yacimientos naturalmente
fracturados debido a la interacción con fracturas naturales, pueden propagarse
asimétricamente o en múltiples ramas o segmentos, generando una red de
fracturas complejas en el sistema [2]. Incluso, el fracturamiento hidráulico de
una formación que puede ser idealizada como homogénea, isotrópica y continua
involucra procesos complejos, no-lineales e hidromecánicos a diferentes escalas
[3].
Los yacimientos de shale gas y shale
oil en las escalas de tiempo y longitud de interés durante estimulaciones
con fracturamiento hidráulico, no pueden ser aproximadas como homogéneas,
debido a la crítica afectación resultado de la interacción entre las fracturas
hidráulicas (FH) y las fracturas naturales (FN) presentes en el medio. Esta
interacción afecta no solo la velocidad de la propagación de la FH, sino
también la estimulación del yacimiento caracterizado, donde las FN sufren
deformación inelástica (i.e. deslizamiento y apertura) [3]. De manera que, para
analizar y diseñar un tratamiento de fracturamiento hidráulico es necesario
tener herramientas capaces de simular la propagación de las fracturas en masas
rocosas discontinuas (ya fracturadas).
El modelo utilizado consiste en la
implementación del método de elementos finitos (MEF) con mecánica de daño
continuo, en el cual la fractura es representada por elementos continuos cuya
resistencia es reducida a un mínimo valor y la permeabilidad de los elementos
fisurados puede ser relacionada a la deformación o al estado de esfuerzos
correspondiente [4]; este método es capaz de simular efectos no planares o
fuera de plano [5] lo que permite observar la geometría compleja de fractura
generada y la propagación de una FH bajo condiciones geomecánicas complejas,
facilitando un verdadero análisis para el fenómeno en estudio. Para describir
la geometría de FH-FN final a través de un modelo de simulación, se presenta la
formulación de daño y el modelo constitutivo, el cual incorpora un criterio de
cedencia dependiente de la presión, una regla de flujo plástico, una regla hardening
y daño. El enfoque elimina la dirección de propagación predefinida de la FH,
característica que limita el desarrollo real de la fractura y está presente en
la mayoría de los trabajos que involucran elementos finitos en la materia;
permitiendo la evaluación de la geometría de red compleja final, usando un
software comercialmente disponible (Abaqus). La simulación fue comparada con
trabajos publicados en la literatura.
DAÑO Y DEGRADACIÓN DE LA RIGIDEZ
El modelo de daño [6], [7] incluido en
Abaqus [8], [9] aplica el concepto de módulo de deformación (E) y reducción de
rigidez, usando el parámetro de daño,  , como una aproximación adimensional de la degradación de la rigidez
para escalar el verdadero esfuerzo. En la etapa inicial,
, como una aproximación adimensional de la degradación de la rigidez
para escalar el verdadero esfuerzo. En la etapa inicial, 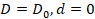 (sin degradación); y en falla,
(sin degradación); y en falla, 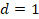 , el material es completamente dañado y el esfuerzo efectivo
disminuye a cero [10].
, el material es completamente dañado y el esfuerzo efectivo
disminuye a cero [10].
|
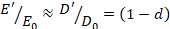
|
(1)
|
La deformación plástica incremental incluye todas las deformaciones irreversibles, así como el daño por
microfisuramiento frágil. La descomposición de la deformación en los
componentes elástico y plástico (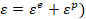 da la relación esfuerzo-deformación:
da la relación esfuerzo-deformación:
|
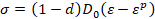
|
(2)
|
|
|
|
El concepto de esfuerzo efectivo en está
ocasión (no está relacionado con la presión de poro) es usado para degradar la
rigidez elástica, que a su vez controla la forma de la superficie de cedencia (yield
surface). El parámetro daño, evoluciona separadamente como una función de
la deformación plástica y realiza un seguimiento por separado para el daño por
tensión y compresión (Figura 1). El resultado es un material que
conserva la resistencia direccional dependiendo de cómo sea forzado.
El modelo utilizado se denomina concrete
damaged plasticity y proporciona una capacidad general para modelar
concreto y otros materiales cuasi-frágiles en todos los tipos de estructuras,
utilizando los conceptos de elasticidad y daño isotrópico combinados con plasticidad
en tensión y compresión isotrópica para representar el comportamiento
inelástico del material [9].
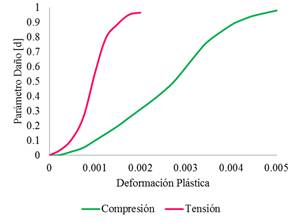
Figura 1. Daño progresivo. Fuente. [10].
Asume que las curvas de
esfuerzo-deformación uniaxial pueden ser convertidas en curvas de esfuerzo
versus deformación plástica de la forma:
|
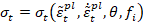
|
(3)
|
|
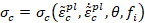
|
(4)
|
Donde los subíndices t y c hacen referencia
a tensión y compresión, respectivamente. 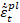 y
y 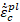 son las tasas de deformación plástica equivalente,
son las tasas de deformación plástica equivalente, 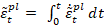 y
y 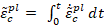 son las deformaciones plásticas equivalentes, θ es la temperatura y
son las deformaciones plásticas equivalentes, θ es la temperatura y
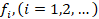 son otras variables de campo predefinidas. Se adopta la convención
de que
son otras variables de campo predefinidas. Se adopta la convención
de que 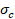 es una cantidad positiva que representa la magnitud del esfuerzo de
compresión uniaxial; es decir,
es una cantidad positiva que representa la magnitud del esfuerzo de
compresión uniaxial; es decir, 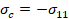 .
.
Bajo condiciones de carga uniaxial las
tasas de deformación plástica efectiva están dadas por:
|
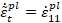
|
(5)
|
|
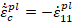
|
(6)
|
Como se muestra en la Figura 2, cuando el material es descargado
desde cualquier punto de la sección strain softening de la curva
esfuerzo-deformación, se observa que la respuesta a la descarga es el
debilitamiento: la rigidez elástica del material parece estar dañada o
degradada. La degradación de la rigidez elástica es significativamente
diferente entre las pruebas de tensión y compresión; en cualquier caso, el
efecto es más pronunciado a medida que la deformación plástica aumenta. La
respuesta a la degradación del material es caracterizada por dos variables de
daño uniaxial independientes, 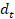 y
y 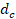 , que se supone son funciones de la de las deformaciones plásticas,
la temperatura y las variables de campo:
, que se supone son funciones de la de las deformaciones plásticas,
la temperatura y las variables de campo:
Las variables de degradación uniaxial son
funciones crecientes de las deformaciones plásticas equivalentes y, pueden
tomar valores que van desde cero, para material no dañado, a uno, para material
totalmente dañado. Si 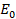 es la rigidez elástica inicial (no dañada) del material, las
relaciones esfuerzo-deformación bajo cargas de tensión y compresión uniaxial
son, respectivamente:
es la rigidez elástica inicial (no dañada) del material, las
relaciones esfuerzo-deformación bajo cargas de tensión y compresión uniaxial
son, respectivamente:
|
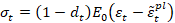
|
(9)
|
|
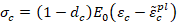
|
(10)
|
|
|
|
Adicionalmente, los esfuerzos de cohesión
uniaxial efectivos, 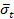 y
y 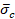 , determinan el tamaño de la superficie de
cedencia (o falla):
, determinan el tamaño de la superficie de
cedencia (o falla):
|
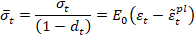
|
(11)
|
|
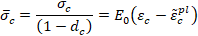
|
(12)
|
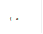
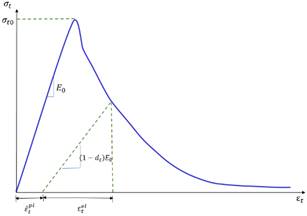
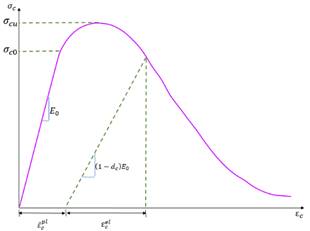
Figura 2. Respuesta del concreto a carga uniaxial en
tensión (a) y compresión (b). Fuente. [9].
MODELO CONSTITUTIVO
Incorpora un criterio de cedencia
dependiente de la presión, una regla de flujo plástico, una regla de hardening
y daño. La combinación de strain softening y daño plástico permite la
simulación de debilitamiento local extremo, donde las fracturas o zonas
fracturadas ocurren donde el material se degrada a resistencia cero. El modelo
está basado en modificaciones realizadas a la plasticidad clásica de
Mohr-Coulomb, como se describe a continuación [10].
El comienzo de cedencia (yielding)
que ocurre en la transición dúctil-frágil en rocas, es típicamente dependiente
de la presión [11], [12], [13] donde el criterio de Mohr Coulomb describe esta
relación vinculando el esfuerzo de corte y normal a través de un plano mediante
la función:
|
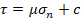
|
(13)
|
Donde 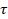 es el esfuerzo de corte,
es el esfuerzo de corte, 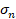 es el esfuerzo normal,
es el esfuerzo normal, 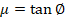 permite conocer el coeficiente de fricción y el ángulo de fricción
y,
permite conocer el coeficiente de fricción y el ángulo de fricción
y, 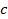 es la resistencia al
corte o cohesión.
es la resistencia al
corte o cohesión.
El criterio de Mohr Coulomb (Figura 3) asume que la falla no depende del
esfuerzo principal intermedio; sin embargo, Mogi [15], Reches y Dieterich [14] mostraron que esta suposición no es necesariamente válida en el caso general.
Asumiendo, que la superficie de cedencia (yield Surface) es totalmente
dependiente del esfuerzo principal intermedio, 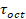 es constante para todas las rotaciones de
es constante para todas las rotaciones de 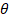 , como se indica en el criterio de Drucker Prager, donde la forma de
la superficie de cedencia es un cono que se abre con el aumento del esfuerzo
promedio.
, como se indica en el criterio de Drucker Prager, donde la forma de
la superficie de cedencia es un cono que se abre con el aumento del esfuerzo
promedio.
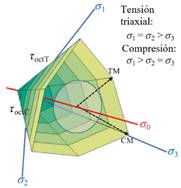
Figura 3. Superficie de cedencia de Mohr Coulomb que
muestra los meridianos de tensión y compresión (TM y CM), definidos por el
esfuerzo de corte octaédrico en tensión y compresión (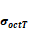 y
y 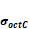 ). Fuente. [10].
). Fuente. [10].
La superficie de falla de Drucker Prager
es una variación dependiente de la presión en el criterio de Von Mises y está
dada mediante:
|
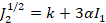
|
(14)
|
Donde 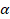 y
y 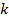 son constantes del
material, y los esfuerzos invariantes en términos de los esfuerzos principales
son constantes del
material, y los esfuerzos invariantes en términos de los esfuerzos principales 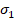 ,
, 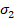 y
y 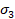 y el esfuerzo promedio
y el esfuerzo promedio 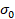 son:
son:
En el desarrollo del trabajo se utiliza la
superficie de cedencia modificada de Lubliner [6], la cual combina las
características positivas de los modelos de Mohr-Coulomb y Drucker Prager;
llamada también, superficie de cedencia del modelo Barcelona (Figura 4) [16].
La superficie Drucker Prager (ecuación 14)
ajusta dentro de la forma:
|
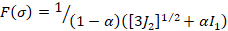
|
(18)
|
|
|
|
Añadiendo dependencia en el esfuerzo más
grande 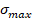 y asignando dos parámetros adicionales,
y asignando dos parámetros adicionales, 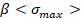 y
y 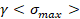 a la ecuación 18, el círculo de Drucker Prager puede ser modificado
reduciendo la dependencia del esfuerzo principal intermedio y estableciendo
meridianos de tensión y compresión. Así, la forma presentada por Lubliner [6],
Lee y Fenves [7] es:
a la ecuación 18, el círculo de Drucker Prager puede ser modificado
reduciendo la dependencia del esfuerzo principal intermedio y estableciendo
meridianos de tensión y compresión. Así, la forma presentada por Lubliner [6],
Lee y Fenves [7] es:
|
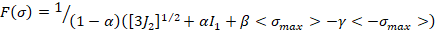
|
(19)
|
|
|
|
Donde [9]:
La resistencia a la tensión y a la
compresión uniaxial son dadas por 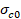 y
y 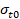 y pueden tomarse directamente desde datos experimentales.
y pueden tomarse directamente desde datos experimentales.
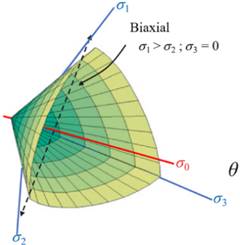
Figura 4. Superficie de cedencia Barcelona. La
curvatura es ajustada al rango entre la mínima dependencia en el esfuerzo
principal intermedio (e.g., Mohr-Coulomb) o la total de pendencia (e.g.,
Drucker Prager, un cono circular). Fuente. [10].
La resistencia de tensión biaxial 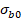 es aproximadamente 1.3% menos que la resistencia de tensión
uniaxial [7] y para
es aproximadamente 1.3% menos que la resistencia de tensión
uniaxial [7] y para 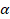 y
y 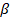 los valores típicos
están entre los rangos de
los valores típicos
están entre los rangos de 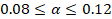 y
y 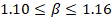 [6].
[6]. 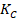 es la relación de la longitud de los meridianos de tensión y
compresión para una presión dada, es decir, controla la dependencia de
es la relación de la longitud de los meridianos de tensión y
compresión para una presión dada, es decir, controla la dependencia de 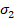 . Para
. Para 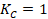 ,
, 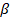 y
y 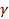 se eliminan, dejando la función original:
se eliminan, dejando la función original:
|
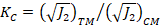 a una p dada a una p dada
|
(23)
|
Este modelo constitutivo tiene cualidades
útiles para los propósitos de las simulaciones. En primer lugar, se acomoda a
un amplio rango de tipos de rocas que eran previamente modeladas por Mohr
Coulomb o Drucker Prager. Segundo, en el modelado de nuevos tipos de rocas
desde datos experimentales, particularmente en aplicaciones de yacimiento donde
el corazonamiento es limitado, es conveniente usar falla uniaxial y datos
esfuerzo-deformación para calibraciones. Tercero, el modelo es implementado en
un software de elementos finitos comercial (Abaqus), el cual puede ser usado
para un amplio rango de problemas geológicos [10].
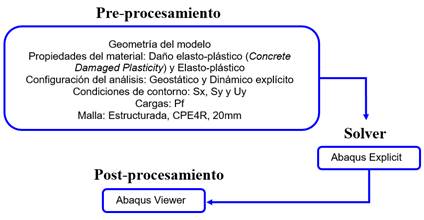
Figura 5. Procedimiento general para resolver la
aplicación a fracturamiento hidráulico. Fuente. Elaboración propia.
METODOLOGÍA
Cualquier análisis usando el software
comercial Abaqus involucra tres procedimientos principales: Pre-procesamiento,
la resolución (solver) y post-procesamiento (Figura 5), aplicable a problemas
tanto bidimensionales o tridimensionales, similar al utilizado en dinámica de
fluidos computacional [29], [30]. El proceso de simulación desarrollado se
divide en dos fases, la primera corresponde a la propagación de la FH en un
medio sin la presencia de FN y la segunda, a la propagación de una FH en
presencia de una FN con el fin de evaluar su interacción y geometría final.
Para las fases planteadas se tomó como base conceptual el trabajo realizado por
Busetti [17], enfocado en el daño y la deformación plástica de las rocas de
yacimiento. Partiendo del hecho de que las simulaciones predicen fracturas
simples a través de modelos de fracturamiento hidráulico básicos y para un
rango limitado de condiciones, Busetti, Mish y Reches [10] proponen que el
estudio realizado puede ser aplicado a yacimientos en los cuales el proceso de
fractura es mejor explicado como una red compleja o de múltiples fisuras, por
lo cual es utilizado para el modelado de la interacción de FH y FN, como se
desarrolla a continuación.
Busetti, Mish y Reches [10] utilizan un
enfoque para adaptar los datos de mecánica de rocas al modelo de daño de
elementos finitos (Figura 6) y de esta manera generar el input del
material Concrete Damaged Plasticity disponible en la librería de
Abaqus. Los datos calibrados de este material se aplican al modelo de
interacción FH-FN planteado (Tabla 1); así como, las curvas de daño
progresivo (Figura 1) y esfuerzo-deformación (Figura 7).
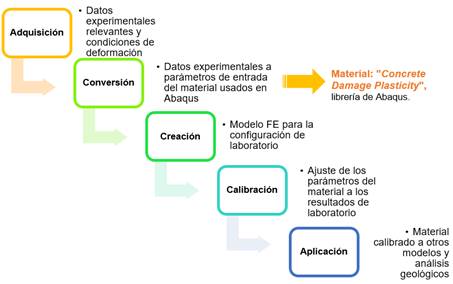
Figura 6. Enfoque para adaptar los datos de mecánica
de rocas al modelo de daño de elementos finitos en Abaqus. Fuente. [10].
Utilizando algunos de los escenarios
modelados para fracturamiento hidráulico de la investigación de Busetti, Mish y
Reches [10] (Tabla 2) se simula
la propagación de la FH con presencia de FN en el medio. El procedimiento
general (Figura 5) para la aplicación al estudio de la interacción, incluye,
una geometría con presencia de FN, cuyo espesor es 0.5 mm (10 veces mayor al
documentado por Taleghani, González y Shojaei [18]) y fracturas naturales totalmente mineralizadas. Los modelos simulados
son validados utilizando resultados experimentales publicados en la literatura.
Tabla 1. Parámetros del modelo para la reología de Berea
Sandstone, SI (mm).
|
Densidad [ton/mm3]
|
2.1E-09
|
|
Módulo de Young, E
[Mpa]
|
20200
|
|
Relación de
Poisson, v
|
0.27
|
|
Ángulo de
dilatación, ψ
|
15
|
|
Excentricidad
|
0.1
|
|
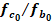 * *
|
1.16
|
|
Factor de
intensidad de esfuerzo, 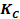
|
0.66
|
|
Regularización
Viscosa
|
0
|
* Relación entre el yield stress
equibiaxial y uniaxial compresivo (inicial).
Fuente. [17].
El modelo se enfoca en el comportamiento de
la roca bajo condiciones elasto-plásticas, daño progresivo y falla, en un
intento por simular realísticamente la deformación de la roca bajo condiciones
de esfuerzo in-situ. Los parámetros del material del modelo numérico son
derivados de las curvas de esfuerzo-deformación en tensión y comprensión de Berea
Sandstone, un análogo de roca de yacimiento común [10].
Los puntos intermedios definidos en la Figura 1 y Figura 7 fueron obtenidos por Busetti [17],
calibrando iterativamente el modelo de referencia contra los resultados de
laboratorio, de manera que el comportamiento esfuerzo-deformación se acopla
dentro de los rangos experimentales reportados para Berea Sandstone, asegurando
al mismo tiempo que las definiciones para el comportamiento postyield y
otros parámetros plásticos no conocidos fueran usados.
CASOS DE ESTUDIO
El modelo desarrollado es para propagación
vertical de un segmento de FH dentro de una formación situada lejos de los
efectos del pozo [10], cuyo fracturamiento es sensitivo al estado de esfuerzos
y genera patrones de fracturamiento que van desde fracturas rectas simples
hasta redes complejas.
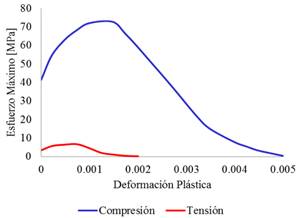
Figura 7. Curva esfuerzo-deformación post-yield.
Fuente. [10].
Tradicionalmente, las fracturas por corte y
tensión son definidas por el estado de esfuerzos en la superficie de la
fractura comenzando con los trabajos de Coulomb en 1773 y Griffith en 1921. Por
lo tanto, la aplicación de un criterio de falla relevante, por ejemplo,
criterio de Mohr Coulomb, analíticamente predice la orientación de una fractura
idealizada con respecto a un tensor de esfuerzos dado. Las
fracturas por daño son diferentes, su inicio y propagación dependen de los
campos de esfuerzo y deformación y están controladas por varios parámetros no
lineales y parcialmente independientes, por ejemplo, deformación volumétrica,
esfuerzos de tensión e historia de carga y deformación [10].
Tabla 2. Simulaciones de presurización interna.
|
Escenario
|
Estado de esfuerzos tectónicos (Mpa)
Sx - Sy
|
Distribución de la presión interna
|
Patrón de la trayectoria principal de
fractura
(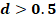 )* )*
|
Patrón de daño
(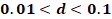 )** )**
|
|
1
|
10-50
|
Uniforme
|
Compleja, larga
|
Penetrante, bifurcada
|
|
9
|
35-50
|
Uniforme
|
Larga, recta
|
Pequeña punta de lágrima
|
* Patrón de fractura principal
interpretado como los elementos que tienen un valor de daño (d) mayor de 0.5.
** Límite de daño (d) en las gráficas de
contorno usadas para interpretar los patrones observados.
Fuente. [19].
El análisis de la propagación de la
fractura hidráulica se realizó en un modelo de dos dimensiones (2D) con las
siguientes características: La roca en estudio tiene una reología de daño
elasto-plástica que se aproxima al esfuerzo, deformación finita y falla frágil
observada experimentalmente en Berea Sandstone; la propagación de la
fractura es determinada por el estado de daño local de la roca y, como
consecuencia, la falla o fractura puede ser simulada independientemente del
proceso en la punta de la fisura (la falla macroscópica obedece al proceso de
fracturamiento por daño) y por último, la propagación
transitoria de la fractura y la detención, ruptura, ramificación y segmentación
asociadas son investigadas a través del uso de soluciones de elementos finitos
dinámicas [19], [32].
La configuración del modelo es la misma
utilizada en los trabajos de Busetti [17], Busetti, Mish, Hennings y Reches
[19]. El modelo obedece a un plane-strain 2D de dos capas con
dimensiones de 3000 mm (10 ft) de ancho y 2300 mm (7.5 ft) de alto (Figura 8). La capa inferior tiene una
reología elasto-plástica de 300 mm (1 ft) de espesor y ya se encuentra
fracturada por una fractura vertical (FV) de 300 mm de alto (1 ft) con un ancho
de 0.5 mm (0.0016 ft) en la punta y 5 mm (0.016 ft) en la base del modelo.
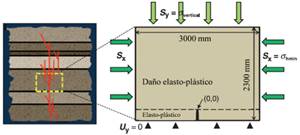
Figura 8. Escenario geológico (izquierda) y configuración del modelo de
elementos finitos (derecha) para la propagación de una fractura hidráulica
dentro de un estrato o capa sandstone. Fuente. [19].
La capa superior tiene una reología de daño
elasto-plástica que fue derivada del modelo Concrete Damaged Plasticity de
Abaqus y calibrada con datos experimentales para Berea Sandstone [10], de un espesor de 2000 mm (6.6 ft). El
modelo se carga (1) presurizando la FV en la capa inferior con lo cual se
espera que se propague hacia arriba y (2) con esfuerzos remotos o tectónicos de
régimen de falla normal (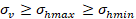 ), el modelo representa el plano
), el modelo representa el plano 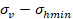 . La superficie de cedencia plástica está establecida mediante el
modelo Barcelona, el cual está basado en la plasticidad de Mohr Coulomb y usa
una adaptación de Drucker-Prager. Es importante mencionar que la resolución de
la zona equivalente de daño para una fractura es determinada por el enmallado o
distribución de la malla y que el área de localización de daño para el modelo
simulado es de la dimensión de un elemento, el cual es de 20 mm (0.065 ft).
. La superficie de cedencia plástica está establecida mediante el
modelo Barcelona, el cual está basado en la plasticidad de Mohr Coulomb y usa
una adaptación de Drucker-Prager. Es importante mencionar que la resolución de
la zona equivalente de daño para una fractura es determinada por el enmallado o
distribución de la malla y que el área de localización de daño para el modelo
simulado es de la dimensión de un elemento, el cual es de 20 mm (0.065 ft).
Las condiciones de contorno son los
esfuerzos 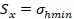 y
y 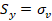 en los lados y en la parte superior del modelo para simular el
esfuerzo horizontal mínimo y el esfuerzo vertical (sobrecarga),
respectivamente, y la base está bloqueada en la dirección
en los lados y en la parte superior del modelo para simular el
esfuerzo horizontal mínimo y el esfuerzo vertical (sobrecarga),
respectivamente, y la base está bloqueada en la dirección 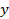 , es decir, su desplazamiento está restringido en esa dirección. La
presión dentro de la FV es aplicada para simular la inyección de fluido. En el
modelo,
, es decir, su desplazamiento está restringido en esa dirección. La
presión dentro de la FV es aplicada para simular la inyección de fluido. En el
modelo, 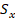 ,
, 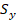 y la gravedad (Gr) son cargadas primero, seguido por un paso de
presurización, donde la presión de fractura (Pf) se incrementa hasta
y la gravedad (Gr) son cargadas primero, seguido por un paso de
presurización, donde la presión de fractura (Pf) se incrementa hasta 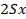 o hasta que la solución sea inestable.
o hasta que la solución sea inestable.
Para cada una de las simulaciones se
cuantifica la cantidad de daño  . A menos que se especifique lo contrario,
. A menos que se especifique lo contrario,  representa el daño combinado de tensión y compresión y es igual a
la degradación de la rigidez local, por ejemplo,
representa el daño combinado de tensión y compresión y es igual a
la degradación de la rigidez local, por ejemplo, 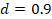 significa que el 90% de la rigidez original ha sido perdida. El
parámetro
significa que el 90% de la rigidez original ha sido perdida. El
parámetro 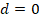 es para roca no dañada
o intacta y
es para roca no dañada
o intacta y 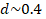 coincide con el límite de esfuerzo final y se entiende generalmente
que refleja la etapa en la que las fisuras se han unido para formar fracturas
macroscópicas, y
coincide con el límite de esfuerzo final y se entiende generalmente
que refleja la etapa en la que las fisuras se han unido para formar fracturas
macroscópicas, y 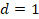 representa un daño
penetrante o una región completamente fallada con rigidez igual a cero [19].
representa un daño
penetrante o una región completamente fallada con rigidez igual a cero [19].
Fase I: Modelado del fracturamiento hidráulico
Se realiza a través de la aplicación de
esfuerzos tectónicos, seguido por la presurización interna de la fractura
vertical preexistente según las condiciones de la Tabla 2. Para los dos escenarios
seleccionados, 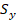 se mantiene constante y la presión interna aumenta linealmente con
el tiempo de 0 Mpa hasta
se mantiene constante y la presión interna aumenta linealmente con
el tiempo de 0 Mpa hasta 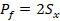 , la configuración del modelo simulado es el presentado en la Figura 8. La Pf se
incrementa a una tasa constante de 10 Mpa/s (1450 psi/s), la cual es
aproximadamente diez veces más rápida que la experimentada durante un bombeo
típico, pero permite tiempos de solución más eficientes [19]. En los modelos
simulados se toma en consideración presión uniforme en la FV. Escenarios con diferencial de esfuerzos
relativamente alto (relación grande
, la configuración del modelo simulado es el presentado en la Figura 8. La Pf se
incrementa a una tasa constante de 10 Mpa/s (1450 psi/s), la cual es
aproximadamente diez veces más rápida que la experimentada durante un bombeo
típico, pero permite tiempos de solución más eficientes [19]. En los modelos
simulados se toma en consideración presión uniforme en la FV. Escenarios con diferencial de esfuerzos
relativamente alto (relación grande 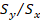 ) producen patrones largos de fractura hacia la capa superior (escenario 1 de la Tabla 2), así como ramificaciones y
segmentos extensos debido al desarrollo de sitios de acumulación asimétricos.
Los escenarios con un diferencial de esfuerzos relativamente bajo (escenario 9
de la Tabla 2) varían
significativamente, en ellos se observa propagación continua y uniforme debido
a los patrones de detención y ruptura consecutivos, así como a los corredores
de daño simétricos. Las características morfológicas comunes en las
simulaciones son presentadas en la Figura 9. Los patrones o corredores de daño
reconocidos en las figuras tienen en cuenta el indicador
) producen patrones largos de fractura hacia la capa superior (escenario 1 de la Tabla 2), así como ramificaciones y
segmentos extensos debido al desarrollo de sitios de acumulación asimétricos.
Los escenarios con un diferencial de esfuerzos relativamente bajo (escenario 9
de la Tabla 2) varían
significativamente, en ellos se observa propagación continua y uniforme debido
a los patrones de detención y ruptura consecutivos, así como a los corredores
de daño simétricos. Las características morfológicas comunes en las
simulaciones son presentadas en la Figura 9. Los patrones o corredores de daño
reconocidos en las figuras tienen en cuenta el indicador  con valores entre 0.01 y 0.1 con el fin de identificar patrones de
daño penetrantes y bifurcados en la Figura 10a
correspondiente a un patrón de trayectoria principal de fractura compleja y
larga. Para el caso de la Figura 10b es
posible notar patrones de daño en forma de pequeña punta de lagrima; al igual
que, un patrón de trayectoria principal de fractura larga y recta, concordando
con los resultados de las investigaciones de [19].
con valores entre 0.01 y 0.1 con el fin de identificar patrones de
daño penetrantes y bifurcados en la Figura 10a
correspondiente a un patrón de trayectoria principal de fractura compleja y
larga. Para el caso de la Figura 10b es
posible notar patrones de daño en forma de pequeña punta de lagrima; al igual
que, un patrón de trayectoria principal de fractura larga y recta, concordando
con los resultados de las investigaciones de [19].
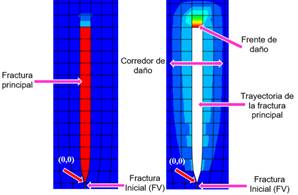
Figura 9. Características morfológicas principales.
Fuente. Elaboración propia.
La intensificación
de daño prolongado dentro de la propagación resulta en la formación de
múltiples sitios potenciales para la ramificación y segmentación (Figura 11). Se prevé que después, cuando el
fluido presurizado se propague dentro del corredor de daño (un proceso que no
es simulado en esta ocasión) esos sitios de ramificación potenciales podrían
llegar a ser ramas de crecimiento activo o permanecer como una pared de daño de
fractura, afectando de manera considerable la geometría final de propagación y
la efectividad del proceso de fracturamiento [19]. Las
ramas activas crecen en longitud y podrían eventualmente vincularse a la
trayectoria principal (Figura 11), generando mayor complejidad en
el sistema.
Las ramas y segmentos se desarrollan a
través de etapas de propagación transitoria complejas que dependen de la
configuración de carga [19]. Por ejemplo, durante las
simulaciones de presurización realizadas, las ramas y segmentos llegaron a ser
mucho más dominantes en los estados de diferencial de esfuerzos (DS) reducido (Figura 12b). Cuando se presenta un gran diferencial
de esfuerzos (Figura 12a) o un muy
bajo diferencial de esfuerzos (Figura 12b) se producen redes de fracturas
complejas, siendo más críticas las configuraciones resultado de altos DS. Por otro lado, cuando existe muy bajo diferencial de esfuerzos en la
formación y la fractura inicia su propagación, está no encuentra un camino de
propagación bien definido, por lo cual la aparición de fracturas ramificadas se
hace posible (Figura 12b), lo
que lleva a una disminución de su longitud y ancho, afectando el impacto
positivo de la FH en propagación.
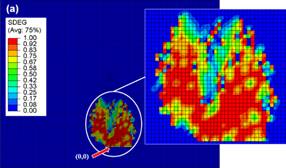
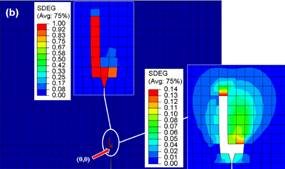
Figura 10. Presurización. Escenario 1. Sx=10Mpa,
Pf=2Sx, t=1.790s (a). Escenario 9. Sx=35Mpa, Pf=2Sx, t=7s (b). Fuente.
Elaboración propia.
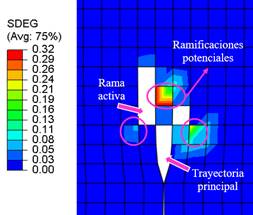
Figura 11. Presurización Escenario 1, Tabla 2. Sx=10Mpa, Pf=2Sx, t=1.780s. Rama
activa y trayectoria principal 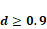 Fuente. Elaboración propia.
Fuente. Elaboración propia.
Fase II: Modelado de la interacción FH-FN
Desde la perspectiva de un yacimiento, una
fractura es una discontinuidad que se encuentra en el mismo y, es producida por
deformaciones mecánicas o procesos diagenéticos que ha sufrido la roca [20].
Figura 12. Fracturas hidráulicas formadas bajo un
rango de regímenes de esfuerzos. Fuente. Pruebas de presurización tomadas de la
Figura 10.
La Figura 13 representa la configuración para
el modelado de la interacción FH-FN y las características de ubicación espacial
de cada elemento del sistema (FN, FV, longitud y ancho, entre otras). También
se utiliza la reología de daño elasto-plástica para el material-1 y
elasto-plástica para el material-2 tal como en los trabajos de [10]. La
configuración del modelo donde se propagará la FN es el mismo utilizado para el
modelado de FH (Figura 8).
Fase II: Fracturas mineralizadas
Como su nombre lo indica, estas fracturas
son aquellas que han sido llenadas por mineralización secundaria o diagenética;
muy a menudo este material de cementación es cuarzo, carbonato o ambos y son
estudiadas por ser las más comunes en yacimientos naturalmente fracturados
(YNF) [20].
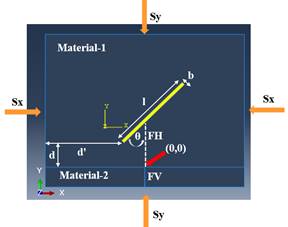
Figura 13. Modelo bidimensional de simulación. La FH
se propaga hasta lograr la interacción con una FN dispuesta a un ángulo θ.
Fuente. Elaboración propia.
Las simulaciones realizadas (Tabla 3)
demuestran la sensibilidad del patrón de geometría de fractura al diferencial
de esfuerzos y a la orientación de la FN respecto a los esfuerzos in-situ, examinando
las propiedades de las FN totalmente mineralizadas o selladas que son comunes
en formaciones tales como Barnett Shale, con el fin de evidenciar que
sirven como una trayectoria débil para el comienzo y/o desviación de la FH. Se
realizaron un total de diez simulaciones (Tabla 3) para evaluar la presencia de
FN mineralizadas, cada una de ellas con un ancho de 0.5 mm y una longitud de
120 mm. Para el análisis del diferencial de esfuerzos se tomaron los escenarios
1 y 9 de la (Tabla 2), para evaluar un alto y un bajo diferencial
respectivamente y un par de simulaciones para un diferencial igual a cero o en
estado isotrópico. La tasa de inyección para el escenario 1 es 10 Mpa/s y 35
Mpa/s para el test 9 y el isotrópico, considerando un tiempo máximo de simulación
de 2 segundos para evaluar el efecto de la Pf aplicada en la FV para cada
configuración, con ángulos de interacción de 0°, 90°, 60° y 30°. En cuanto al
material de la FN mineralizada se considera una lutita o mudstone con
una densidad de 2.0E-09 (ton/mm3), un módulo de Young de 7230 (Mpa)
y una relación de Poisson de 0.29 [21].
El inicio y propagación de las fracturas
hidráulicas es controlado principalmente por el campo de esfuerzos in-situ [22],
el cual es alterado por la presencia de discontinuidades o fracturas naturales,
configuración que ocasiona que la FH no se propague con la misma geometría o
trayectoria de propagación, dependiendo de la distribución de esfuerzos en el
medio y la presencia de FN, como puede observarse en la Figura 14 que compila
las simulaciones realizadas según la Tabla 3.
Tabla 3. Interacción con fracturas mineralizadas.
|
Caso
|
Estado de σ (Mpa)
Sx - Sy
|
Tipo de anisotropía
|
Presión de iny (Mpa, máx.)
|
θ
|
Descripción
|
|
1
|
10-50
|
Alta
|
20
|
90
|
l=120mm
d=80mm
t=1.730s
|
|
2
|
10-50
|
Alta
|
20
|
0
|
l=120mm
d=80mm
d’=1540mm
t=1.730s
|
|
3
|
10-50
|
Alta
|
20
|
60
|
l=120mm
d=20mm
t=1.730s
|
|
4
|
10-50
|
Alta
|
20
|
30
|
l=120mm
d=20mm
t=1.730s
|
|
5
|
35-50
|
Reducida
|
70
|
60
|
l=120mm
d=20mm
t=1.860s
|
|
6
|
35-50
|
Reducida
|
70
|
30
|
l=120mm
d=20mm
t=1.860s
|
|
7
|
35-35
|
Isotrópico
|
70
|
90
|
l=120mm
d=80mm
t=1.915s
|
|
8
|
35-35
|
Isotrópico
|
70
|
0
|
l=120mm
d=80mm
d’=1540mm
t=1.915s
|
|
9
|
35-35
|
Isotrópico
|
70
|
60
|
l=120mm
d=20mm
t=1.915s
|
|
10
|
35-35
|
Isotrópico
|
70
|
30
|
l=120mm
d=20mm
t=1.915s
|
Fuente. Elaboración propia.
La intersección entre fracturas es menos
probable si la dirección es paralela entre ellas (casos de comparación 2 y 8,
Tabla 3), pero se da interacción entre cuerpos cercanos, es decir, aunque no
existe contacto entre las fracturas, se altera la configuración geomecánica del
medio y las FN pueden ser reactivadas por estar dentro de la zona del proceso o
alrededor de la punta de la fractura, tal como la FN en el caso 2 y 8, donde se
evidencia reactivación. Analizando el caso donde la FN es ortogonal a la
dirección de la FH, esta última cruza la FN sin mayor oposición (casos de
comparación 1 y 7, (Tabla 3), comportamiento similar al documentado en trabajos
como el de [23] sobre la influencia de las FN en la propagación de FH.
Figura 14. Modelado de la interacción FN-FH con FN
mineralizadas. Casos de comparación del 1 al 10, Tabla 3. Fuente. Elaboración
propia.
Los casos de comparación de la Tabla 3,
muestran que la fractura en propagación cruza la FN, se queda en ella algún
tiempo (característica que puede ser observada debido al desarrollo dinámico de
cada una de las simulaciones), o en algunos casos, se queda en la FN por una
pequeña distancia y rompe de nuevo para propagarse en una dirección más
favorable mecánicamente, dependiendo del ángulo de interacción de la FN y la
FH, así como de la dirección relativa de la FN con el campo de esfuerzos;
situaciones que también pueden ser evidenciadas en investigaciones
experimentales como las realizadas por Blanton[25] , Zhou y Xue [24].
En los trabajos realizados por Wu y Olson
[26] el crecimiento de la FH es suprimido por un alto diferencial de esfuerzos,
debido principalmente a la desviación de la FH a lo largo de la FN (caso de
comparación 3, Tabla3). La Figura 15 contiene los datos del caso de
comparación 3, 5 y 9 de la Tabla 3, la cual corresponde a una interacción con
un ángulo de 60° y para el cual se grafica la afectación de un diferencial de
esfuerzos alto (40 Mpa), uno bajo (15 Mpa) y uno nulo, respectivamente. La Figura 15 denota que la FH que se propaga en
un yacimiento con un alto diferencial de esfuerzos y en presencia de FN, tiene
una penetración menor en el mismo y una apertura amplia, debido a que la
propagación de la fractura se hace más lenta cuando intercepta con la FN en el
caso de un alto diferencial de esfuerzos.
Interacciones
Las simulaciones realizadas permiten
identificar diferentes escenarios de interacción entre una FH y una FN. Los
escenarios de interacción más representativos incluyen una FH detenida en una
FN, el cruce con o sin desplazamiento, la ramificación en la intersección con
FN y la ramificación al final de una FN [27]. A través del modelado realizado
en el software comercial Abaqus y haciendo uso del material Concrete Damage
Plasticity y un análisis dinámico explícito; este tipo de interacciones
entre fracturas es posible representarlas y evaluarlas respecto al tiempo,
presentando dificultades importantes como el enmallado del medio y el gran
costo computacional que se traduce en grandes tiempos de simulación.
La Figura 16 muestra la secuencia de
propagación de la FH para el caso de comparación 3 de Tabla 3, a diferentes
tiempos de simulación, donde la Figura 16 d representa un mapa de la
interpretación de la geometría de la FH, en el que es importante señalar que
debido a que la variable daño es isotrópica, la interpretación de la dirección
del crecimiento de fractura se realiza observando el enlace entre los
elementos.
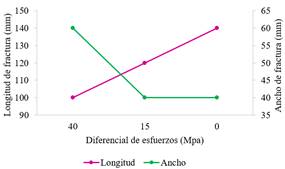
Figura 15. (a) Longitud de la fractura hidráulica y
(b) ancho para tres casos de propagación de FH con diferentes diferenciales de
esfuerzos en presencia de una FN con un θ=60°. Fuente. Elaboración propia.
Los números de la Figura 16d indican el
orden de propagación o ramificación de la FH, a través de ellos se hace posible
la identificación de interacciones como FH detenida en una FN (#2), cruce de FN
con desplazamiento (#3 y 4) y la ramificación en la intersección con una FN
(#5) y consecuente cruce.
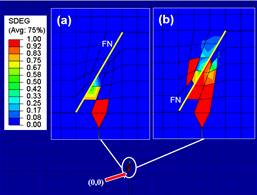
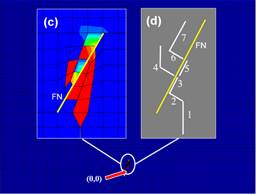
Figura 16. Secuencia de propagación de FH en
presencia de una FN mineralizada. Caso de comparación 3 de la Tabla 3. Alto
diferencial de esfuerzos y θ=60°. Fuente. Elaboración propia.
La Figura 17 representa la secuencia de
propagación para el caso de comparación 6 de la Tabla 3 donde es posible
identificar a través de la Figura 17d una FH detenida al encontrarse con la FN
(#2), el cruce de una FN sin desplazamiento (#3 y 4), la ramificación en
intersección con la FN (#6 y 8) y la ramificación al final de una FN (Figura
17c).
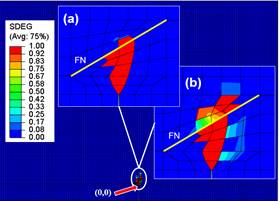
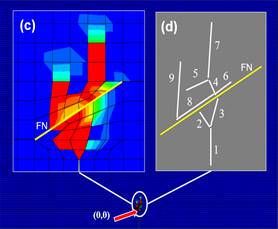
Figura 17. Secuencia de propagación de FH en
presencia de una FN mineralizada. Caso de comparación 6 de la Tabla 3. Bajo
diferencial de esfuerzos y θ=30°. Fuente. Elaboración propia.
Dependiendo de la configuración de los
casos de estudio, cada una de las interacciones puede ser observada, teniendo
en cuenta la configuración de esfuerzos, el ángulo de interacción y la Pf o
presurización del medio.
Las interacciones resultantes del modelado
realizado permiten sensibilizar parámetros como las condiciones de diferencial
de esfuerzos y el ángulo de interacción, siendo los parámetros más influyentes
en la geometría de fractura final, producto de la interacción FH-FN a través de
fracturamiento hidráulico. Dicha relación FH-FN resulta en la formación de
redes de fracturas complejas (Figura 16d y Figura 17d), a través de las cuales
podría mejorarse la productividad de la formación debido a la apertura de las
FN y al aumento del área de contacto o volumen afectado debido al
fracturamiento; en contraste con procesos de presurización que resultan poco
previsibles o exitosos debido a la coalescencia de las FN en una FH, lo que
disminuye el área de afectación o volumen de contacto. Las FN son más
sensitivas a esfuerzos que la matriz rocosa, debido a la configuración de los
mismos a su alrededor; las FN son afectadas por disturbios de esfuerzos debido
a la inyección de fluidos, resultando en apertura, cierre y reorientación de
las mismas (Figura 16 y Figura 17), influyendo en las propiedades geomecánicas
del medio y afectando principalmente la permeabilidad. Además, los efectos de
la nueva red de fractura compleja podrían verse reflejados en pérdidas de
fluido fracturante (leakoff), prematuro screen out, detención de
la propagación de fractura, formación de múltiples fracturas y presiones netas
altas [31]; incrementando la complejidad de los YNF y disminuyendo el éxito de
la operación de fracturamiento hidráulico.
Las FN totalmente mineralizadas
(simulaciones de la Tabla 3) pueden crear barreras de permeabilidad para todo
tipo de flujo, lo que a su vez podría generar pequeños compartimientos dentro
del yacimiento que pueden llevar a recuperaciones no económicas o marginales
[33]; sin embargo, bajo diferentes condiciones (Figura 14 casos 3, 4, 6 y 7)
son el inicio de una red de fracturas que lleva a un mayor volumen contactado y
por ende a un aumento en la cantidad de fluido recuperado. Si las FN de la
Figura 16 y Figura 17 no existieran el área afectada por dicha interacción no
sería posible y el éxito del tratamiento de fracturamiento hidráulico bajo
estos escenarios se reduciría, pues el objetivo principal de su aplicación en
YNF es el de contactar la mayor área posible.
Daneshy [28] atribuyo el efecto de las
fracturas preexistentes (FN) a su influencia en el campo de esfuerzos local,
situación que claramente modifica la dirección de propagación de la FH en el
medio (Figura 14). Sus experimentos al igual que el modelado realizado en esta
investigación mostraron que pequeñas fracturas, abiertas o cerradas, fueron
influenciadas localmente por la FH inducida, y fueron capaces de cambiar su
orientación general configurando una geometría de fractura más compleja.
Los escenarios de interacción FN-FH no
pueden darse de manera simultánea, pero si pueden ser observados dependiendo
del valor de la presión de inyección aplicada y las características del medio,
tales como diferencial de esfuerzos y ángulo de interacción o aproximación
(e.g. Figura 16 y Figura 17).
La identificación de los escenarios de
interacción mencionados por Weng [27] también es posible, analizando los
resultados de las simulaciones de la Tabla 3. La Figura 14 caso 1 permite
identificar bajo esas condiciones una FH detenida en la FN, al menos
momentáneamente como resultado de un valor de presión en la FH menor que el
esfuerzo normal de la FN. El cruce de una FN con o sin desplazamiento se
establece en los casos 3, 4, 5, 6, 7, 9 y 10 de la Figura 14, donde para el
cruce sin desplazamiento (casos 5, 7, 9 y 10) se cumple que la presión en el
punto de intersección excede la presión necesaria para iniciar una fractura a
lo largo de la dirección de propagación original de la FH, y para los casos con
desplazamiento la presión en algún lugar de la FN es suficientemente alta para
superar la resistencia de la fractura y romperse desde la FN en algún lugar
entre el punto de intersección y la punta de la FN. La ramificación al final de
una FN resultado de la interacción con una FH en propagación puede detallarse
en los casos 3 y 6 de la Figura 14, donde la presión en uno de los extremos de
la FN excede la presión neta requerida para comenzar la propagación desde la
punta de la FN.
CONCLUSIONES
La implementación del modelo de daño
continuo desarrollado permite identificar zonas potenciales para la
ramificación y segmentación de la fractura hidráulica generada, lo que podría
ocasionar efectos positivos tales como, la transformación en ramas de
crecimiento activo para maximizar el alcance de la fractura hidráulica creada o
efectos negativos reflejados en pérdidas de fluido fracturante o leakoff, así
como un prematuro screen out, lo que hace del modelo una herramienta valiosa
para la detección de este tipo de zonas críticas.
Las simulaciones capturan las principales
etapas de deformación de la roca, incluyendo el comienzo de inelasticidad,
strain hardening, resistencia final, strain softening y falla frágil. Debido a
que la configuración del problema se establece para capturar propagación
transitoria e inestable, con strain softening extremo, las simulaciones se
hacen muy difíciles de ejecutar; sin embargo, es lo que convierte a la
aplicación de MEF con mecánica de daño continuo en una herramienta de
predicción importante y novedosa.
El efecto de las fracturas naturales en el
campo de esfuerzos local es indiscutible, su existencia modifica las condiciones
de propagación de la fractura hidráulica y aumenta la complejidad de la
geometría final, siendo capaz de modificar la orientación original en mayor o
menor medida dependiendo de las características que describan el sistema en
estudio, por ejemplo, configuraciones sometidas a un gran diferencial de
esfuerzos y un ángulo de interacción alto, induce el cruce de las FN con o sin
desplazamiento, con menos probabilidad de alterar la trayectoria de propagación
de la FH, por lo que esta cruzará un gran número de fracturas naturales a
medida que se propaga a través del yacimiento, generando un sin número de
geometrías y aumentando su complejidad. Las diferentes interacciones analizadas
no pueden darse de manera simultánea, pero sí de manera progresiva de acuerdo
con las particularidades del medio.
El nivel de penetración en el yacimiento o
longitud de la geometría final alcanzada, al igual que el ancho de la misma,
está influenciada por el diferencial de esfuerzos, de manera que cuando los
valores del mismo son grandes, la longitud alcanzada es menor y el ancho o área
influenciada es grande comparado con niveles de diferencial de esfuerzos más
bajos, como resultado de una fuerte interacción con la FN y la propagación
sobre ella.
REFERENCIAS
[1] J. Taheri, E. Akhgarian y A. Ghaderi, “The Effect of
Hydraulic Fracture Characteristics on Production Rate in Thermal EOR Methods,”
Fuel, vol. 141, pp. 226-235, Feb. 2014.
[2] N. Potluri et al., “Effect of Natural Fractures on
Hydraulic Fracture Propagation,” SPE European Formation Damage Conference,
Sheveningen, The Netherlands: Society of Petroleum Engineers, 2005, pp. 1-6.
[3] C. Cipolla et al., “Modelling Well Performance in
Shale-Gas Reservoirs,” SPE/EAGE Reservoir Characterization and Simulation
Conference, Abu Dhabi, UAE: Society of Petroleum Engineers, 2009.
[4] M. Wangen, “Finite Element Modeling of Hydraulic
Fracturing in 3D,” Computational Geosciences, vol. 17, pp. 647-659, Ago. 2013.
[5] L. Li, C. Tang, G. Li, S, Wang, Z, Liang y Y. Zhang,
“Numerical Simulation of 3D Hydraulic Fracturing Based on an Improved
Flow-Stress-Damage Model and a Parallel FEM Technique,” Rock Mechanics and Rock
Engineering, vol. 45, pp. 801-818, Sep. 2012.
[6] D. Lubliner, “A Plastic DamageModel for Concrete,”
International Journal of Solids and Structures, vol. 25, pp. 299-326, 1989.
[7] F. Lee y G. Fenves, “Plastic Damage Model for Cyclic
Loading of Concrete Structures,” Journal of Engineering Mechanics, vol. 124,
pp. 892-900, Ago. 1998.
[8] Simulia, “Abaqus 6.11 Documentation.
Abaqus Analysis User's Manual”. [En línea]. Disponible en:
http://130.149.89.49:2080/v6.11/books/usb/default.htm
[9] Simulia, “Abaqus 6.11 Documentation.
Abaqus Theory Manual” [En línea]. Disponible en: http://130.149.89.49:2080/v6.11/books/stm/default.htm
[10] S. Busetti, K. Mish y Z. Reches, “Damage and Plastic
Deformation of Reservoirs Rcoks: Part 1. Damage Fracturing,” American
Association of Petroleum Geologists, vol. 96, pp. 1687-1709, Sep. 2012.
[11] J. Jaeger y N. Cook, “Fundamentals of Rocks Mechanics”.
London Chapman and Hall, pp. 593, 1976.
[12] W. Brace, B. Paulding y C. Scholz, “Dilatancy in the
Fracture of Crystalline Rocks,” Journal of Geophysical Research, pp. 3939-3953,
Ago. 1966.
[13] S. Murrel, “The Effect of Triaxial Stress Systems on
the Strength of Rocks at Atmosfheric Temperatures,” Geophysical Journal
International , pp. 231-281, Dic. 1965.
[14] Z. Reches y J. Dieterich, “Faulting of Rocks in Three
Dimensional Strain Fields. Failure of Rocks in Polyaxial, Servo-Control
Experiments,” Tectonophysics, vol. 96, pp. 111-132, May. 1983.
[15] K. Mogi, “Rock Fracture,” Anuual Review of Earth and
Planetary Sciences, vol. 1, pp. 63-84, May. 1973.
[16] E. Alonso, A. Gens y A. Josa, “A Constitutive Model for
Partially Saturated Soils,” Geotechnique, vol. 40, pp. 405-430, 1990.
[17] S. Busetti, “Fracturing of Layered Reservoir Rocks,”
Ph.D. dissertation, University of Oklahoma, 2009.
[18] A. Taleghani, M. Gonzalez y A. Shojaei, “Overview of
Numerical Models for Interactions between Hydraulic Fractures and Natural
Fractures: Challenges and Limitations,” Computers and Geotechnics, pp. 361-368,
2016.
[19] S. Busetti, K. Mish, P. Hennings y Z. Reches, “Damage
and Plastic Deformation of Reservoir Rocks: Part 2. Propagation of a Hydraulic
Fracture,” American Association of Petroleum Geologists, vol. 96, pp.
1711-1732, Sep. 2012.
[20] R. Nelson, Geologic Analysis of Naturally Fractured
Reservoirs, 2 ed. Houston, TX.: Gulf Prefessional Publishing, 2001.
[21] G. Shen, X. Shen y S. Wang, “Numerical and Experimental
Studies on Fracture Propagation at a Bi-material Interface and Its Application
to Hydraulic Fracturing,” American Rock Mechanics Association, Jun. 2014.
[22] D. Healy, “Hydraulic Fracturing or "Fracking":
A Short Summary of Current Knowledge and Potential Environmental Impacts,”
Science, Technology, Research & Innovation for the Environment Programme,
Jul. 2012.
[23] J. Olson y A. Dahi-Taleghani, “The Influence of Natural
Fractures on Hydraulic Fracture Propagation,” AAPG, Datapages, Inc. [En línea]. Disponible en:
http://www.searchanddiscovery.com/pdfz/documents/2010/40583olson/ndx_olson.pdf.html
[24] J. Zhou y C. Xue, “Experimental Investigation of
Fracture Interaction between Natural Fractures and Hydraulic Fracture in
Naturally Fractured Reservoirs,” SPE EUROPEC/EAGE Annual Conference and
Exhibition, Vienna, Austria: Society of Petroleum Engineers, 2011.
[25] T. Blanton, “An Experimental Study of Interaction
Between Hydraulically Induced and Pre-Existing Fractures,” SPE Unconventional
Gas Recovery Symposium, Pittsburgh, Pennsylvania: Society of Petroleum
Engineers, 1982.
[26] K. Wu y J. Olson, “Numerical Investigation of Complex
Hydraulic-Fracture Development in Naturally Fractured Reservoirs,” SPE
Hydraulic Fracturing Technology Conference, The Woodlands, Texas, USA, 2016.
[27] X. Weng, “Modeling of Complex Hydraulic Fractures in
Naturally Fractured Formation,” Journal of Unconventional Oil and Gas
Resources, vol. 9, pp. 114-135, Mar. 2015.
[28] A. Daneshy, “Hydraulic Fracture Propagation in the
Presence of Planes of Weakness,” SPE European Spring Meeting, Amsterdam,
Netherlands: Society of Petroleum Engineers, 1974.
[29] G. González, E. Matos, W. Martignoni y
M. Mori. “The Importance of 3D Mesh Generation for Large Eddy Simulation
of Gas-Solid Turbulent Flows in a Fluidized Beds,” World Academy of Science,
Engineering and Technology International Journal of Chemical and Molecular
Engineering, vol. 6, pp. 770-777, 2012.
[30] G. González, N. Prieto y O. Salazar, “Fluid Dynamics of
Gas – Solid Fluidized Beds,” en Advanced Fluid Dynamics, 1a ed. Intech, 2012, cap. 3, pp. 39-58.
[31] F. Mavares y A. Pertuz, “Cementación
de Revestidor en Flujo de Gas/Agua Presurizado Superficial no Esperado en un
Campo de Desarrollo Costa Afuera: Rio de Janeiro, Brasil,” Rev. UIS Ing.,
vol. 16, no. 2, pp. 79-92, 2017.
[32] W. Rodríguez, R. Rojas, José Yépez y
M, Pallares, “Ánalisis de Sensibilidad y de Estabilidad Numérica en el Cálculo
de Factores de Intensidad de Tensiones en un Caso de Mecánica de Fractura,” Rev.
UIS Ing, vol. 16, no. 2, pp. 151-160, 2017.
[33] D. González, C. Villabona, H. Vargas,
E. Ariza, C. Roa y C. Barajas, “Métodos para el Control e Inhibición de la
Acumulación de Depósitos Parafínicos,” Rev. UIS Ing, vol. 9, no. 2, pp.
193-206, 2010.
![]() , como una aproximación adimensional de la degradación de la rigidez
para escalar el verdadero esfuerzo. En la etapa inicial,
, como una aproximación adimensional de la degradación de la rigidez
para escalar el verdadero esfuerzo. En la etapa inicial, (sin degradación); y en falla,
, el material es completamente dañado y el esfuerzo efectivo
disminuye a cero [10].
da la relación esfuerzo-deformación:
y
son las tasas de deformación plástica equivalente,
y
son las deformaciones plásticas equivalentes, θ es la temperatura y
son otras variables de campo predefinidas. Se adopta la convención
de que
es una cantidad positiva que representa la magnitud del esfuerzo de
compresión uniaxial; es decir,
.
y
, que se supone son funciones de la de las deformaciones plásticas,
la temperatura y las variables de campo:
es la rigidez elástica inicial (no dañada) del material, las
relaciones esfuerzo-deformación bajo cargas de tensión y compresión uniaxial
son, respectivamente:
y
, determinan el tamaño de la superficie de
cedencia (o falla):
es el esfuerzo de corte,
es el esfuerzo normal,
permite conocer el coeficiente de fricción y el ángulo de fricción
y,
es la resistencia al
corte o cohesión.
es constante para todas las rotaciones de
, como se indica en el criterio de Drucker Prager, donde la forma de
la superficie de cedencia es un cono que se abre con el aumento del esfuerzo
promedio.
y
). Fuente. [10].
y
son constantes del
material, y los esfuerzos invariantes en términos de los esfuerzos principales
,
y
y el esfuerzo promedio
son:
y asignando dos parámetros adicionales,
y
a la ecuación 18, el círculo de Drucker Prager puede ser modificado
reduciendo la dependencia del esfuerzo principal intermedio y estableciendo
meridianos de tensión y compresión. Así, la forma presentada por Lubliner [6],
Lee y Fenves [7] es:
y
y pueden tomarse directamente desde datos experimentales.
es aproximadamente 1.3% menos que la resistencia de tensión
uniaxial [7] y para
y
los valores típicos
están entre los rangos de
y
[6].
es la relación de la longitud de los meridianos de tensión y
compresión para una presión dada, es decir, controla la dependencia de
. Para
,
y
se eliminan, dejando la función original: