17

INTRODUCCIÓN

Descripción del proceso

El proceso de Melt Spinning obtuvo gran difusión para la producción de materiales amorfos desde los años ´80. Estos materiales, obtenidos en forma de cintas de pequeños espesores poseen capacidades magnéticas incrementadas [3; 4]. Utilizando aleaciones amorfas, entre ellas las de Fe₇₈B₁₃Si₉(%at) para núcleos de transformadores eléctricos se logra disminuir las pérdidas en vacío hasta un 80 % [3; 5] en comparación con las de los núcleos construidos con chapas de FeSi de grano orientado, utilizadas normalmente en estos dispositivos.

El proceso de Melt Spinning consiste en la conformación de una fina lámina de aleación metálica sobre una superficie plana. En este proceso, un chorro (jet) de metal líquido es expulsado por sobrepresión de un gas inerte a través de una boquilla para luego impactar sobre la superficie de una rueda de cobre giratoria para, de esta manera, formar una capa delgada de material fundido que solidifica rápidamente como una cinta continua que luego es colectada y enrrollada. De acuerdo a la distancia que existe entre la boquilla y la rueda giratoria (Gap), se determinan los procesos de: Chill Block Melt Spinning (CBMS) y Planar Flow Casting (PFC) [6]. En el CBMS, el jet de metal líquido es expulsado a través de una boquilla con un Gap >1 mm. En el PFC, en cambio, el Gap es inferior a 1 mm.

Metodología para la obtención del producto

Partiendo de la aleación estipulada se genera un lingote de aleación madre de Fe₇₈B₁₃Si₉ (%at), obtenida a partir de ferroaleaciones comerciales [7]. Luego el lingote es triturado en partículas de un tamaño medio de aproximadamente 5 mm, y estas se introducen posteriormente en el interior de un tubo de cuarzo de 10 mm de diámetro y 1,5 mm de espesor que funciona como crisol para el proceso de obtención de la cinta. El tubo de cuarzo posee en su parte inferior una boquilla de Nitruro de Boro con un orificio de Diámetro (Z) en su centro, por donde luego de calentada, por encima de la temperatura de fusión, se eyecta la aleación en estado líquido mediante una sobrepresión controlada de gas inherte.

Parámetros del proceso productivo.

El crisol se posiciona con un Gap de 3mm constante en la configuración tipo CBMS, y con una bobina de cobre refrigerado por agua conectada a un horno de inducción se calienta la aleación sobre el punto de fusión (~1300 °C). En estas condiciones, mediante la aplicación de argón a sobrepresión (2±0.3 mbar) se expulsa el material fundido a través de la boquilla. La velocidad de eyección alcanzada sobre la boquilla, permite la formación de una fina cinta sobre la rueda giratoria. De esta manera, el material producido posee estructura amorfa debido a la tasa de enfriamiento involucrada (~10⁶ K/s) [1; 8] en el proceso. La velocidad periférica de la rueda de cobre está en el orden de los 20 m/s y el diámetro de la boquilla es de Z= 0.7 mm.

(a)

(b)

(c)

Figura 1. (a) Equipo para producción de Melt Spinning. (b) Detalle del sistema crisol – rueda. (c) Cintas obtenidas: Ancho 1,4 mm - Espesor promedio 49 mm.

Determinación de la viscosidad en el proceso.

Los parametros del modelo asumidos para el material, analisis de velocidades, presiones y Numero de Biot en particular, fueros estudiados y ya discutidos en trabajos precedentes [9; 5; 11]. En el presente trabajo se hace incapié en la continuidad del modelo anteriormente propuesto, con el agregado de cambio de fase siguiendo el trabajo de Sowjanya et. al [12] que considera para valores de viscosidades mayores a 10¹⁴ kg m^-1s^-1 la aleación metálica completamente en estado sólido.

La relación entre la viscosidad del metal en función de la temperatura durante el cambio de fase se puede estimar según la ecuación (1) de Vogel-Fulcher-Tammann de acuerdo a lo reportado por Wang [8].

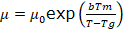(1)

Estudiando entonces el cambio de la temperatura en nuestro perfil de eyección, y considerando la dependencia funcional de la viscosidad con la temperatura, se podrá obtener la región en la que sucede el cambio de estado líquido a sólido. La Tabla 1 muestra la dependencia entre la viscosidad y la temperatura según el modelo de Vogel-Fulcher-Tammann.

Tabla 1. Viscosidad en función de la temperatura.

Temperatura		Viscosidad - µ
[°C]	[K]	kg/m s
1400	1673	1,69E-02
1350	1623	2,39E-02
1300	1573	3,53E-02
1250	1523	5,51E-02
1200	1473	9,22E-02
1150	1423	1,68E-01
1100	1373	3,41E-01
1050	1323	7,96E-01
1000	1273	2,24E+00
950	1223	8,14E+00
887	1160	7,07E+01
655	928	3,81E+14

Fuente. Vogel-Fulcher-Tammann [8].

Obtención del modelo.

Se utiliza un modelo de dos fases del tipo “Volume of Fluids” (VOF) incluido en el paquete OpenFOAM^®. A pesar de que ninguno de los dos fluidos (metal fundido y aire) puede considerarse compresible para las presiones de trabajo, se utiliza un método de resolución de naturaleza compresible. Esto permite representar los cambios de densidad en el aire por cambios de temperatura y definir un modelo termo-físico para la aleación, lo que no sería posible en las aplicaciones para flujo incompresible incluidas en el paquete OpenFOAM^®.

Se considera una aleación de conductividad térmica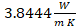, calor específico 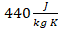y densidad 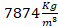como parámetros ya asumidos en modelos anteriores. Dado que el interés de este trabajo está en el cambio de varios órdenes de magnitud de la viscosidad frente a los cambios de temperatura, y a que la variación en las demás propiedades no son considerados como definitorios en el proceso de solidificación, entre las opciones de modelos viscosos que ofrece OpenFOAM^®, se selecciona un modelo polinómico. Se partió de un polinomio de grado 7 según la ecuación 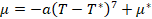(2).

(2)

Centrado en T = T^* y con raíz séptuple en ese punto, a fin de representar con una curva monótona un salto abrupto de la viscosidad en el entorno de la temperatura de cambio de fase. Utilizando rutinas OCTAVE se modificaron los valores del coeficiente 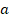, la temperatura de referencia 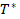y la viscosidad de referencia 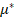buscando un polinomio de grado 7 que ajustase los valores de la Tabla 1 dentro del rango de temperaturas de 655°C a 1400°C. Los coeficientes obtenidos se muestran en la Tabla 2.

Tabla 2. Coeficientes del polinomio obtenido. C₀ refiere al término independiente y C₇ al coeficiente de grado 7.

Fuente. Elaboración propia

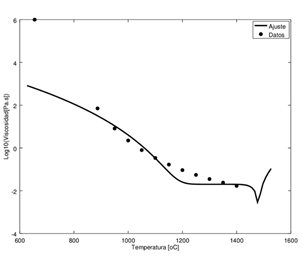
Figura 2. Polinomio ajustado a los datos obtenidos a partir de la expresión Vogel-Fulcher-Tammann.

El polinomio obtenido en la Figura 2 muestra concordancia con los valores de la Tabla 1 en el rango de 870°C a 1400°C. A fines de la simulación numérica no se considera necesario alcanzar valores de viscosidad de orden 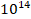kg m^-1s^-1 y se opta por considerar el material como sólido para viscosidades cercanas a 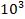kg m^-1s^-1 por lo que se desestima en la curva de ajuste el valor de viscosidad correspondiente a 655ºC. Desestimando dicho punto y evaluando el error de cada punto con el polinomio obtenido se determinan los errores en normas 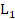, 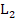y 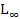expuestos en la Figura 3.

Los errores son similares en las 3 normas lo que demuestra que no existen valores demasiado alejados de la curva. La Figura 3 muestra el perfil del error en cada zona. Puede verse que en el rango entre los 900ºC y 1000ºC se sobreestima la viscosidad mientras que en el rango de 1000ºC a 1350ºC, ésta es subestimada.

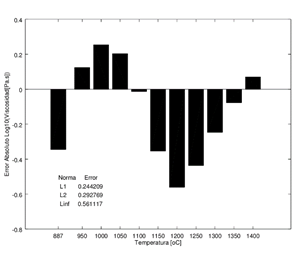
Figura 3. Errores absolutos entre los logaritmos decimales de la viscosidad de la Tabla 1 y los obtenidos con el polinomio propuesto evaluado en esas temperaturas. Se indican además las normas L₁, L₂ y 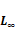del error.

Resultados de la simulación

Las Figuras 4 y 5 muestran el dominio en el entorno del punto de eyección, contraído 5 veces (factor de escala 0.2) en la dirección de avance de la cinta a fin de amplificar los fenómenos para su correcta observación.

En la Figura 4 se observa el cambio de la temperatura en el perfil conformado de cinta. La zona de mayor interés se encuentra en las isotermas próximas a los 900 °C ya que es donde se produce la solidificación del de fluido. La viscosidad observada en la Figura 5 queda determinada por el modelo matemático propuesto (la dirección horizontal del gráfico está comprimida en un factor 5 para favorecer la visualización de temperaturas y viscosidades).

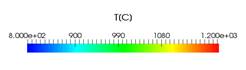
Figura 4. Representación del perfil de temperaturas en el proceso de Melt Spinning para un espesor de cinta obtenido de 40 µm.

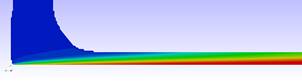
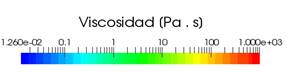
Figura 5. Representación del perfil de viscosidades en el proceso de Melt Spinning para un espesor de cinta obtenido de 40 µm.

Las Figuras 6 y 7 muestran los campos de presión en la cinta, lo que pone en evidencia la capacidad del modelo de representar el comportamiento de ambas fases. En este caso las imágenes se encuentran en la escala original.

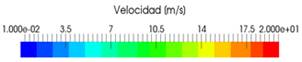
Figura 6. Representación del perfil de velocidades en el proceso de Melt Spinning para una velocidad tangencial de la rueda de 20 m/s el entorno del punto de eyección.

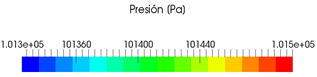
Figura 7. Representación del perfil de presiones en el proceso de Melt Spinning para una velocidad tangencial de la rueda de 20 m/s el entorno del punto de eyección.

DISCUSIÓN

Observando los valores de viscosidad de la Figura 5 se aprecia una zona de cambio de fase para temperaturas cercanas a los 950 °C. Que, de acuerdo con el modelo matemático propuesto es aproximadamente 82 kg m^-1s^-1, coincidentemente a lo reportado por otros autores para el cambio de fase [8; 5]. El polinomio propuesto por los autores de este trabajo presenta discrepancias respecto al modelo de Vogel-Fulcher-Tammann en el rango de 887ºC a 1400ºC , y éstas aumentan fuera de dicha zona. Tanto las discrepancias en el rango, como las que se encuentran fuera de éste, podrían ser eliminadas si se introdujese en la aplicación directamente la ecuación (1) propuesta por Vogel-Fulcher-Tammann. Esto será tratado en un futuro trabajo mediante la modificación del código fuente del solver. No obstante a ello, y de acuerdo al perfil de temperaturas obtenido por Wang et. al [8] y M. Bussmann et.al [13], se observan similitudes entre la Figura 6 y la Figura 4, lo que valida tambien la metodologia utilizada desde el punto de vista térmico.

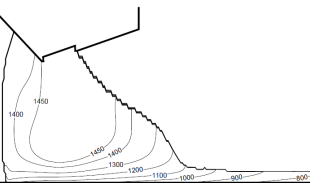
Figura 8. Perfil de isotermas en la conformación la cinta de acuerdo a M. Bussmann et.al [13].

CONCLUSIONES

En el tratamiento del modelo podemos ver que el perfil de las temperaturas está en el orden reportado en trabajos anteriores [10]. En cuanto a los valores de viscosidad podemos apreciar en la Figura 3 que el ajuste del polinomio seleccionado, resuelve razonablemente el cambio de fase impuesto en el modelado. Por otro lado, luego de la introducción del modelo térmico y viscoso como primera experimentación de simulación en OpenFOAM^®, se pueden apreciar valores de temperatura y viscosidad acordes con los obtenidos por otros autores [8; 10; 12; 13].

REFERENCIAS

[1] H. Liu, W. Chen, S. Qiu, G. Liu, "Numerical simulation of initial development offluidflow and heat transfer in planar flow casting," Metall. Mater.Trans. B vol. 40, no. 3, pp. 411–429, 2009.

[2] M. Barone, M. Pagnola, J. Useche, "Simulación con OpenFOAM® del proceso de Melt Spinning, una introducción a escala semi industrial," X Congreso Congreso Colombiano de Métodos Numéricos. Simulación en Ciencias y Aplicaciones Industriales X CCMN 2015, pp. 23-25, UTB Cartagena, Colombia, Sep., 2015.

[3] D. Muraca, J. Silveyra,M. Pagnola, V. Cremaschi, "Nanocrystals magnetic contribution to FINEMET-type soft magnetic materials with Ge addition," Journal of Magnetism and magnetic Materials, vol. 321, pp. 3640-3645, 2015.

[4] M. Pagnola,M. Malmoria,M. Baroneand H. Sirkin, "Analysis of Fe78Si9B13 (%at.) ribbons of noncommercial scrap materials produced by melt spinning equipment," Multidiscipline Modeling in Materialsand Structures, vol. 10, no. 4, pp. 511-524, 2014.

[5] Paul H. Steen, Christian Karcher,"Fluid mechanics of spin casting of metals," School of Chemical Engineering, Cornell University, Ithaca, New York 14853-5204 USA, Institute for Fluid Mechanics, Dresden University of Technology, 01062 Dresden, Germany.Kurokawa et al. - US Patent, no. 5,908,068, 1999.

[6] M. Malmoria, M. Pagnola, M. Barone, "Estudio Magnético de Cintas de FeSiB Obtenidas mediante Melt Spinning," 13^er Congreso Internacional en ciencia y Tecnología en Ciencia y Tecnología de Metalurgia y Materiales, 2013. [En línea], Disponible en: http://www.samconamet2013.misiones.gov.ar/

[7] G-X Wang and E Matthys, "Mathematical simulation of melt flow, heat transfer and non-equilibrium solidification in planar flow casting," Modelling and simulation in materials science and engineering, vol.10, no. 1, pp. 35–55, 2002.

[8] M. Sowjanya, T. Kishen Kumar Reddy,"Cooling heel features and amorphous ribbon formation duringplanar flow melt spinning process," M. Journal of Materials Processing Technology, vol. 214, pp.1861–1870, 2014.

[9] M. Bussmann,J. Mostaghimi, D.W. Kirk, and J.W. Graydon,"A Numerical Study of Steady Flow and Temperature Fields Within a Melt Spinning Puddle". Disponible en: http://lib-www.lanl.gov/la-pubs/00357001.pdf

[10] M. Barone,A.Marrugo,M. Pagnola,J. Useche, "Cambio de fase en el proceso de Melt Spinning: Análisis de capa limite y perfil térmico,” Quinto Simposio Nacional en Mecánica de Materiales y Estructuras Continuas – SMEC, 2016.

[11] M. Pagnola, M. Malmoria, M. Barone, "Biot number behaviour in the Chill Block Melt Spinning (CBMS) process," Applied Thermal Engineering, vol. 103, pp. 807–811, 2016.

RESUMEN

ABSTRACT