INTRODUCTION

The modern optimization methods allow us to find accurate enough solutions [7], with a wide variety of applications in design problems and the availability of powerful computers [8]. One of these applications is the thermal design through the Inverse Heat Transfer Problem (IHTP), which can be a effective tool in situations where other methods are incapable or inapplicable to find a solution [1]–[3]. IHTP is a methodology that consists of estimating unknown parameters involved in the physical process; it uses the information provided by a given number of measurements profiles, obtained by external sensors, (e.g., temperature or heat flux) [4][6]. One of the most important characteristics of this methodology is that the solution includes not only practical data (i.e., by experimental procedures as direct or indirect measurements) but also theoretical information about the physical process, (i.e., design and modeling) [5], [6]. Generally, this methodology needs to apply an optimization algorithm to minimize some criteria as the Ordinary Least Square Norm (OLSN).

This manuscript presents a comparative numerical study using two modern optimization algorithms, i.e., Electromagnetic Field Optimization (EFO) and Heat Transfer Search (HTS), to tackle Inverse Heat Transfer Problems (IHTPs). As an illustrative example, the parameter estimation of a rectangular microchannel heat sink was analyzed, and the results were compared with the traditional Levenberg-Marquardt (LM). Obtained data showed competitive results against traditional methods. Both methodologies (EFO and HTS) achieved estimations with errors lower than 5%, and they converged at least three times faster than LM.

This document is organized as follows: methodologies are presented in Section 2; experimental results are described in Section 3; and finally, conclusions are discussed in Section 4.

METHODS

Electromagnetic Field Optimization (EFO)

EFO was proposed by Abedinpourshotorban et al. in 2015, as a metaheuristic optimization algorithm inspired on the electromagnets’ behavior [21]. The number of design variables defines the number of electromagnets. An electromagnetic particle (), composed by electromagnets interacting with others, is a candidate solution. Three possible interaction fields, positive, negative and, neutral allow the mentioned interaction. Thus, the attraction and repulsion forces address suitable particles to the global minimal.

Pseudocode 1. Electromagnetic Field Optimization (EFO).

Require: Objective function f(x) and x_min x_s x_max,

Set N_emp, P_field, N_field, P_rate, R_rate

Ensure: Best solution to x_s

1. Initialize N_emp and Evaluate f(N_emp)

2. Sort N_emp from best to worst according to f(N_emp)

3. Classify into Positive, Negative or Neutral fields

4. if Stopping criteria are satisfied then

print Best solution x_s ← N_emp(1)

5. else

i ← 1

6. end if

7. Select a random N_emp(i) from each field

8. if rand(0, 1) < P_rate then

Set new position as selected electromagnet from positive field

9. else

Set new position by Equation (3)

Go to 12.

10. end if

11. i ← i + 1

12. if i ≤ Electromagnets then

Go to 8.

13. else

if rand(0, 1) < R_rate then

Change from N_emp with a randomly generated

N_emp(0)

else

Go to 16.

end if

14. end if

15. Evaluate f(N_emp(0))

16. if f(N_emp(0)) < f(N_emp(end)) then

Insert N_emp(0) into N_emp

Discard worst N_emp(end)

Go to 5.

17. else

Discard (N_emp(0)

Go to 5.

18. end if

Source. Own creation.

EFO Search Process: Optimization process in EFO (see Pseudocode 1) starts generating a random population . The fitness function allows to evaluate the population, which is ordered into the three possible electromagnetic fields. Best particles go to the positive field () where this portion is defined by (1),

(1)

the worst ones to the negative (). This portion of population is given by (2),

(2)

The remaining population goes to the neutral field. Then positive and negative random forces appear i.e., attraction or repulsion. A neutral electromagnetic particle is randomly generated to replace the worst particle of , which is eliminated at each iteration. This particle interacts with the forces and depending on the selected electromagnet polarity; it can be either attracted (to good solution, positive field) or repulsed (from bad solution, negative field). New position of the generated electromagnet is determined by Equation (3),

(3)

where is the new electromagnet position for design variable , is the neutral field index for an electromagnet randomly generated, and , the positive and negative field indexes, respectively. Likewise, is a random value between [0,1] and, represents a ratio of the attraction and repulsion forces (given by the golden ratio 1.6180), due to the repulsion force is weaker than attraction in about 5.0 and 10.0%. Finally, some important EFO parameters are , the probability of selecting electromagnets of the generated of the positive field without changing them. Otherwise, is the possibility of changing one electromagnet of the generated by a randomly generated electromagnet. EFO randomness plays an important role in the exploration and exploitation of searching space, promote the diversity and avoids falling in local minima.

Table 1. EFO Performance test results (five best parameters combination for Rosenbrock function).

R_rate	P_rate	P_field	N_field	N_emp
R_rate	P_rate	P_field	N_field	N_emp
0.40	0.40	0.10	0.40	100	1.27 1.62	543.4 263.9	8.86 6.33
0.30	0.10	0.05	0.40	100	3.10 4.86	464.4 334.1	4.38 2.19
0.40	0.30	0.05	0.40	50	4.97 5.86	304.6 113.8	3.91 1.13
0.20	0.10	0.05	0.50	150	6.50 5.68	218.6 52.93	3.00 0.73
0.10	0.20	0.10	0.50	100	9.44 7.20	262.0 90.60	3.75 1.55

Source. Own creation.

Table 2. Control parameters for EFO.

Method	Parameter	Possible values		Selected values
Method	Parameter	Min	Max	Selected values
EFO		50.0	Dim	100
		0.05	0.10	0.10
		0.40	0.50	0.40
		0.10	0.40	0.40
		0.10	0.40	0.40

Source. Own creation.

In Table 2, Dim represents the design variables number of the problem. If this number is less than 50, the to choose must be 50, on the contrary must be equal to the design variables number.

Heat Transfer Search (HTS)

It is a metaheuristic optimization algorithm proposed by Patel and Savsani in 2015 [22]. HTS is inspired by the fundamental thermodynamics laws, where the searching agents emulate systems interacting with other systems, and their surrounding environment exchanging energy. HTS aims at reaching the thermal equilibrium, and interactions of the systems are made of the three different heat transfer mechanisms: conduction, convection, and radiation. HTS is based on the following statement: “any system tries to reach the equilibrium with itself and its surrounding”.

Pseudocode 2. Heat Transfer Search (HTS).

Require: Objective function f(x) and x_min x_s x_max,

Set N_mol, Cd_factor, Cv_factor, Rd_factor

Ensure: Best solution to x_s

1. Initialize N_mol and Evaluate f(N_mol)

2. Generate randomly R

3. if 0.0000 ≤ R ≤ 0.3333 then

if Iteration < (G_max/Cd_factor) then

Select a solution randomly and modify by Equation (5)

else

Select a solution randomly and modify by Equation (6)

end if

Go to 7.

4. else

if 0.3333 < R ≤ 0.6667 then

if Iteration < (G_max/Rd_factor) then

Select a solution randomly and modify by Equation (10)

else

Select a solution randomly and modify by Equation (11)

end if

Go to 7.

else

Select the best solution

Calculate COS by Equation (8)

Modify solutions according to best solution by

Equation (7)

Go to 7.

end if

5. end if

6. if f(new solution) < f(best solution) then

best solution ← new solution

7. else

best solution ← best solution

8. end if

9. Replace worst solution with current solution

10. Modify duplicate solutions

11. if Stopping criteria are satisfied then

print Best solution x_s ← N_mol(iteration)

12. else

Go to 3.

13. end if

Source. Own creation.

HTS Search Process: Its process begins (see Pseudocode 2) generating a random population which is evaluated by a fitness function. If an improvement exists, the population is updated (until ). This updated can be done through three steps such as conduction, radiation, and convection (sequence steps are empirically serialized). Each one of these steps has the same probability and, to ensure an exploration and exploitation balance, the variable is used. is a random number with a uniform distribution between [0,1]; each step is linked with as shown in Equation (4),

(4)

once is generated randolmly; depending on its value, each step works as follows:

Conduction step:

The Equations (5) and (6) for this step are inspired by the Fourier law. If ,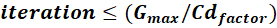

(5)

where j=1,2,3,…,n, since n is the maximum number of molecules and k is a randomly select solution from . The typical value for is 2. By the way, if ,

(6)

where is a random number uniformly distributed in [0,1].

Convection step:

The Equations (7) and (8) are inspired by Newton law,

(7)

(8)

where index represents the surrondings temperature and the mean system temperature, and is the convection stride. is the temperature change factor given by (9),

(9)

Extensive experimental trials shown that has a typical value of 10.

Radiation step:

Inspired by Stefan-Boltzmann law, it is described by Equations (10) and (11). After many trials, typical value o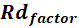f is 2. Otherwise, if ,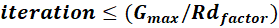

(10)

now, if ,

(11)

Equations (4) and (11) permit to calculate molecules new position to HTS algorithm for each step.

Table 3. HTS Performance test results (five best parameters combination for Rosenbrock function).

Cd	Cv	Rd	N_mol
Cd	Cv	Rd	N_mol
2.0	10	2.0	50	4.17 4.94	160.4 36.58	1.05 0.24
1.5	10	2.0	50	14.5 16.97	169.4 25.14	1.09 0.16
1.0	10	1.5	200	18.23 14.07	193.4 89.34	1.84 0.83
2.0	1.0	2.0	150	21.17 17.91	175.2 19.23	1.14 0.12
2.0	5.0	1.0	100	45.87 62.27	169.8 61.15	1.11 0.40

Source. Own creation.

Table 4. Control parameters for HTS.

Method	Parameter	Possible values		Selected values
Method	Parameter	Min	Max	Selected values
HTS		10.0	2500	50.0
		1.00	2.00	2.00
		1.00	10.0	10.0
		1.00	2.00	2.00

Source. Own creation.

In Table 1 and Table 3, represents the required iterations to converge. Similarly, those tables show the results from performance tests on Rosenbrock function to determine the best combination of parameters to ensure the convergence of the algorithms. represents the optimal value from Rosenbrock function, in this case , From these tests, the configuration parameters were selected.

Rectangular Micro-Channel Heat Sink Model

The used model for a Rectangular Micro-Channel Heat Sink was studied by Cruz et al. [19]. The Equation (12) describes the total entropy generation rate [W/K] in the RMCHS model,

(12)

Where [W] is the heat power dissipated by the electronic device, [K/W] is the equivalent thermal resistance, [K] and [K] are the surrounding and interface temperatures, respectively, [m³/s] is the volume flow rate, and [Pa] is the total pressure drop. Geometrical characteristics, material and fluid type are the design variables. The geometrical ones are,

(13)

and

(14)

where [m] represents the channel width, [m] the channel height, and [m] the wall width.

Inverse Heat Transfer Problem

This methodology has four different techniques to solve inverse problems. Levenberg-Marquardt (LM) [20], is the main method used for solving IP parameters estimation in the Technique I, according to Ozisik et al. [6]. The current inverse problem can be solved via the Technique I, which is composed of five phases depicted in Figure 1. Once the direct and inverse problem statements are mathematically defined, an efficient optimization method is proposed to minimize the Ordinary Least Squares Norm (OLSN) using the measurements profile and the process model. The procedure iterates to converge until the stopping criteria are fulfilled. The phases sequence concludes with a computational algorithm, which wraps the previous phases to obtain the complete and particular IP solution.

Figure 1. Inverse Heat Transfer Problem methodology scheme. Source. Own creation.

The direct problem (DP) requires to minimize the entropy generation of a RMCHS. The other variables are assumed as known with an adequate precision degree. The DP uses as design variables a set of parameters related to the device geometry and, it is mathematically expressed by Equation (15),

(15)

where and ^T means the transposed vector.

The inverse problem (IP) requires to estimate the parameters of a RMCHS, which produce the minimal entropy generation. The other variables are assumed as known with an adequate precision degree. Additional data are (given by an external sensor), as a function of . For all set of parameters linked to the RMCHS geometry, the IP formulation based on the OLSN is shown in Equation

(16),

(16)

where is .

The fundamental element of the iterative procedure to get a reliable solution, through the recurrent minimization of the OLSN is formally expressed by Equation (17),

(17)

where represents the squared errors sum, and gives the measured temperature in the interface between the electronic device and the heat sink. is recurrently measured by a sensor for different values of . Likewise, is the unknown parameters vector, which is defined as . is the estimated temperature by using the RMCHS model that is updated according to current parameters at each iteration . represents the number of unknown parameters, and is the number of measurements. The condition, , guarantees an adequate estimation. In the experiments, this condition is valid because of the maximum number of parameters is set to two (), and the number of measurements is one hundred (). The minimization is achieved by means of the evaluation of two recent optimization algorithms: the Electromagnetic Field Optimization (EFO) and the Heat Transfer Search (HTS), which substitute the traditional LM method.

The first criterion (Equation (18)) is the saturation condition (also known as stagnation state). The second one (Equation (19)), shows the criterion based on the statistical treatment of solution. and are the mean and the standard deviation of the solutions from the objective function. The tolerance value must be defined by the user. In our experiments, this value was defined as 1.0, arbitrarily.

(18)

(19)

The serial and the parallel strategies are proposed to look for reliable results in heat sink parameters estimation. For the former (Serial Strategy), the tests were performed (its sequence depends on the model variable influence, starting with the most sensitive). The test estimates a couple of geometric characteristics parameters . For the latter, the Parallel Strategy, also known as multi-parametric, the geometric parameters are simultaneously estimated. In the experiments, the design variables are: the channel aspect ratio , width ratio of channel to pitch . Additionally, some constraints are included to ensure algorithmic convergence. Therefore, main searching space is detailed in Equation (20).

(20)

Reference values to the thermophysical and geometric variables are shown in Table 5. The number of chosen repetitions is 50, with a maximum number of iterations predefined at 100000. For evaluation purposes, synthetic data were contaminated with additive white gaussian noise (AWGN) at ten different levels of signal-to-noise ratio, 10 dB ≤ SNR ≤ 100 dB.

Table 5. Reference and average values for thermophysical properties to aluminum and air.

Parameter	Reference value
	3.61()
	2.074
	379()
	5.45()

Source. Own creation.

EXPERIMENTAL RESULTS

A desktop iMac, Processor Intel Core^TM i5 @ 2.7-3.2 GHz, 8 GB RAM @ 1600 MHz, 64 bit with macOS Sierra was used for the experimental procedures. Table 2 and Table 3 presents the representative control parameters values used in the experiment. These data show the typical value and warranted range to obtain a fast convergence. Selected values experimentally determined from the performance output from a testing study using ten different standard benchmark functions (See Table 1, Table 3 and, Table 6).

Table 6. Standard benchmark functions and tested dimensions

Function	Dimensions
Ackley	2, 5, 10
Bird	2
Bukin #6	2
Carrom Table	2
Chichinadze	2
Goldstein-Price	2
Helical Valley	2
Plateau	2, 5, 10
Rosenbrock	2, 5, 10
Test Tube Holder	2

Source. Own creation.

The results on the Rosenbrock function (21) are shown as examples of the algorithms performances.

(21)

· Searching domain:

for .

· Global optimum:

for

when

· Dimensions: n.

Figure 2. Three-dimensional representation of Rosenbrock function. Source. Own creation.

Performance test

The convergence of the algorithms was tested with the standard benchmark functions. Figure 3 and Figure 4 show the convergence of EFO and HTS, respectively.

Imagen que contiene mapa

Descripción generada con confianza muy alta

Figure 3. EFO algorithm convergence. Source. Own creation.

Figure 4. HTS algorithm convergence. Source. Own creation.

Total entropy generation rate estimation

The estimation of the total entropy generation rate ( that was obtained compiling the individual parameters estimations. Therefore, Figure 5 shows that estimation to EFO and HTS algorithms for 50 dB of SNR. Before 0.4 of , the estimation error was fewer than 1.00%, it was a reiterative result for all the SNR levels. The cause of that result is due to the RMCHS model depends on conduction and convection heat transfer mechanisms. The convection mode is directly related to the value, when this value is near to zero, the conduction mode takes over the process and the heat transfer is almost constant because of the material body heat sink nature. Conduction mode is independent of the work substance quantity flowing through the heat sink microchannels. In this part, the estimation process can be achieved without clear complications. But the estimation in that part is not relevant because the optimal points are in another zone. Once the value increases both heat transfer modes are present and the high non-linearity is more remarkable. Thus, the estimation process shows differences regard to the reference values.

Figure 5. Estimation of (Normalized) with reference value to 50 dB of SNR. Source. Own creation.

Besides, the process was observed stable to SNR greater than 30 dB. However, estimations from EFO algorithm had relative errors of at least 112%, with quantities of noise between 10 and 20 dB, this is mainly due to high noise levels.

Estimated relative errors () were inferior to 5.00% when SNR is equals 50 dB. Relative errors was calculated by (22),

(22)

Comparative serial and parallel strategies

For inverse problems, the multi-parametric optimization is the common strategy when it is required to estimate a high quantity of parameters. Thus, the parameters estimation is made in simultaneous (or parallel), decreasing the processing time, and affecting some other parameters. However, the precision is one of the most important characteristics to be considered, i.e., it is a decisive variable between the serial strategy (above analyzed) and the multi-parametric (parallel strategy). Table 7 shows a comparison between serial and parallel strategies for each parameter. Both, EFO and HTS working in serial strategy reached estimations with relative errors smaller than 5.50% (5.47% with HTS for ) for the majority of parameters. For three over eight parameters (, , and ), the parallel strategy with EFO, produces errors between 5.50% and 11.5%. Contrarily, HTS with the same parallel strategy gives relative errors in the interval of 1.00% and 28.0%. The smallest errors were obtained for , , and independently of the chosen strategy or algorithm. Statistical analysis exhibits that standard deviations are bigger in the parallel than in the serial strategy. In other words, the reliability of a solution increases by using the serial strategy.

Table 7. Relative errors () for serial and parallel strategies for the estimation of , at 50 dB of SNR.

Strategy
Serial		Parallel
EFO	HTS	EFO	HTS
4.58	4.89	5.66	27.9
3.41	3.97	8.65	2.14

Source. Own creation.

Comparative with other Non-traditional Algorithms

For comparative purposes, similar reference patterns are used to evaluate selected methods with well-known non-traditional optimization algorithms (i.e., Unified Particle Swarm Optimization (UPSO), Simulated Annealing (SA) and Spiral Optimization (SO)). This comparison is fundamental to detect particular features of each algorithm. The experimental analysis showed that EFO gave the best results, HTS followed it for each value. Figure 6 show a comparison of relative errors of the entropy generation rate estimation at 50 dB. Therefore, EFO and HTS had best relative errors, their processing times are lower than others.

Comparative with the Traditional Algorithm

The Figure 7 presents a comparative analysis between proposed and the traditional method, which was used to estimate the unknown parameters. Results obtained from Levenberg-Marquardt method were taken as a reference to evaluate EFO and HTS results.

Figure 6. Relative errors comparative with non-traditional algorithms against reference value of for each value at 50 dB of SNR. Source. Own creation.

Experiences show that LM obtains better estimations over studied methods, but differences between them are inferior to 3.50% (e.g., for parameter using HTS). However, selected algorithms were at least three times faster than LM. The estimation precision is similar for the three compared algorithms. EFO and HTS utilized a number of iterations inferior to LM; and consequently, the number evaluations associated with the objective function is also inferior.

Figure 7. Comparison of relative errors of estimation between EFO, HTS and LM at 50 db of SNR for each parameter. Source. Own creation.

CONCLUSIONS

This paper presented a comparative numerical study using two modern optimization algorithms, i.e., Electromagnetic Field Optimization (EFO) and Heat Transfer Search (HTS), to tackle Inverse Heat Transfer Problems (IHTPs). As an illustrative example, the parameter estimation of a rectangular microchannel heat sink was analyzed, and the results were compared with the traditional Levenberg-Marquardt (LM) method. Additionally, two estimation strategies were studied: serial and parallel. Obtained data showed competitive results against traditional methods. Both methodologies (EFO and HTS) achieved estimations with errors lower than 5%, and they converged at least three times faster than LM. It was found that EFO is seven times faster than HTS. Furthermore, several differences among the two estimation strategies were noticed, i.e., parallel strategy was almost three times faster and had greater errors (between 0.10% and 5.5%) than the serial one. Specifically, the parallel strategy implemented with EFO showed smaller errors than using HTS. Moreover, the methodologies implemented in this work were compared with commonly used optimization algorithms, such as Simulated Annealing (SA), Unified Particle Swarm Optimization (UPSO) and Spiral Optimization (SO). This comparative study gave us negligible differences between their relative errors, but EFO and HTS spent at least half of time than the required by SA, UPSO and SO.

ACKNOWLEDGMENT

The authors would like to thank to the Mexican Council of Science and Technology (CONACyT) and especially, to the Engineering Division of the Campus Irapuato-Salamanca, Universidad de Guanajuato by its financial support.

REFERENCES

[1] X.-D. Wang, B. An, and J.-L. Xu, “Optimal geometric structure for nanofluid-cooled microchannel heat sink under various constraint conditions,” Energy Convers. Manag., vol. 65, pp. 528–538, 2013.

[2] Z.-H. Wang, X.-D. Wang, W.-M. Yan, Y.-Y. Duan, D.-J. Lee, and J.-L. Xu, “Multi-parameters optimization for microchannel heat sink using inverse problem method,” Int. J. Heat Mass Transf., vol. 54, no. 13, pp. 2811–2819, 2011.

[3] X.-D. Wang, B. An, L. Lin, and D.-J. Lee, “Inverse geometric optimization for geometry of nanofluid-cooled microchannel heat sink,” Appl. Therm. Eng., vol. 55, no. 1, pp. 87–94, 2013.

[4] E. Garcia, I. Amaya, R. Correa, “Algoritmos de optimización en la estimación de propiedades termodinámicas en tiempo real durante el tratamiento térmico de materiales con microondas,” Rev. UIS Ing., vol. 16, no. 2, pp. 129–140, 2017.

[5] F. D. M. Neto and A. J. da Silva Neto, An introduction to inverse problems with applications, First. Springer Science & Business Media, 2012.

[6] M. N. Ozisik, Inverse heat transfer: fundamentals and applications, First. Taylor & Francis, 2000.

[7] A. El Hami and S. Kadry, “Global optimization method for design problems,” Eng. Rev., vol. 36, no. 2, pp. 149–155, 2016.

[8] L. M. Rere, M. I. Fanany, and A. M. Arymurthy, “Metaheuristic algorithms for convolution neural network,” Comput. Intell. Neurosci., vol. 2016, 2016.

[9] R. Gielen and M. Baelmans, “Electronics Cooling System and Component Design According to the Second Law,” J. Heat Transfer, vol. 136, no. 5, pp. 40–51, 2014.

[10] R. Remsburg, Thermal design of electronic equipment, First., vol. 10. CRC press LLC, 2000.

[11] A. M. Adham, N. Mohd-Ghazali, and R. Ahmad, “Thermal and hydrodynamic analysis of microchannel heat sinks: A review,” Renew. Sustain. Energy Rev., vol. 21, pp. 614–622, 2013.

[12] D. B. Tuckerman and R. F. W. Pease, “High-performance heat sinking for VLSI,” IEEE Electron device Lett., vol. 2, no. 5, pp. 126–129, 1981.

[13] S. Baodong, W. Lifeng, L. Jianyun, and C. Heming, “Multi-objective optimization design of a micro-channel heat sink using adaptive genetic algorithm,” Int. J. Numer. Methods Heat Fluid Flow, vol. 21, no. 3, pp. 353–364, 2011.

[14] A. A. Khan, S.-M. Kim, and K.-Y. Kim, “Multi-objective optimization of an inverse trapezoidal-shaped microchannel,” Heat Transf. Eng., vol. 37, no. 6, pp. 571–580, 2016.

[15] A. Bejan, Entropy generation minimization: the method of thermodynamic optimization of finite-size systems and finite-time processes, First. CRC press LLC, 1995.

[16] A. Sciacovelli, V. Verda, and E. Sciubba, “Entropy generation analysis as a design tool—A review,” Renew. Sustain. Energy Rev., vol. 43, pp. 1167–1181, 2015.

[17] R. Gielen, F. Rogiers, Y. Joshi, and M. Baelmans, “On the use of second law based cost functions in plate fin heat sink design,” in Semiconductor Thermal Measurement and Management Symposium (SEMI-THERM), 2011 27th Annual IEEE, 2011, pp. 81–88.

[18] A. M. Adham, N. Mohd-Ghazali, and R. Ahmad, “Optimization of a rectangular microchannel heat sink using entropy generation minimization (EGM) and genetic algorithm (GA),” Arab. J. Sci. Eng., vol. 39, no. 10, pp. 7211–7222, 2014.

[19] J. M. Cruz-Duarte, A. Garcia-Perez, I. M. Amaya-Contreras, and C. R. Correa-Cely, “Designing a microchannel heat sink with colloidal coolants through the entropy generation minimisation criterion and global optimisation algorithms,” Appl. Therm. Eng., vol. 100, pp. 1052–1062, 2016.

[20] E. L. Arias, L. G. Garcia, O. Gualdrón, R. Correa, “Redes neuronales artificiales en conducción de calor multidimensional transitorio,” Rev. UIS Ing., vol. 2, no. 1, pp. 51–61, 2003.

[21] H. Abedinpourshotorban, S. M. Shamsuddin, Z. Beheshti, and D. N. A. Jawawi, “Electromagnetic field optimization: A physics-inspired metaheuristic optimization algorithm,” Swarm Evol. Comput., vol. 26, pp. 8–22, 2016.

[22] V. K. Patel and V. J. Savsani, “Heat transfer search (HTS): a novel optimization algorithm,” Inf. Sci. (Ny)., vol. 324, pp. 217–246, 2015.

ABSTRACT

RESUMEN

INTRODUCTION

METHODS

Electromagnetic Field Optimization (EFO)

Heat Transfer Search (HTS)

Conduction step:

The Equations (5) and (6) for this step are inspired by the Fourier law. If ,

Convection step:

The Equations (7) and (8) are inspired by Newton law,

Radiation step:

Inspired by Stefan-Boltzmann law, it is described by Equations (10) and (11). After many trials, typical value of is 2. Otherwise, if ,

Rectangular Micro-Channel Heat Sink Model

Inverse Heat Transfer Problem

EXPERIMENTAL RESULTS

Performance test

Total entropy generation rate estimation

Comparative serial and parallel strategies

Comparative with other Non-traditional Algorithms

Comparative with the Traditional Algorithm

CONCLUSIONS

ACKNOWLEDGMENT

REFERENCES